在上一節中,我們使用 客層一致性,也就是比較 客層群組。
或者,我們也可以只比較 成年人和少數族群的候選人。如果接受率 兩組的合格學生比例相等 機會平等: 標籤 (「符合入場資格」) 的學生 刊登廣告的機率 (不論他們屬於哪個客層群組) 。
讓我們回顧上一節的候選模型:
| 多數群組 | 少數族群 | |
|---|---|---|
| 符合資格 | 35 | 15 |
| 不符資格 | 45 | 5 |
假設許可模型接受大多數群組的 14 位候選人 未成年人中有 6 位候選人。會滿足模型的決策 等於合作對象的接受率 符合資格的少數對象為 40%
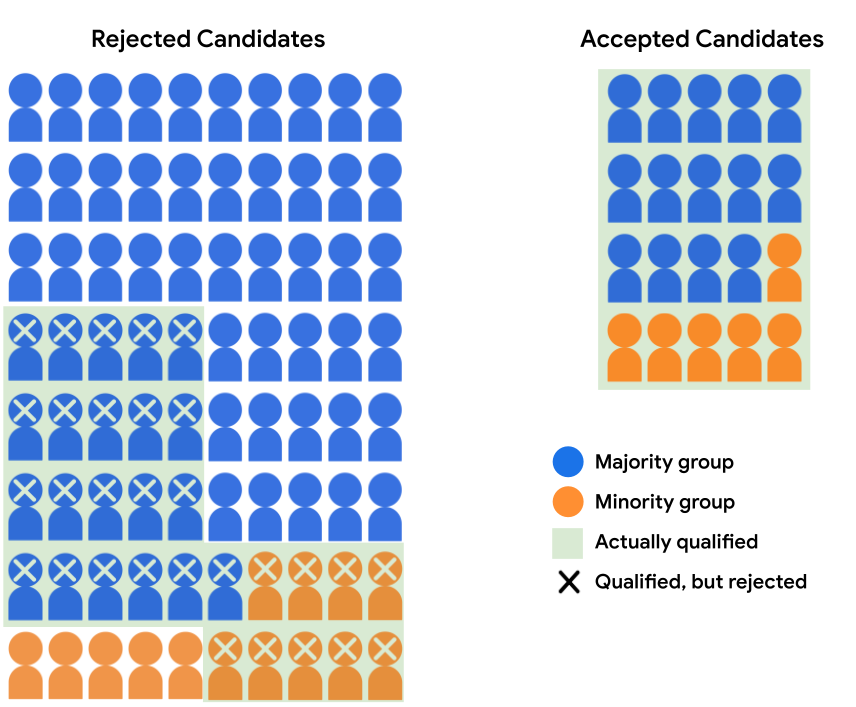
下表量化了支援遭拒和已接受的號碼 圖 4 中的候選文字。
| 多數群組 | 少數族群 | |||
|---|---|---|---|---|
| 已接受 | 已拒絕 | 已接受 | 已拒絕 | |
| 符合資格 | 14 | 21 | 6 | 9 |
| 不符資格 | 0 | 45 | 0 | 5 |
優點和缺點
機會平等的主要優點在於模型能 預測出的陽性與負面預測的比例與不同客層的差距, 前提是模型在預測偏好標籤時成效相等 (「符合入場資格」)。
圖 4 中的模型預測結果「不」符合客層一致。 多數學生的接受機會為 17.5%,且 該少數學生有 30% 的機會獲選。不過 凡是符合資格的學生,都有機會獲得 40% 的申請通過, 這個結果同樣可以看出 特定模型用途
機會平等的缺點之一,就是是專為使用設計 特別適合用到清楚的偏好標籤的情況是否同樣重要 模型預測正向類別 (「符合入學資格」) 和負面類別 (「不符合入學資格」), 建議您改用 等值勝率,會強制實施 確保兩個標籤的成功率相同
另一個機會平等的缺點是評估公平性
藉由比較客層群組的錯誤率
不一定每次都能可行例如,假設我們的入學模型資料集
不含 demographic_group 的功能,因此無法
列出符合資格的多數和少數候選人的接受率
進行比較
在下一節中,我們會探討另一個公平性指標「反事實」(counterfactual) 公平性 (可運用在客層資料不適用的情況下) 。
練習:隨堂測驗
模型的預測結果有可能同時符合兩個客層 商機的對等性和平等。
舉例來說,假設有個二元分類器 (偏好使用標籤的人員) 是正類別) 以 100 個樣本評估,結果 中顯示的混淆矩陣 客層群組 (少數與少數族群):
| 多數群組 | 少數族群 | |||
|---|---|---|---|---|
| 預測為陽性 | 預測性陰性 | 預測為陽性 | 預測性陰性 | |
| 實際為正值 | 6 | 12 | 3 | 6 |
| 實際為負值 | 10 | 36 | 6 | 21 |
|
\(\text{Positive Rate} = \frac{6+10}{6+10+12+36} = \frac{16}{64} = \text{25%}\) \(\text{True Positive Rate} = \frac{6}{6+12} = \frac{6}{18} = \text{33%}\) |
\(\text{Positive Rate} = \frac{3+6}{3+6+6+21} = \frac{9}{36} = \text{25%}\) \(\text{True Positive Rate} = \frac{3}{3+6} = \frac{3}{9} = \text{33%}\) |
|||
多數和少數族群的預測率都是正值 達到 25% 的客層門檻,並滿足客層條件,而且真陽性 (具有偏好標籤的範例百分比) 正確分類) 佔 33%,滿足商機平等
