公平性：人口均等

在评估模型预测的公平性时，我们可以使用的一种方法是 比较多数群体和少数群体的入学率。 如果两个入学率相等，模型的预测结果表明 受众特征对等： 学生被录入大学的几率不会因 受众特征群体。

假设该录取模型接受多数人的 16 位候选人 选出了 4 位来自少数族裔群体的候选人。模型的决策 即多数人和多数人均符合人口统计学特征的接受率， 少数民族候选人占 20%。

图 2. 候选人池分为两组：被拒的候选人 和已接受的候选能量塔。多数（蓝色）和少数（橙色） 的接受率为 20%。

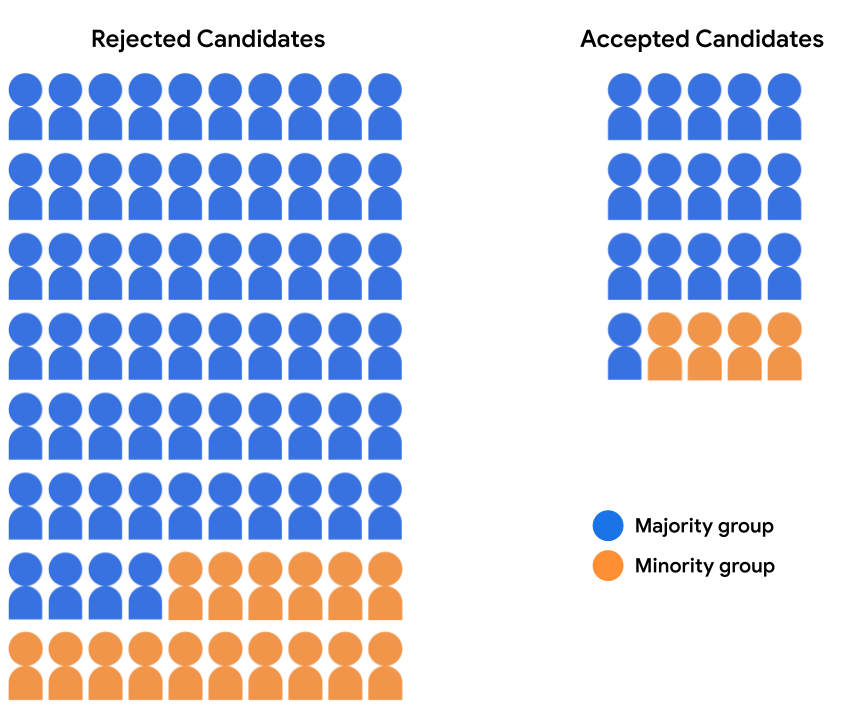
下表量化了支持被拒和已接受的 API 的数字 如图 2 所示。

	多数派	少数群体
已接受	16	4
已拒绝	64	16
接受率	20%	20%

练习：检查您的直觉

大学招生委员会正在考虑使用人口统计学平等 作为模型的公平性评估指标，需要您的指导 介绍这种方法的优缺点你能找出一个吗 优点和使用受众特征评估模型预测结果的一个缺点 对等？

您能找出特征数据存在的任何问题吗？

点击此处查看我们的回答

优点和缺点

在我们的招生示例中，人口统计对等的关键优势在于 确保多数人和少数族裔群体都有机会 与候选集中的学生群体的比例相同。 也就是说，如果申请者群体由 80% 的多数党候选人组成 拥有 20% 的少数族裔候选人，受众特征平等可以保证 在入学者中，80% 为多数群体学生，20% 为少数群体 学生。

但是，受众特征对等有一个显著的缺点： 被归类为“合格”的学生而不是“不符合条件”） 评估应如何分配 20 个入场空档。

我们再来看一下上述候选者群的构成。 不过，这次我们不仅按照受众特征群体对候选人进行分类， 还取决于模型是否将每个候选定位设置都打成了“符合条件”或 "unqualified":

图 3. “已拒绝”和“已接受”的候选人的细分数据与 但这次大多数符合条件的学生 少数民族群体以绿色阴影表示，符合条件的学生 则标有“X”在 35 个符合条件的多数群体中 有 16 名学生被录取。在这 15 名符合条件的少数族裔学生中， 有 4 项任务被接受。

下表量化了支持被拒和已接受的 API 的数字 如图 3 所示。

	多数派		少数群体
	已接受	已拒绝	已接受	已拒绝
符合条件	16	19	4	11
不符合条件	0	45	0	5

我们将以下两组数据中符合条件的学生的录取率制成表格：

$$\text{Majority acceptance rate} = \frac{\text{qualified majority students accepted}}{\text{total qualified majority students}} = \frac{16}{35} = \text{46%}$$

$$\text{Minority acceptance rate} = \frac{\text{qualified minority students accepted}}{\text{total qualified minority students}} = \frac{4}{15} = \text{27%}$$

尽管这两组的总体接受率都是 20%， 符合条件的大多数学生的录取率为 46%， 而符合条件的少数族裔学生的录取率只有 27%。

在这种情况下， （例如“符合条件”）相差很大，因此受众特征对等可能会 不是评估公平性的最佳指标。在未来 我们会介绍另一个公平性指标，即机会平等， ，后者会将这些差异考虑在内。

注意： 如果与受众特征一致， 也值得考虑，具体取决于 模型的目标以及模型所处的社会环境 使用预测。

关键术语：

• 偏见（道德/公平性）
• 受众特征对等