在上一部分中,我们使用 比较两者的总体接受率 受众特征群体。
或者,我们可以只比较合格 多数人和少数族裔群体中的候选人出席。如果接受率 两组符合条件的学生人数相等,该模型显示 机会平等: 具有首选标签(“符合入学资格”)的学生在 被录取的可能性,无论他们属于哪个受众特征群体 目标。
我们来回顾一下上一部分中的候选人池:
| 多数派 | 少数群体 | |
|---|---|---|
| 符合条件 | 35 | 15 |
| 不符合条件 | 45 | 5 |
假设招生模型接受多数群体中的 14 个候选人 和 6 位来自少数族裔群体的候选人。模型的决策满足 即合格多数人的接受率, 符合条件的少数族裔候选人的得分为 40%。
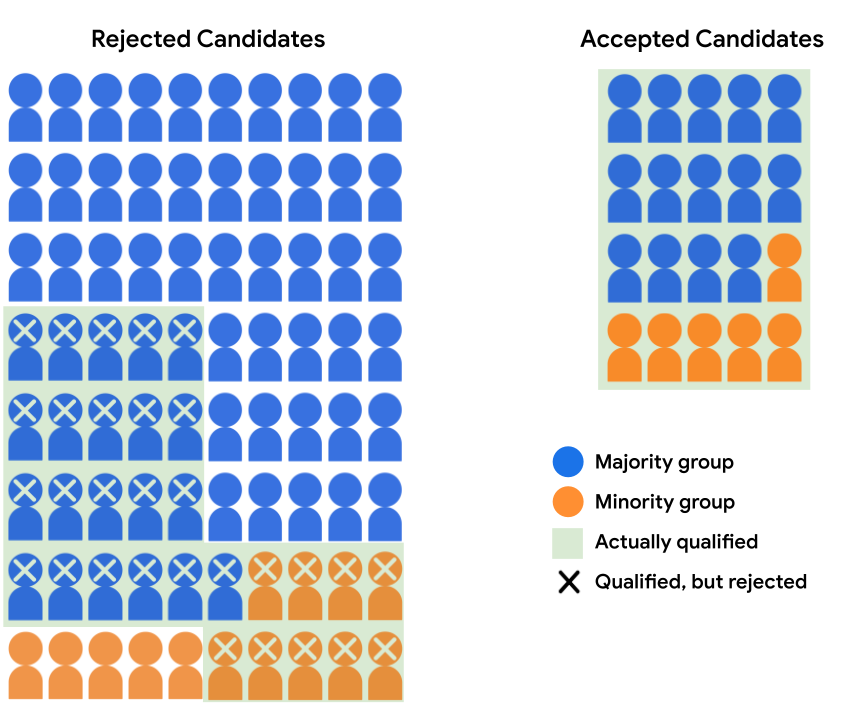
下表量化了支持被拒和已接受的 API 的数字 如图 4 所示。
| 多数派 | 少数群体 | |||
|---|---|---|---|---|
| 已接受 | 已拒绝 | 已接受 | 已拒绝 | |
| 符合条件 | 14 | 21 | 6 | 9 |
| 不符合条件 | 0 | 45 | 0 | 5 |
优点和缺点
机会平等的关键好处在于, 正向预测与负向预测的比率因受众特征群体而异, 但前提是该模型在预测首选标签方面 (“符合入场条件”)。
图 4 中的模型预测不满足受众特征一致性, 学生入学的几率为 17.5%, 少数族裔学生被录取的概率为 30%。不过, 符合条件的学生有 40% 的概率被录取 这可能是一种更公平的结果, 特定的模型用例。
机会平等的一个缺点是, 如果有明显的首选标签如果它们同样重要 模型对正类别和字词的预测性预测为正类别(“符合准入条件”) 以及负类别(“不符合入场条件”)的所有受众群体; 那么可能合理的做法是 相等几率,强制 两个标签的成功率相同。
机会平等的另一个缺点是,它会评估公平性
比较不同受众特征群体的错误率,
并不总是可行的。例如,如果登记模型的数据集
没有 demographic_group 功能,则无法
细分出合格的多数选民和少数族裔候选人的接受率
并比较它们,看看是否满足了机会平等。
在下一节中,我们将了解另一个公平性指标, 公平性,可在受众特征数据 所有样本都存在。
练习:检查您的理解情况
模型的预测有可能同时满足受众特征 机会平等和平等
例如,假设有一个二元分类器(其首选标签 是正类别)对 100 个样本进行评估, 如以下混淆矩阵所示, 受众特征群体(大多数人和少数群体):
| 多数派 | 少数群体 | |||
|---|---|---|---|---|
| 预测为正例 | 预测为负例 | 预测为正例 | 预测为负例 | |
| 实际正例 | 6 | 12 | 3 | 6 |
| 实际负例 | 10 | 36 | 6 | 21 |
|
\(\text{Positive Rate} = \frac{6+10}{6+10+12+36} = \frac{16}{64} = \text{25%}\) \(\text{True Positive Rate} = \frac{6}{6+12} = \frac{6}{18} = \text{33%}\) |
\(\text{Positive Rate} = \frac{3+6}{3+6+6+21} = \frac{9}{36} = \text{25%}\) \(\text{True Positive Rate} = \frac{3}{3+6} = \frac{3}{9} = \text{33%}\) |
|||
多数群体和少数群体的预测率均为正数 达到 25%,满足受众特征一致性要求,并且具有真正例率 (在 正确分类的概率为 33%,这可满足机会均等的需要。
