공정성: 기회의 균등

이전 섹션에서는 두 집단의 전체 수락률을 비교하여 확인할 수 있습니다.

또는 조건을 충족하는 조건의 수락률을 과반수 집단과 소수 집단의 후보자입니다. 수락률이 두 그룹의 적격한 학생이 동일하다면 모델이 기회의 균등: 선호하는 라벨('입학 자격')이 있는 학생의 경우 속한 인구통계 그룹과 관계없이 입학 확률 있습니다.

이전 섹션의 후보 풀을 다시 살펴보겠습니다.

	다수 집단	소수 집단
자격 있음	35	15
Unqualified(자격 없음)	45	5

입학 모델이 대다수 그룹에서 14명의 후보자를 승인한다고 가정하겠습니다. 소수 집단에서 6명의 후보가 선정되었습니다. 모델의 결정은 기회의 균등, 즉 적격 대다수의 수용율이 적합한 소수 집단 후보는 40%입니다

그림 4. 거부 및 수락된 후보 분류(모두 포함) 음영 처리된 대다수와 소수 집단의 유능한 학생 표시됩니다. 자격을 갖춘 과반수 집단 학생 35명 중 14명은 동의합니다. 자격을 갖춘 소수 집단 학생 15명 중 6명은 동의합니다. 따라서 두 그룹 모두 수락률은 40% 입니다. 학생으로 꼽을 수 있습니다

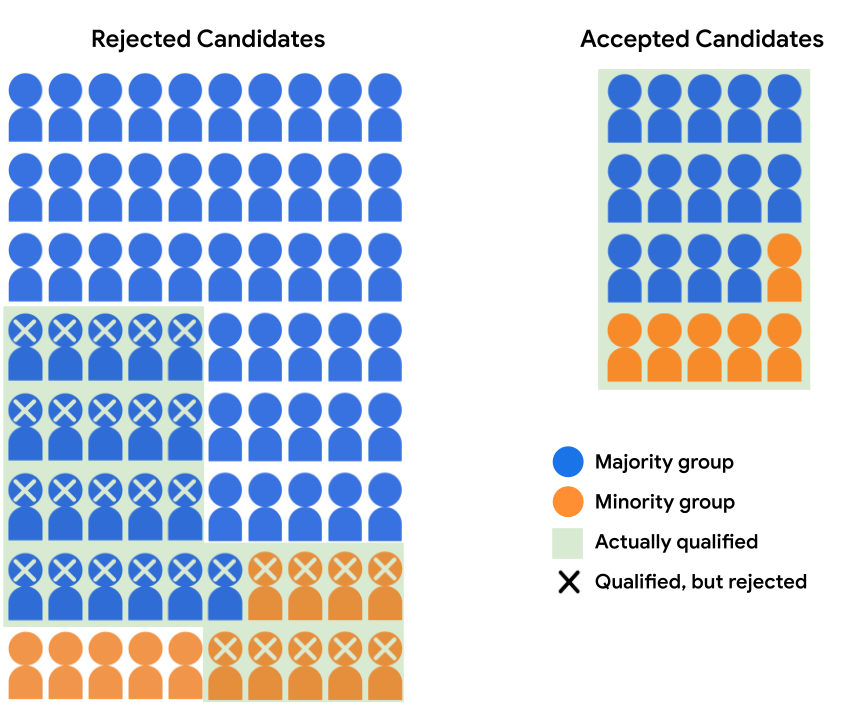
다음 표에는 거부 및 수락된 테스트를 뒷받침하는 수치를 수치로 제시하고 있습니다. 가능성이 있습니다.

	다수 집단		소수 집단
	수락됨	거부됨	수락됨	거부됨
자격 있음	14	21	6	9
Unqualified(자격 없음)	0	45	0	5

장단점

기회의 균등의 주요 이점은 모델의 예측이 인구통계 그룹에 따라 양성 예측 대비 음성 예측의 비율 모델이 선호 라벨을 예측하는 데 똑같이 성공할 경우 ('입학 자격')을 받게 됩니다.

그림 4의 모델 예측은 인구통계 동등성을 충족하지 않습니다. 과반수 그룹의 학생으로 채택될 가능성은 17.5% 이며 소수 집단의 학생 중 입학 가능성이 30% 인 경우 하지만 자격 요건을 충족하는 학생의 경우 합격 확률은 40% 입니다. 이론상 타당한 결과를 보여주는 것으로 특정 모델 사용 사례를 살펴보겠습니다

기회의 균등의 한 가지 단점은 모든 AI가 명확한 선호 라벨이 있는 경우입니다. 마찬가지로 모델이 포지티브 클래스('입학 자격')를 모두 예측한다는 것을 네거티브 클래스('입학 자격 미충족')로 분류하면 대신 측정항목을 사용하여 균등화된 승산은 성공률이 같아야 합니다.

기회의 균등의 또 다른 단점은 공정성을 평가한다는 것입니다. 인구통계 그룹에 대해 집계된 오류율을 비교하여 항상 실행 가능하지는 않습니다 예를 들어 입장권 모델의 데이터 세트가 demographic_group 기능이 없으면 다음 작업을 할 수 없습니다. 적격 대다수 및 소수 후보의 수락률 분석 이를 비교하여 기회의 균등이 충족되는지 확인합니다.

다음 섹션에서는 또 다른 공정성 측정항목인 반사실적인 시나리오에 적용할 수 있는 공정성입니다. 항상 존재합니다

연습문제: 학습 내용 점검하기

참 또는 거짓: 이진 분류 모델은 불가능함 동일한 환경에서의 인구통계 동등성과 기회의 균등을 모두 사용할 수 있습니다

참

모델의 예측이 두 인구통계를 모두 만족시킬 수 있습니다. 기회의 평등과 기회의 균등입니다. 데이터 애널리스트가 사용할 수 있는 두 측정항목이 모두 충족되는 경우를 보고 나머지 측정항목을 아래의 답변을 선택하여 설명을 확인하세요.

거짓

모델의 예측이 두 인구통계를 모두 만족시킬 수 있습니다. 기회의 평등과 기회의 균등입니다.

예를 들어 '주목할 만한 분류 기준'이라는 포지티브 클래스임)을 평가한 결과 는 다음과 같은 혼동 행렬에서 볼 수 있으며, 인구통계 그룹 (대다수 및 소수):

	다수결		소수 집단
	양성 예측	음성 예측	양성 예측	음성 예측
실제 양성	6	12	3	6
실제 음성	10	36	6	21
	\(\text{Positive Rate} = \frac{6+10}{6+10+12+36} = \frac{16}{64} = \text{25%}\) \(\text{True Positive Rate} = \frac{6}{6+12} = \frac{6}{18} = \text{33%}\)		\(\text{Positive Rate} = \frac{3+6}{3+6+6+21} = \frac{9}{36} = \text{25%}\) \(\text{True Positive Rate} = \frac{3}{3+6} = \frac{3}{9} = \text{33%}\)

대다수와 소수 집단 모두 양성 예측률을 보입니다. 25%, 인구통계 동등성 충족, 참양성률 (선호하는 라벨이 있는 예시의 비율 33%로 평가하여 기회의 평등을 충족합니다.

핵심 용어:

• 편향성 (윤리/공정성)
• 기회의 평등
• 균등화된 확률