Sobreajuste: Se refiere a la creación de un modelo que coincida (memorice) con el conjunto de entrenamiento de tal manera que no pueda realizar predicciones correctas con datos nuevos. Un modelo sobreajustado es análogo a un invento que funciona bien en el laboratorio, pero que no tiene valor en el mundo real.
En la Figura 11, imagina que cada forma geométrica representa la posición de un árbol en un bosque cuadrado. Los diamantes azules marcan las ubicaciones de los árboles sanos, mientras que los círculos naranjas marcan las ubicaciones de los árboles enfermos.

Dibuja mentalmente cualquier forma (líneas, curvas, óvalos, etc.) para separar los árboles sanos de los enfermos. Luego, expande la siguiente línea para examinar una posible separación.
Las formas complejas que se muestran en la Figura 12 categorizaron correctamente todos los árboles, excepto dos. Si pensamos en las formas como un modelo, este es un modelo fantástico.
¿O no? Un modelo realmente excelente clasifica correctamente los ejemplos nuevos. En la Figura 13, se muestra lo que sucede cuando ese mismo modelo realiza predicciones sobre ejemplos nuevos del conjunto de prueba:

Por lo tanto, el modelo complejo que se muestra en la Figura 12 hizo un gran trabajo en el conjunto de entrenamiento, pero un trabajo bastante malo en el conjunto de prueba. Este es un caso clásico de un modelo que se sobreajusta a los datos del conjunto de entrenamiento.
Ajuste, sobreajuste y subajuste
Un modelo debe realizar buenas predicciones sobre datos nuevos. Es decir, tu objetivo es crear un modelo que “se ajuste” a los datos nuevos.
Como viste, un modelo con sobreajuste realiza predicciones excelentes en el conjunto de entrenamiento, pero predicciones deficientes en los datos nuevos. Un modelo con subajuste ni siquiera realiza buenas predicciones en los datos de entrenamiento. Si un modelo sobreajustado es como un producto que funciona bien en el laboratorio, pero mal en el mundo real, un modelo subajustado es como un producto que ni siquiera funciona bien en el laboratorio.

La generalización es lo opuesto al sobreajuste. Es decir, un modelo que generaliza bien realiza buenas predicciones sobre datos nuevos. Tu objetivo es crear un modelo que generalice los datos nuevos de forma correcta.
Cómo detectar el sobreajuste
Las siguientes curvas te ayudan a detectar el sobreajuste:
- curvas de pérdida
- curvas de generalización
Una curva de pérdida grafica la pérdida de un modelo en función de la cantidad de iteraciones de entrenamiento. Un gráfico que muestra dos o más curvas de pérdida se denomina curva de generalización. En la siguiente curva de generalización, se muestran dos curvas de pérdida:
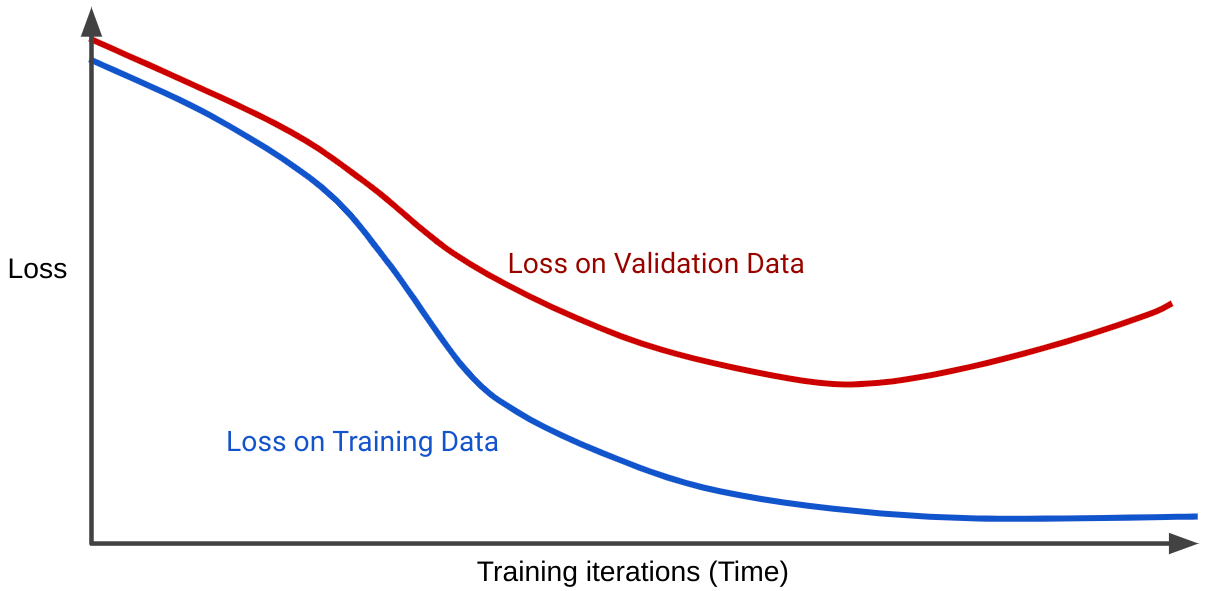
Observa que las dos curvas de pérdida se comportan de manera similar al principio y, luego, divergen. Es decir, después de una cierta cantidad de iteraciones, la pérdida disminuye o se mantiene constante (converge) para el conjunto de entrenamiento, pero aumenta para el conjunto de validación. Esto sugiere un sobreajuste.
En cambio, una curva de generalización para un modelo bien ajustado muestra dos curvas de pérdida que tienen formas similares.
¿Qué causa el sobreajuste?
En términos generales, el sobreajuste se debe a uno o ambos de los siguientes problemas:
- El conjunto de entrenamiento no representa de manera adecuada los datos de la vida real (o el conjunto de validación o el conjunto de prueba).
- El modelo es demasiado complejo.
Condiciones de generalización
Un modelo se entrena en un conjunto de entrenamiento, pero la prueba real de su valor es qué tan bien hace predicciones sobre ejemplos nuevos, en particular, sobre datos del mundo real. Mientras desarrollas un modelo, tu conjunto de prueba sirve como proxy para los datos del mundo real. El entrenamiento de un modelo que generalice bien implica las siguientes condiciones del conjunto de datos:
- Los ejemplos deben ser independientes y estar idénticamente distribuidos, que es una forma elegante de decir que tus ejemplos no pueden influir entre sí.
- El conjunto de datos es estacionario, lo que significa que no cambia de forma significativa con el tiempo.
- Las particiones del conjunto de datos tienen la misma distribución. Es decir, los ejemplos del conjunto de entrenamiento son estadísticamente similares a los ejemplos del conjunto de validación, el conjunto de prueba y los datos del mundo real.
Explora las condiciones anteriores a través de los siguientes ejercicios.
Ejercicios: Comprueba tu comprensión

Ejercicio de desafío
Estás creando un modelo que predice la fecha ideal para que los pasajeros compren un boleto de tren para una ruta en particular. Por ejemplo, el modelo podría recomendar que los usuarios compren su boleto el 8 de julio para un tren que sale el 23 de julio. La empresa de trenes actualiza los precios por hora en función de una variedad de factores, pero principalmente en función de la cantidad actual de asientos disponibles. Es decir:
- Si hay muchos asientos disponibles, los precios de los boletos suelen ser bajos.
- Si hay muy pocos asientos disponibles, los precios de los boletos suelen ser altos.
Respuesta: El modelo del mundo real tiene problemas con un bucle de retroalimentación.
Por ejemplo, supongamos que el modelo recomienda que los usuarios compren boletos el 8 de julio. Algunos pasajeros que usan la recomendación del modelo compran sus boletos a las 8:30 a.m. del 8 de julio. A las 9:00, la empresa de trenes sube los precios porque ahora hay menos asientos disponibles. Los pasajeros que usan la recomendación del modelo alteraron los precios. Por la tarde, los precios de las entradas pueden ser mucho más altos que por la mañana.

