Gradient descent היא טכניקה מתמטית שמוצאת באופן איטרטיבי את המשקלים וההטיה שמפיקים את המודל עם ההפסד הנמוך ביותר. האלגוריתם של ירידת גרדיאנט מוצא את המשקל וההטיה הטובים ביותר על ידי חזרה על התהליך הבא למספר איטרציות שהמשתמש מגדיר.
המודל מתחיל להתאמן עם משקלים והטיות אקראיים שקרובים לאפס, ואז חוזר על השלבים הבאים:
חישוב ההפסד עם המשקל וההטיה הנוכחיים.
קובעים את הכיוון להזזת המשקלים וההטיה שמפחיתים את השגיאה.
מזיזים את ערכי המשקל וההטיה במידה קטנה בכיוון שמקטין את השגיאה.
חוזרים לשלב הראשון וחוזרים על התהליך עד שהמודל לא יכול להקטין יותר את השגיאה.
הדיאגרמה הבאה מתארת את השלבים האיטרטיביים של ירידת הגרדיאנט, שמתבצעת כדי למצוא את המשקלים וההטיה שמפיקים את המודל עם ההפסד הנמוך ביותר.
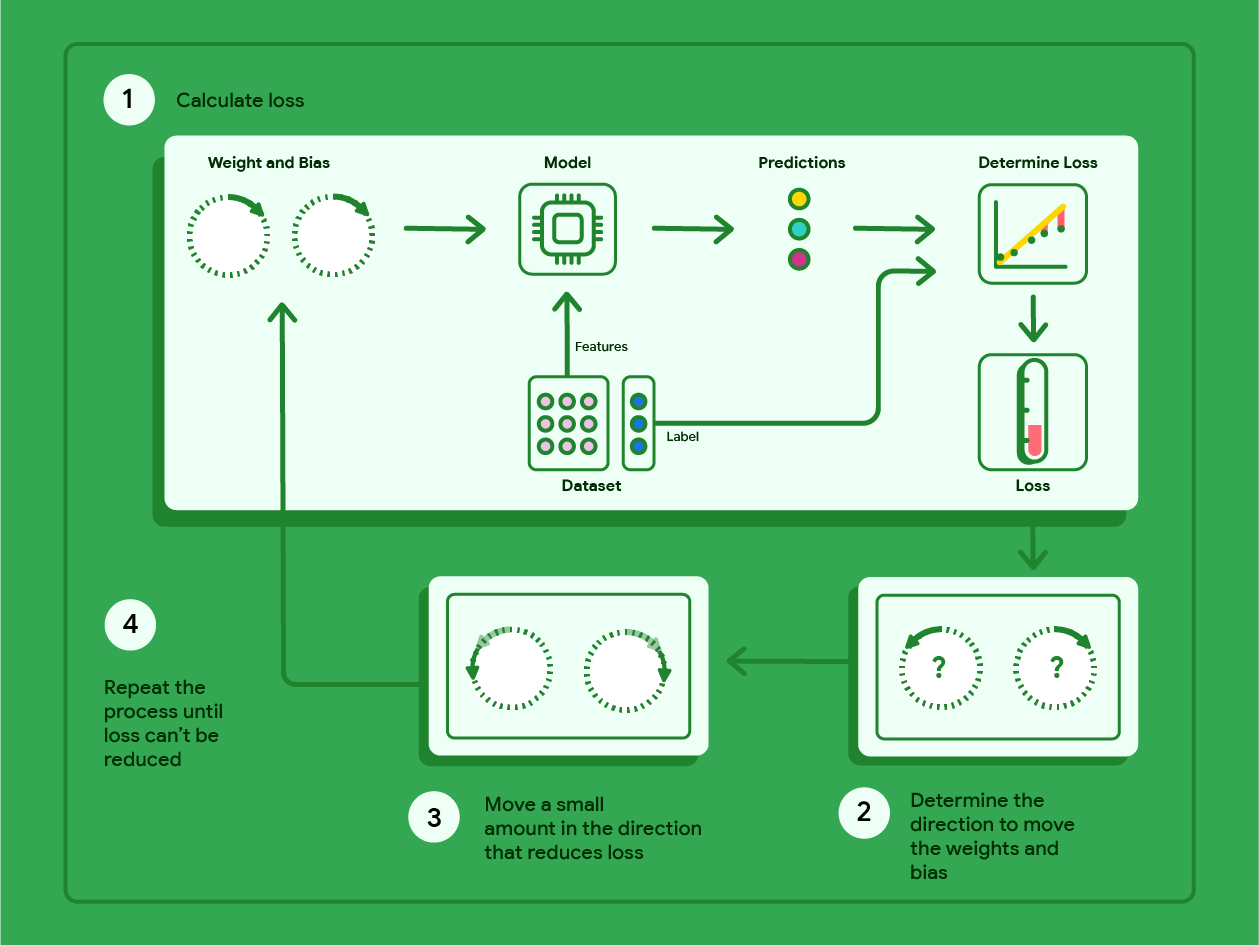
איור 11. Gradient descent (ירידת גרדיאנט) הוא תהליך איטרטיבי שמוצא את המשקלים וההטיה שמפיקים את המודל עם ההפסד הכי נמוך.
כדי לקבל מידע נוסף על המתמטיקה שמאחורי שיטת הגרדיאנט, לוחצים על סמל הפלוס.
ברמה הקונקרטית, אפשר לעבור על השלבים של ירידת הגרדיאנט באמצעות מערך נתונים קטן עם שבע דוגמאות של משקל מכונית בליברות ודירוג המיילים שלה לגלון:
| פאונד באלפים (תכונה) | מיילים לגלון (תווית) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- האימון של המודל מתחיל בהגדרת המשקל וההטיה לאפס:
- מחשבים את הפסד ה-MSE באמצעות הפרמטרים הנוכחיים של המודל:
- מחשבים את השיפוע של הטנגנס לפונקציית ההפסד בכל משקל והטיה:
- כדי לקבל את המשקל וההטיה הבאים, מבצעים תזוזה קטנה בכיוון של השיפוע השלילי. לבינתיים, נגדיר באופן שרירותי את ה"סכום הקטן" כ-0.01:
כדי לקבל מידע על חישוב השיפוע, לוחצים על סמל הפלוס.
כדי לקבל את השיפוע של הקווים המשיקים למשקל ול-bias, גוזרים את פונקציית ההפסד ביחס למשקל ול-bias, ואז פותרים את המשוואות.
המשוואה ליצירת תחזית תהיה:
$ f_{w,b}(x) = (w*x)+b $.
הערך בפועל יופיע כך: $ y $.
נחשב את MSE באמצעות הנוסחה הבאה:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
כאשר $i$ מייצג את דוגמת האימון ה-$ith$ ו-$M$ מייצג את מספר הדוגמאות.
הנגזרת של פונקציית ההפסד ביחס למשקל נכתבת כך:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
והערך שלה הוא:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
קודם כל מחשבים את הסכום של כל ערך חזוי פחות הערך בפועל ואז מכפילים אותו בערך התכונה כפול שתיים. לאחר מכן מחלקים את הסכום במספר הדוגמאות. התוצאה היא השיפוע של קו המשיק לערך של המשקל.
אם נפתור את המשוואה הזו עם משקל והטיה ששווים לאפס, נקבל את הערך -119.7 עבור השיפוע של הקו.
נגזרת של הטיה
הנגזרת של פונקציית ההפסד ביחס להטיה נכתבת כך:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
והערך שלה הוא:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
קודם מחשבים את הסכום של כל ערך חזוי פחות הערך בפועל ואז מכפילים אותו בשניים. לאחר מכן מחלקים את הסכום במספר הדוגמאות. התוצאה היא שיפוע הקו המשיק לערך של הטיה.
אם נפתור את המשוואה הזו עם משקל והטיה ששווים לאפס, נקבל את הערך -34.3 עבור השיפוע של הקו.
משתמשים במשקל החדש ובטיה כדי לחשב את ההפסד ולחזור על הפעולה. אחרי שש חזרות של התהליך, נקבל את המשקלים, ההטיות וההפסדים הבאים:
| איטרציה | משקל | הטיה | הפסד (MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
אפשר לראות שההפסד קטן יותר עם כל עדכון של המשקל וההטיה. בדוגמה הזו, הפסקנו אחרי שש חזרות. בפועל, המודל עובר אימון עד שהוא מתכנס. כשמודל מתכנס, איטרציות נוספות לא מפחיתות את השגיאה יותר, כי שיטת הגרדיאנט מצאה את המשקלים וההטיה שממזערים את השגיאה כמעט לחלוטין.
אם המודל ממשיך להתאמן אחרי ההתכנסות, ערך הפונקציה מתחיל לנוע בתנודות קלות כי המודל מעדכן כל הזמן את הפרמטרים סביב הערכים הנמוכים ביותר שלהם. לכן קשה לאמת שהמודל באמת התכנס. כדי לוודא שהמודל הגיע למצב של התכנסות, צריך להמשיך באימון עד שההפסד יתייצב.
התכנסות המודל ועקומות ההפסד
במהלך אימון מודל, בדרך כלל בודקים עקומת הפסד כדי לקבוע אם המודל התכנס. עקומת ההפסד מראה איך ההפסד משתנה במהלך אימון המודל. התרשים הבא מציג עקומת הפסד אופיינית. ההפסד מוצג בציר ה-Y והאיטרציות מוצגות בציר ה-X:
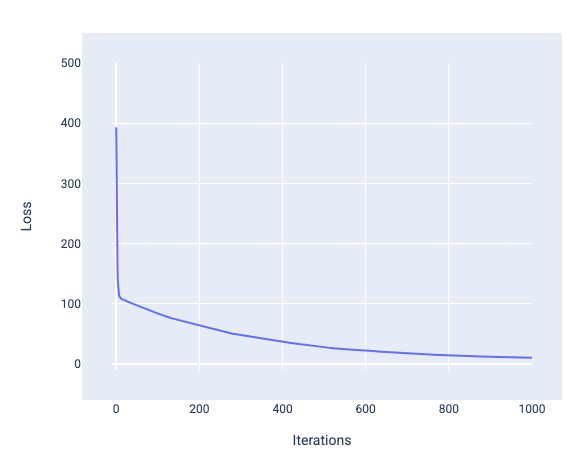
איור 12. עקומת אובדן שמראה שהמודל מתכנס סביב סימן האיטרציה ה-1,000.
אפשר לראות שההפסד יורד באופן משמעותי במהלך כמה האיטרציות הראשונות, ואז יורד בהדרגה עד שהוא מתייצב סביב האיטרציה ה-1,000. אחרי 1,000 איטרציות, אפשר להיות בטוחים במידה רבה שהמודל הגיע למצב של התכנסות.
באיורים הבאים אנחנו מציגים את המודל בשלוש נקודות במהלך תהליך האימון: בהתחלה, באמצע ובסוף. הדמיה של מצב המודל בתמונות מצב במהלך תהליך האימון מחזקת את הקשר בין עדכון המשקלים וההטיה, צמצום ההפסד והתכנסות המודל.
באיורים, אנחנו משתמשים במשקלים ובערכי ההטיה שהתקבלו באיטרציה מסוימת כדי לייצג את המודל. בגרף עם נקודות הנתונים ותמונת המצב של המודל, קווים כחולים של הפסדים מהמודל לנקודות הנתונים מראים את כמות ההפסדים. ככל שהשורות ארוכות יותר, כך האובדן גדול יותר.
באיור הבא אפשר לראות שסביב האיטרציה השנייה, המודל לא יצליח לבצע חיזויים בגלל כמות ההפסד הגבוהה.
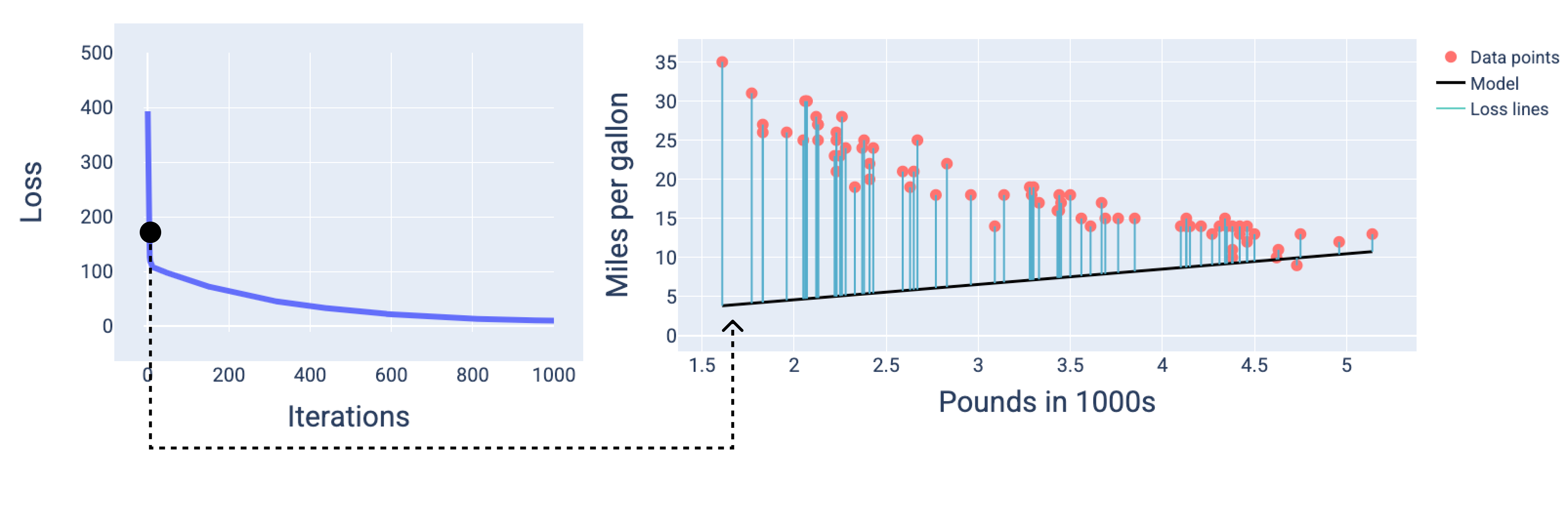
איור 13. עקומת ההפסד ותמונת מצב של המודל בתחילת תהליך האימון.
באיטרציה ה-400 בערך, אפשר לראות שהאלגוריתם של ירידת הגרדיאנט מצא את המשקל וההטיה שיוצרים מודל טוב יותר.
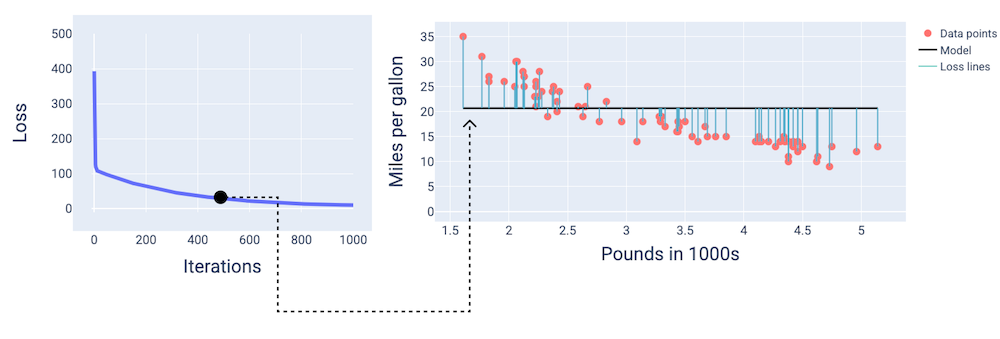
איור 14. עקומת הפסד ותמונת מצב של המודל באמצע האימון.
ובערך באיטרציה ה-1,000, אפשר לראות שהמודל הגיע למצב של התכנסות, כלומר הוא מייצר מודל עם הפסד נמוך ככל האפשר.
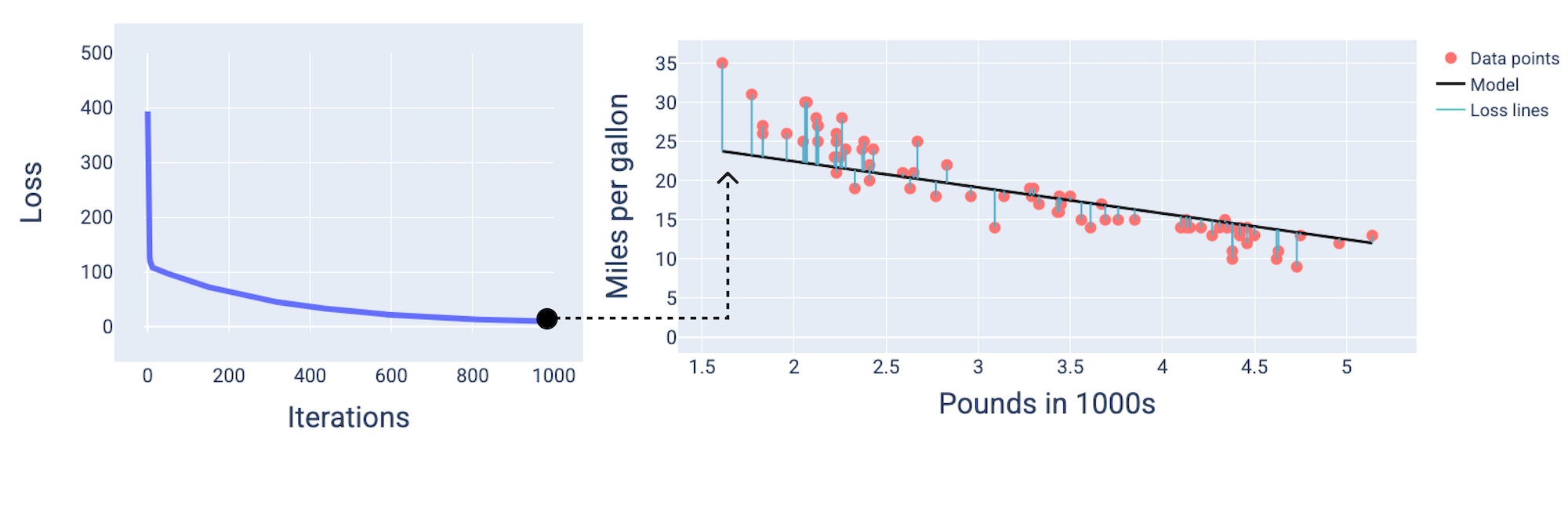
איור 15. עקומת ההפסד ותמונת מצב של המודל לקראת סוף תהליך האימון.
תרגיל: בדיקת ההבנה
התכנסות ופונקציות קמורות
פונקציות ההפסד של מודלים לינאריים תמיד יוצרות משטח קמור. כתוצאה מהמאפיין הזה, כשמודל רגרסיה לינארית מתכנס, אנחנו יודעים שהמודל מצא את המשקלים וההטיה שמניבים את ההפסד הנמוך ביותר.
אם נשרטט את משטח ההפסד של מודל עם תכונה אחת, נוכל לראות את הצורה הקמורה שלו. התרשים הבא מציג את פני השטח של אובדן נתונים עבור מערך נתונים היפותטי של מיילים לגלון. המשקל מוצג בציר ה-X, ההטיה מוצגת בציר ה-Y וההפסד מוצג בציר ה-Z:
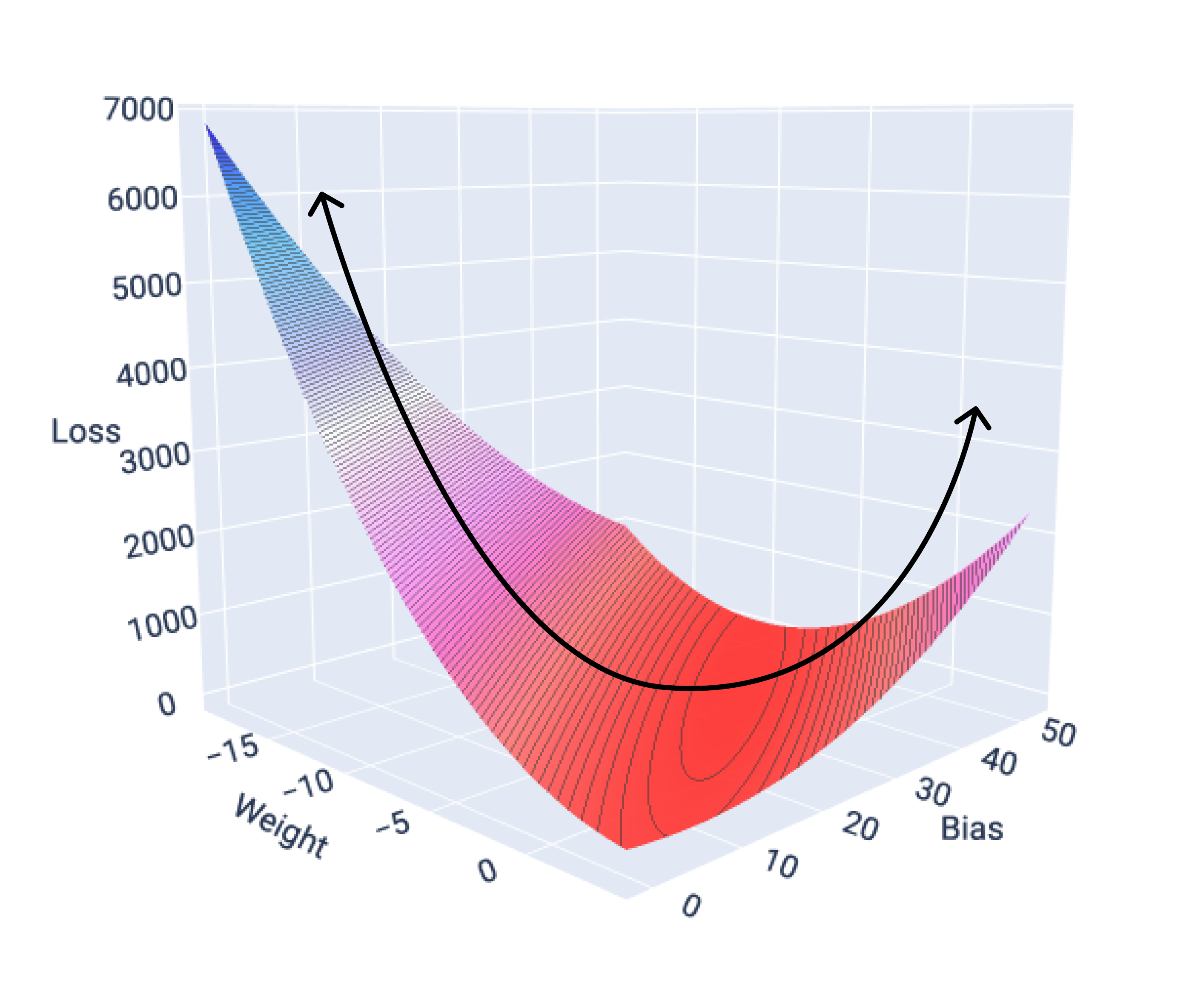
איור 16. משטח הפסד שמציג את הצורה הקמורה שלו.
בדוגמה הזו, משקל של -5.44 והטיה של 35.94 מניבים את ההפסד הנמוך ביותר של 5.54:
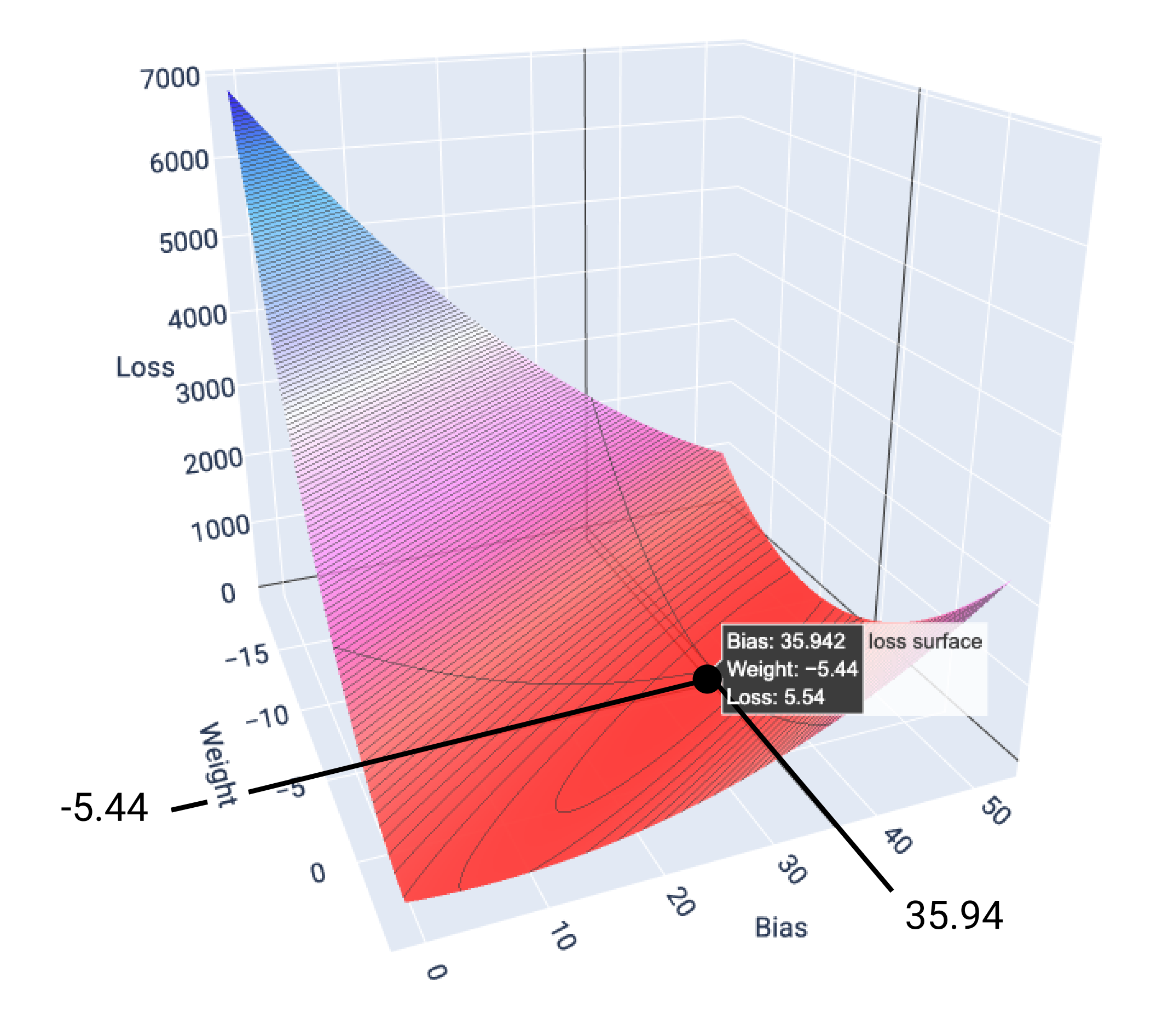
איור 17. משטח הפסד שמציג את ערכי המשקל וההטיה שמניבים את ההפסד הנמוך ביותר.
מודל ליניארי מגיע למצב של התכנסות כשהוא מוצא את ההפסד המינימלי. לכן, איטרציות נוספות רק גורמות לירידה בשיפוע להזיז את ערכי המשקל וההטיה בסכומים קטנים מאוד סביב המינימום. אם היינו משרטטים גרף של המשקלים ונקודות ההטיה במהלך ירידת הגרדיאנט, הנקודות היו נראות כמו כדור שמתגלגל במורד גבעה, ובסופו של דבר נעצר בנקודה שבה אין יותר שיפוע כלפי מטה.
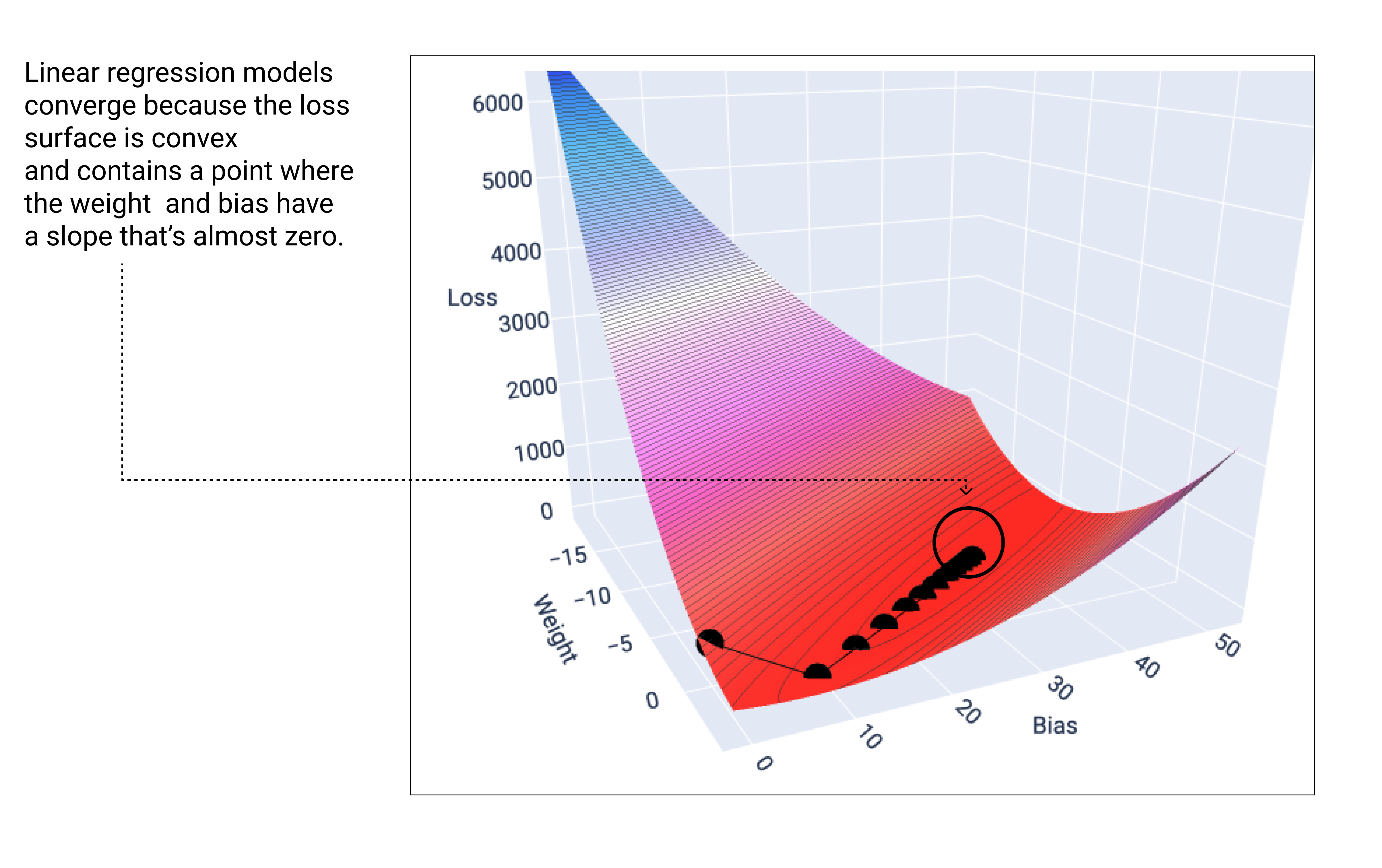
איור 18. גרף הפסדים שמציג נקודות של ירידה הדרגתית שעוצרות בנקודה הנמוכה ביותר בגרף.
שימו לב שנקודות האובדן השחורות יוצרות את הצורה המדויקת של עקומת האובדן: ירידה חדה לפני שהיא מתמתנת בהדרגה עד שהיא מגיעה לנקודה הנמוכה ביותר במשטח האובדן.
חשוב לציין שהמודל כמעט אף פעם לא מוצא את המינימום המדויק של כל משקל והטיה, אלא מוצא ערך שקרוב מאוד למינימום. חשוב גם לציין שהערך המינימלי של המשקלים וההטיה לא מייצג הפסד אפס, אלא רק ערך שמניב את ההפסד הנמוך ביותר עבור הפרמטר הזה.
בעזרת ערכי המשקל וההטיה שמניבים את ההפסד הנמוך ביותר – במקרה הזה משקל של -5.44 והטיה של 35.94 – אפשר לשרטט את המודל כדי לראות עד כמה הוא מתאים לנתונים:
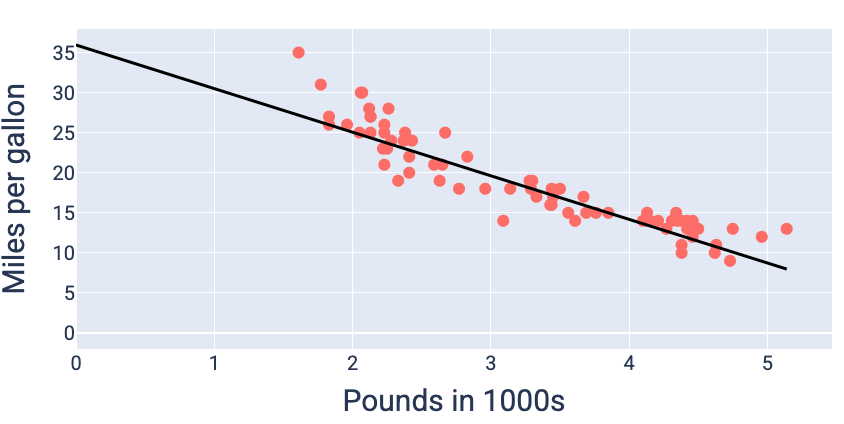
איור 19. מודל שמוצג בתרשים באמצעות ערכי המשקל וההטיה שמניבים את ההפסד הנמוך ביותר.
זה יהיה המודל הטוב ביותר עבור מערך הנתונים הזה, כי אין ערכים אחרים של משקל והטיה שמניבים מודל עם הפסד נמוך יותר.
