היפרפרמטרים הם משתנים ששולטים בהיבטים שונים של האימון. שלושה היפר-פרמטרים נפוצים הם:
לעומת זאת, פרמטרים הם המשתנים, כמו המשקלים וההטיה, שהם חלק מהמודל עצמו. במילים אחרות, היפר-פרמטרים הם ערכים שאתם שולטים בהם, ופרמטרים הם ערכים שהמודל מחשב במהלך האימון.
קצב למידה
שיעור הלמידה הוא מספר נקודה צפה שאתם מגדירים, והוא משפיע על מהירות ההתכנסות של המודל. אם קצב הלמידה נמוך מדי, יכול לעבור הרבה זמן עד שהמודל יתכנס. עם זאת, אם קצב הלמידה גבוה מדי, המודל אף פעם לא מתכנס, אלא נע בין המשקלים וההטיות שממזערים את ההפסד. המטרה היא לבחור קצב למידה שלא יהיה גבוה מדי ולא נמוך מדי, כדי שהמודל יתכנס במהירות.
שיעור הלמידה קובע את גודל השינויים שצריך לבצע במשקלים וב-bias במהלך כל שלב בתהליך של ירידת הגרדיאנט. המודל מכפיל את הגרדיאנט בקצב הלמידה כדי לקבוע את הפרמטרים של המודל (משקל וערכי הטיה) לאיטרציה הבאה. בשלב השלישי של gradient descent, ה'כמות הקטנה' שצריך להזיז בכיוון של השיפוע השלילי מתייחסת לשיעור הלמידה.
ההבדל בין הפרמטרים של המודל הישן לבין הפרמטרים של המודל החדש הוא פרופורציונלי לשיפוע של פונקציית ההפסד. לדוגמה, אם השיפוע גדול, המודל מבצע צעד גדול. אם הוא קטן, הוא יזוז צעד קטן. לדוגמה, אם גודל הגרדיאנט הוא 2.5 וקצב הלמידה הוא 0.01, המודל ישנה את הפרמטר ב-0.025.
שיעור הלמידה האידיאלי עוזר למודל להתכנס בתוך מספר סביר של איטרציות. בתרשים 20, עקומת ההפסד מראה שיפור משמעותי במודל במהלך 20 האיטרציות הראשונות לפני שהמודל מתחיל להתכנס:
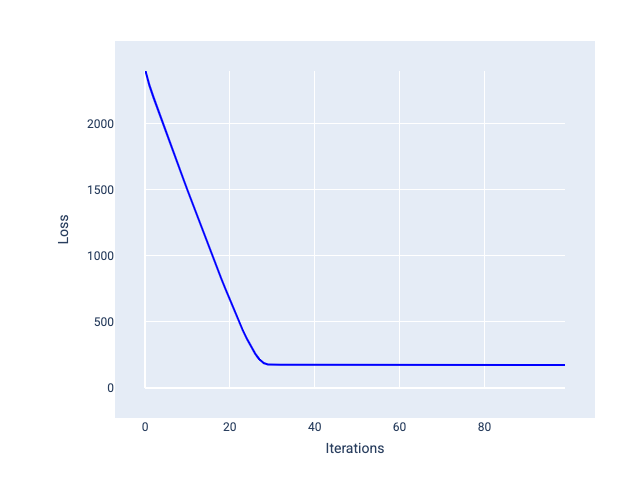
איור 20. תרשים של אובדן שמציג מודל שאומן עם קצב למידה שמתכנס במהירות.
לעומת זאת, אם קצב הלמידה קטן מדי, יכול להיות שיידרשו יותר מדי איטרציות כדי להגיע להתכנסות. באיור 21, עקומת ההפסד מראה שהמודל מבצע שיפורים קלים בלבד אחרי כל איטרציה:
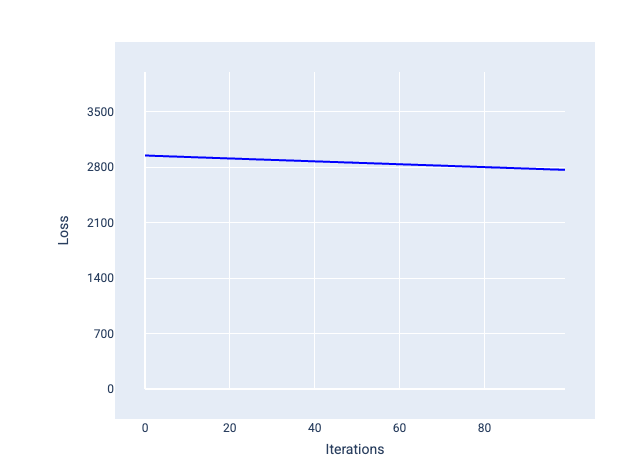
איור 21. תרשים הפסדים שבו מוצג מודל שאומן עם קצב למידה נמוך.
שיעור למידה גדול מדי אף פעם לא מתכנס כי כל איטרציה גורמת להפסד לנוע בצורה לא צפויה או לעלות באופן מתמשך. באיור 22, עקומת ההפסד מראה שההפסד של המודל יורד ואז עולה אחרי כל איטרציה, ובאיור 23 ההפסד עולה באיטרציות מאוחרות יותר:
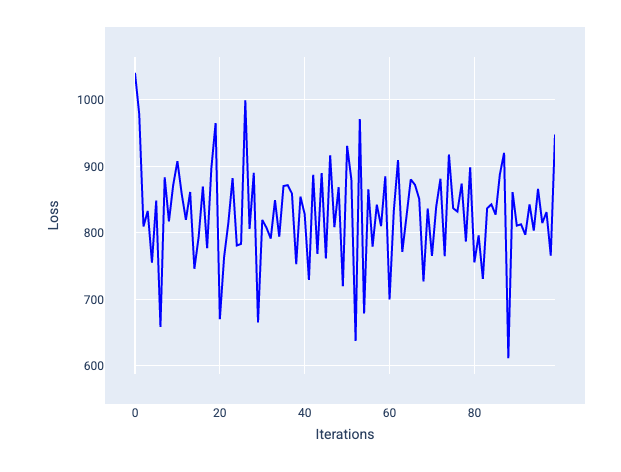
איור 22. תרשים הפסדים שבו מוצג מודל שאומן עם קצב למידה גדול מדי, שבו עקומת ההפסדים משתנה באופן קיצוני, ועולה ויורדת ככל שמספר האיטרציות גדל.
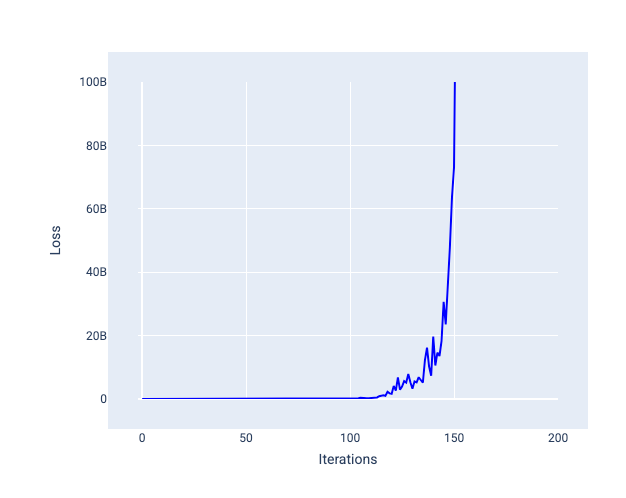
איור 23. תרשים הפסדים שמציג מודל שאומן עם קצב למידה גדול מדי, שבו עקומת ההפסדים עולה באופן משמעותי באיטרציות מאוחרות יותר.
תרגיל: בדיקת ההבנה
גודל אצווה
גודל קבוצת הפריטים הוא היפרפרמטר שמתייחס למספר הדוגמאות שהמודל מעבד לפני שהוא מעדכן את המשקלים וההטיה שלו. יכול להיות שתחשבו שהמודל צריך לחשב את ההפסד עבור כל דוגמה במערך הנתונים לפני עדכון המשקלים וההטיה. עם זאת, אם מערך הנתונים מכיל מאות אלפים או אפילו מיליוני דוגמאות, לא מעשי להשתמש באצווה מלאה.
שתי טכניקות נפוצות להשגת השיפוע הנכון בממוצע בלי לבדוק כל דוגמה במערך הנתונים לפני עדכון המשקלים וההטיה הן ירידת שיפוע סטוכסטית וירידת שיפוע סטוכסטית של אצווה קטנה:
ירידת גרדיאנט סטוכסטית (SGD): ירידת גרדיאנט סטוכסטית משתמשת רק בדוגמה אחת (גודל אצווה של אחד) לכל איטרציה. אם יש מספיק איטרציות, SGD פועל אבל הוא מאוד רועש. 'רעש' מתייחס לשינויים במהלך האימון שגורמים להפסד לגדול במקום לקטון במהלך איטרציה. המונח 'סטוכסטי' מציין שהדוגמה היחידה שמרכיבה כל אצווה נבחרת באופן אקראי.
בתמונה הבאה אפשר לראות שההפסד משתנה מעט כשהמודל מעדכן את המשקלים וההטיה שלו באמצעות SGD, מה שיכול להוביל לרעש בגרף ההפסד:
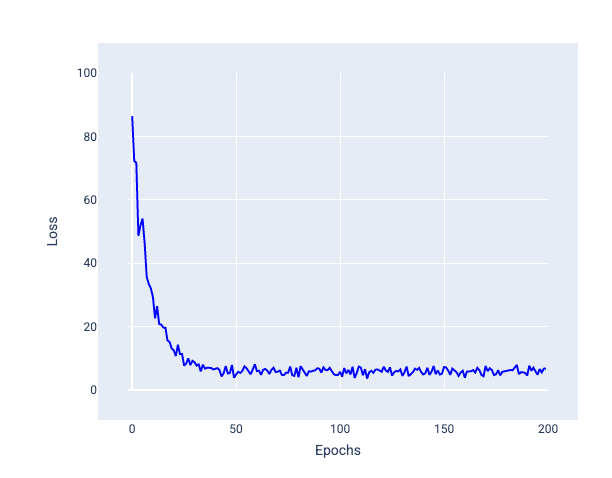
איור 24. מודל שאומן באמצעות ירידה סטוכסטית של הגרדיאנט (SGD) ומציג רעש בעקומת ההפסד.
שימו לב ששימוש בשיטת הגרדיאנט הסטוכסטי יכול ליצור רעשים לאורך כל עקומת ההפסד, ולא רק ליד נקודת ההתכנסות.
ירידת גרדיאנט סטוכסטית של קבוצת נתונים קטנה (mini-batch SGD): ירידת גרדיאנט סטוכסטית של קבוצת נתונים קטנה היא פשרה בין ירידת גרדיאנט סטוכסטית של קבוצת נתונים מלאה לבין ירידת גרדיאנט סטוכסטית. אם יש $ N $ נקודות נתונים, גודל האצווה יכול להיות כל מספר גדול מ-1 וקטן מ-$ N $. המודל בוחר את הדוגמאות שנכללות בכל אצווה באופן אקראי, מחשב את ממוצע השיפועים שלהן ואז מעדכן את המשקלים וההטיה פעם אחת בכל איטרציה.
מספר הדוגמאות בכל אצווה תלוי במערך הנתונים ובמשאבי המחשוב הזמינים. באופן כללי, גודלי קבוצות קטנים מתנהגים כמו SGD, וגודלי קבוצות גדולים מתנהגים כמו ירידת גרדיאנט של קבוצה מלאה.
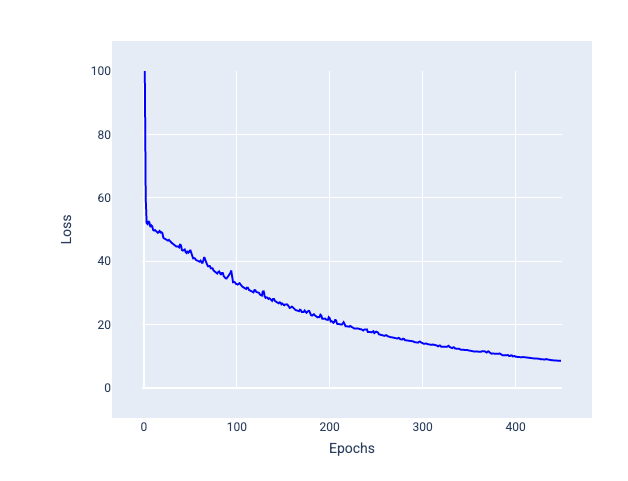
איור 25. מודל שאומן באמצעות SGD של מיני-batch.
כשמאמנים מודל, יכול להיות שתחשבו שרעש הוא מאפיין לא רצוי שצריך לסלק. עם זאת, רעשי רקע ברמה מסוימת יכולים להיות דבר טוב. במודולים הבאים תלמדו איך רעש יכול לעזור למודל להכליל טוב יותר ולמצוא את המשקלים וההטיות האופטימליים ברשת נוירונים.
Epochs
במהלך האימון, אפוק פירושו שהמודל עיבד כל דוגמה במערך האימון פעם אחת. לדוגמה, אם יש קבוצת אימון עם 1,000 דוגמאות וגודל של מיני-אצווה של 100 דוגמאות, יידרשו למודל 10 איטרציות כדי להשלים תקופה אחת.
בדרך כלל נדרשות הרבה תקופות אימון. כלומר, המערכת צריכה לעבד כל דוגמה במערך האימון מספר פעמים.
מספר האפוקים הוא היפרפרמטר שאתם מגדירים לפני שהמודל מתחיל באימון. במקרים רבים, תצטרכו לבצע ניסויים כדי להבין כמה תקופות נדרשות עד שהמודל יתכנס. באופן כללי, ככל שיש יותר תקופות אימון, המודל טוב יותר, אבל האימון גם לוקח יותר זמן.
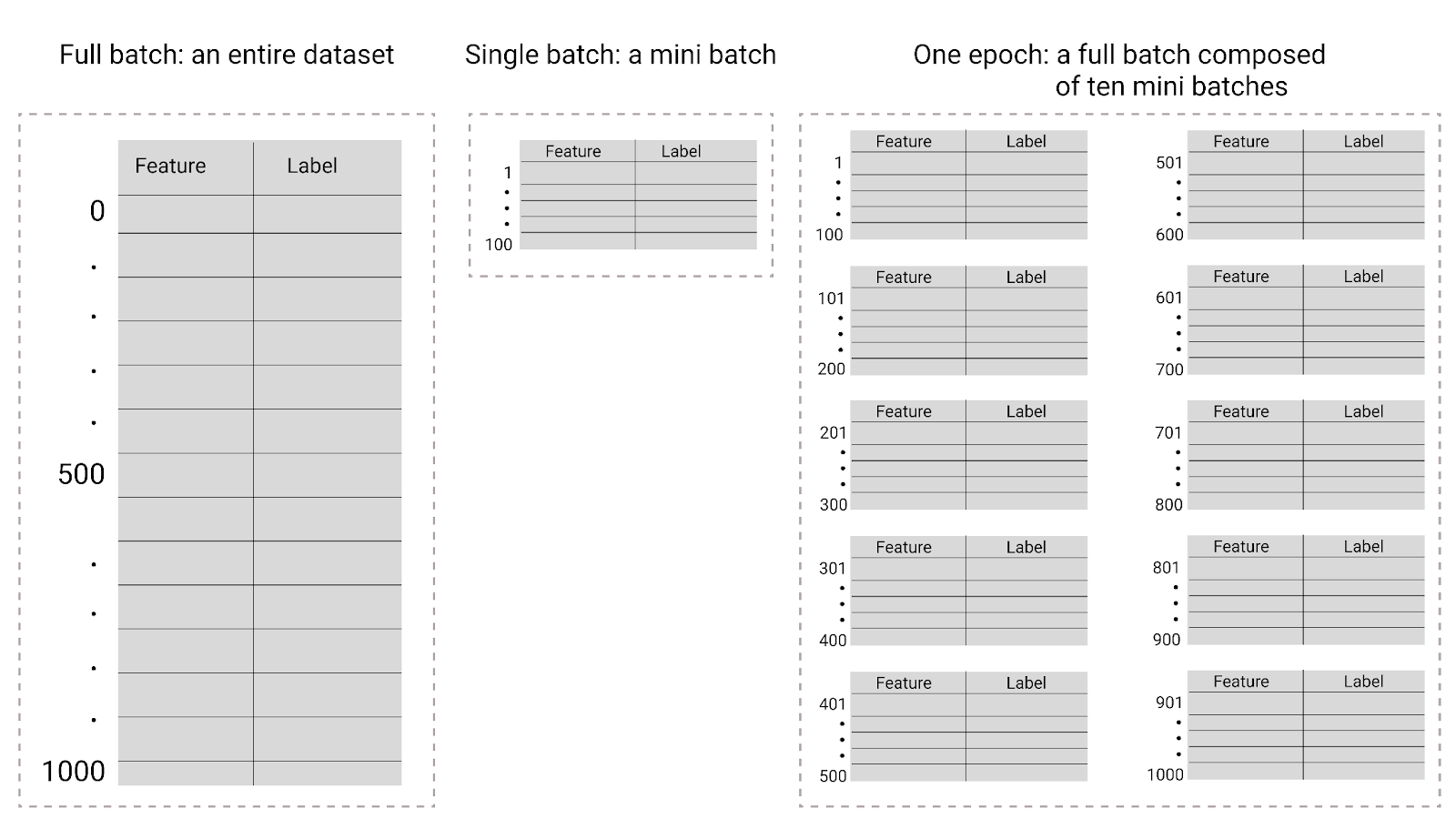
איור 26. אצווה מלאה לעומת אצווה קטנה.
בטבלה הבאה מוסבר הקשר בין גודל האצווה והתקופות לבין מספר הפעמים שבהן מודל מעדכן את הפרמטרים שלו.
| סוג המקבץ | מתי מתרחשים עדכונים של משקלים והטיות |
|---|---|
| Full batch | אחרי שהמודל בודק את כל הדוגמאות במערך הנתונים. לדוגמה, אם מערך נתונים מכיל 1,000 דוגמאות והמודל מתאמן במשך 20 תקופות, המודל מעדכן את המשקלים וההטיה 20 פעמים, פעם אחת בכל תקופה. |
| ירידה סטוכסטית של גרדיאנט | אחרי שהמודל בודק דוגמה אחת ממערך הנתונים. לדוגמה, אם מערך נתונים מכיל 1,000 דוגמאות והאימון נמשך 20 תקופות, המודל מעדכן את המשקלים וההטיה 20,000 פעמים. |
| ירידה סטוכסטית של גרדיאנטים במיני-אצווה | אחרי שהמודל בוחן את הדוגמאות בכל קבוצה. לדוגמה, אם מערך נתונים מכיל 1,000 דוגמאות, גודל האצווה הוא 100 והמודל מתאמן במשך 20 תקופות, המודל מעדכן את המשקלים וההטיה 200 פעמים. |