Потери — это числовая метрика, описывающая степень неточности предсказаний модели. Потери измеряют расстояние между предсказаниями модели и фактическими метками. Цель обучения модели — минимизировать потери, сведя их к минимально возможному значению.
На следующем изображении вы можете визуализировать потери в виде стрелок, проведенных от точек данных к модели. Стрелки показывают, насколько далеки прогнозы модели от фактических значений.
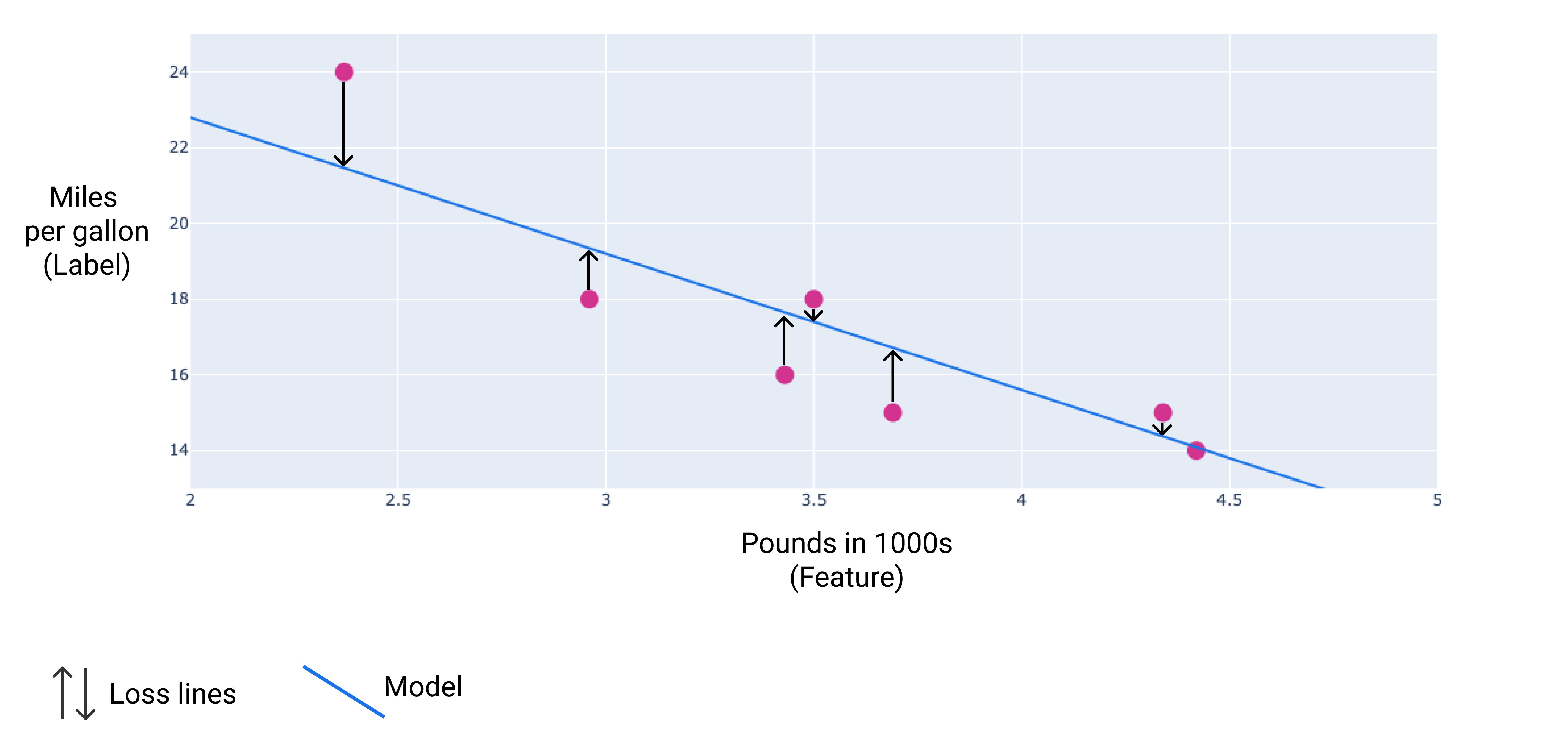
Рисунок 8. Убыток измеряется от фактического значения до прогнозируемого значения.
Расстояние потери
В статистике и машинном обучении потери измеряют разницу между предсказанными и фактическими значениями. Они фокусируются на расстоянии между значениями, а не на направлении. Например, если модель предсказывает 2, а фактическое значение равно 5, нас не волнует, что потери отрицательны (2 - 5 = -3). Вместо этого нас интересует расстояние между значениями, равное 3. Таким образом, все методы вычисления потерь удаляют знак.
Два наиболее распространенных метода удаления знака:
- Возьмите абсолютное значение разницы между фактическим значением и прогнозом.
- Возьмем квадрат разницы между фактическим значением и прогнозом.
Виды потерь
В линейной регрессии существует пять основных типов потерь, которые описаны в следующей таблице.
| Тип убытка | Определение | Уравнение |
|---|---|---|
| Потеря L 1 | Сумма абсолютных значений разницы между прогнозируемыми значениями и фактическими значениями. | $ ∑ | фактическое\ значение - прогнозируемое\ значение | $ |
| Средняя абсолютная ошибка (MAE) | Среднее значение потерь L1 для набора из N примеров. | $ \frac{1}{N} ∑ | фактическое\ значение - прогнозируемое\ значение | $ |
| потеря L 2 | Сумма квадратов разностей между прогнозируемыми значениями и фактическими значениями. | $ ∑(фактическое\ значение - прогнозируемое\ значение)^2 $ |
| Среднеквадратическая ошибка (MSE) | Среднее значение потерь L2 для набора из N примеров. | $ \frac{1}{N} ∑ (фактическое\ значение - прогнозируемое\ значение)^2 $ |
| Среднеквадратическая ошибка (RMSE) | Квадратный корень из средней квадратической ошибки (СКО). | $ \sqrt{\frac{1}{N} ∑ (фактическое\ значение - прогнозируемое\ значение)^2} $ |
Функциональное различие между потерями L1 и L2 (или между MAE/RMSE и MSE) заключается в возведении в квадрат. Когда разница между прогнозом и меткой велика, возведение в квадрат ещё больше увеличивает потерю. Когда разница мала (меньше 1), возведение в квадрат ещё меньше.
Метрики потерь, такие как MAE и RMSE, могут быть предпочтительнее потерь L 2 или MSE в некоторых случаях использования, поскольку они, как правило, более понятны для человеческого восприятия, поскольку они измеряют ошибку, используя ту же шкалу, что и прогнозируемое значение модели.
При обработке нескольких примеров одновременно мы рекомендуем усреднять потери по всем примерам, используя MAE, MSE или RMSE.
Пример расчета убытков
Используя предыдущую линию наилучшего соответствия , мы рассчитаем потерю L2 для одного примера. Из линии наилучшего соответствия мы получили следующие значения веса и смещения:
- $ \small{Вес: -4,6} $
- $ \small{Смещение: 34} $
Если модель предсказывает, что автомобиль весом 2370 фунтов проезжает 23,1 мили на галлон, но на самом деле он проезжает 26 миль на галлон, мы рассчитаем потерю L 2 следующим образом:
| Ценить | Уравнение | Результат |
|---|---|---|
| Прогноз | $\small{смещение + (вес * признак\ значение)}$ $\small{34 + (-4,6*2,37)}$ | $\small{23.1}$ |
| Фактическое значение | $ \small{лейбл} $ | $ \small{ 26 } $ |
| потеря L 2 | $ \small{ (фактическое\ значение - прогнозируемое\ значение)^2 } $ $\small{ (26 - 23.1)^2 }$ | $\small{8.41}$ |
В этом примере потеря L 2 для этой единственной точки данных составляет 8,41.
Выбирая проигрыш
Решение об использовании MAE или MSE может зависеть от набора данных и того, как вы хотите обрабатывать некоторые прогнозы. Большинство значений признаков в наборе данных обычно попадают в определённый диапазон. Например, автомобили обычно весят от 2000 до 5000 фунтов и расходуют от 8 до 50 миль на галлон. Автомобиль весом 8000 фунтов или с расходом 100 миль на галлон выходит за рамки типичного диапазона и будет считаться выбросом .
Выбросом также может считаться то, насколько сильно предсказания модели отличаются от реальных значений. Например, вес автомобиля весом 3000 фунтов (1360 кг) находится в диапазоне типичного веса автомобиля, а расход топлива 40 миль на галлон (40 миль на галлон) — в диапазоне типичной топливной экономичности. Однако автомобиль весом 3000 фунтов (1360 кг), проезжающий 40 миль на галлон (40 миль на галлон), будет выбросом с точки зрения прогноза модели, поскольку модель предсказывает, что автомобиль весом 3000 фунтов (1360 кг) проедет около 20 миль на галлон (20 миль на галлон).
При выборе оптимальной функции потерь учитывайте, как модель должна обрабатывать выбросы. Например, MSE приближает модель к выбросам, а MAE — нет. Потеря L2 влечет за собой гораздо более высокий штраф за выброс, чем потеря L1 . Например, на следующих изображениях показаны модель, обученная с использованием MAE, и модель, обученная с использованием MSE. Красная линия представляет собой полностью обученную модель, которая будет использоваться для прогнозирования. Выбросы ближе к модели, обученной с использованием MSE, чем к модели, обученной с использованием MAE.
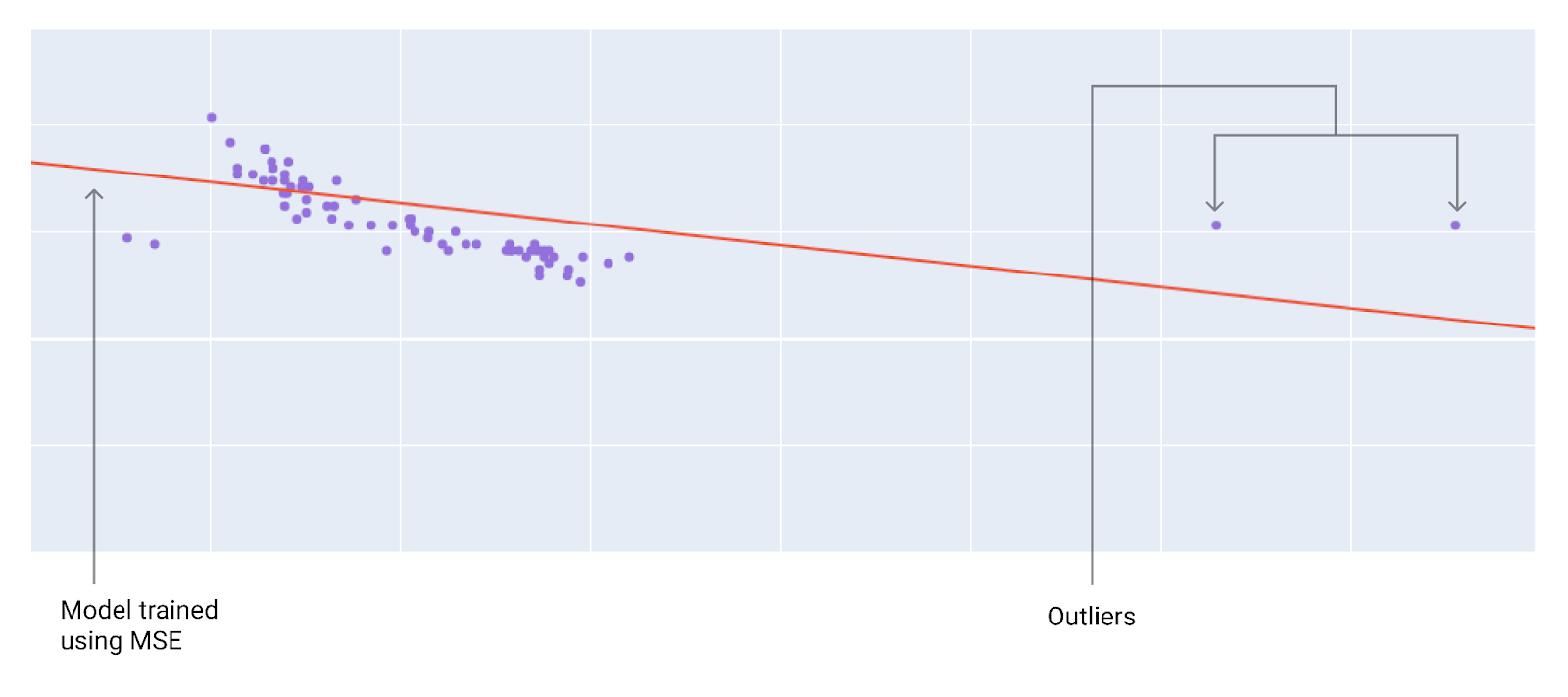
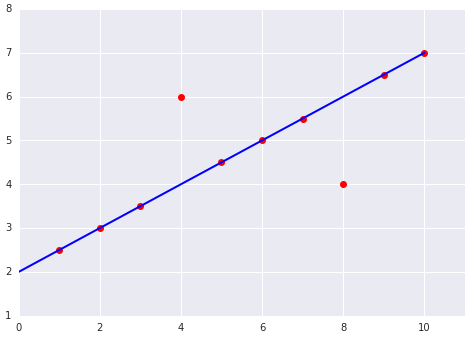
Рисунок 9. Потеря MSE приближает модель к выбросам.
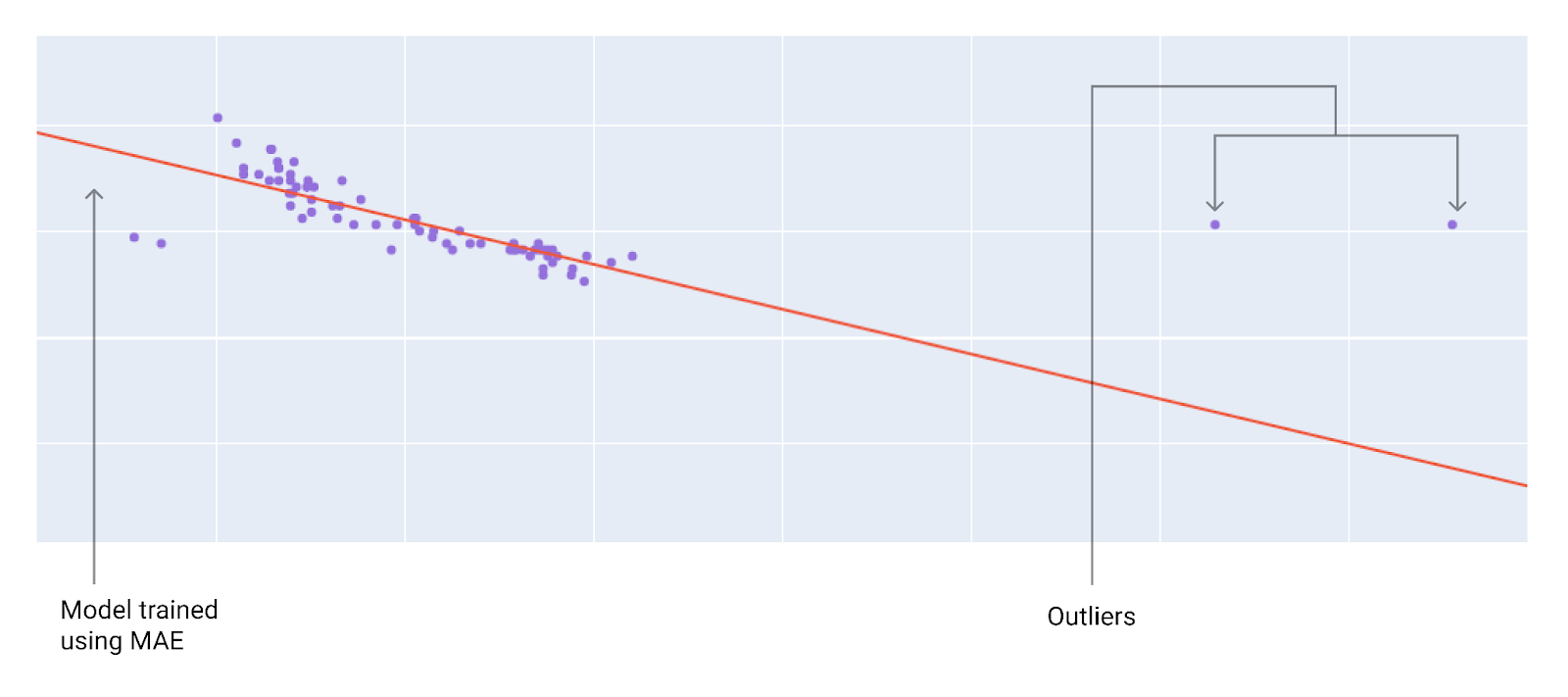
Рисунок 10. Потеря MAE позволяет модели оставаться дальше от выбросов.
Обратите внимание на связь между моделью и данными:
Среднеквадратическая ошибка (MSE) . Модель ближе к выбросам, но дальше от большинства других точек данных.
MAE . Модель дальше от выбросов, но ближе к большинству других точек данных.
Проверьте свое понимание
Рассмотрим следующие два графика линейной модели, соответствующей набору данных:
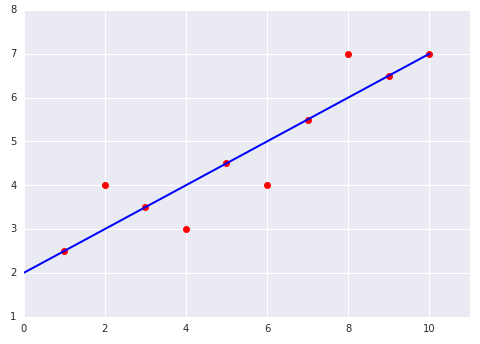 |  |
