В этом модуле рассматриваются концепции линейной регрессии .
Линейная регрессия — это статистический метод, используемый для поиска взаимосвязи между переменными. В контексте машинного обучения линейная регрессия находит взаимосвязь между признаками и меткой .
Например, предположим, что мы хотим спрогнозировать топливную экономичность автомобиля в милях на галлон на основе его веса, и у нас есть следующий набор данных:
| Фунты в тысячах (репортаж) | Миль на галлон (маркировка) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
Если мы нанесем эти точки на график, то получим следующий график:
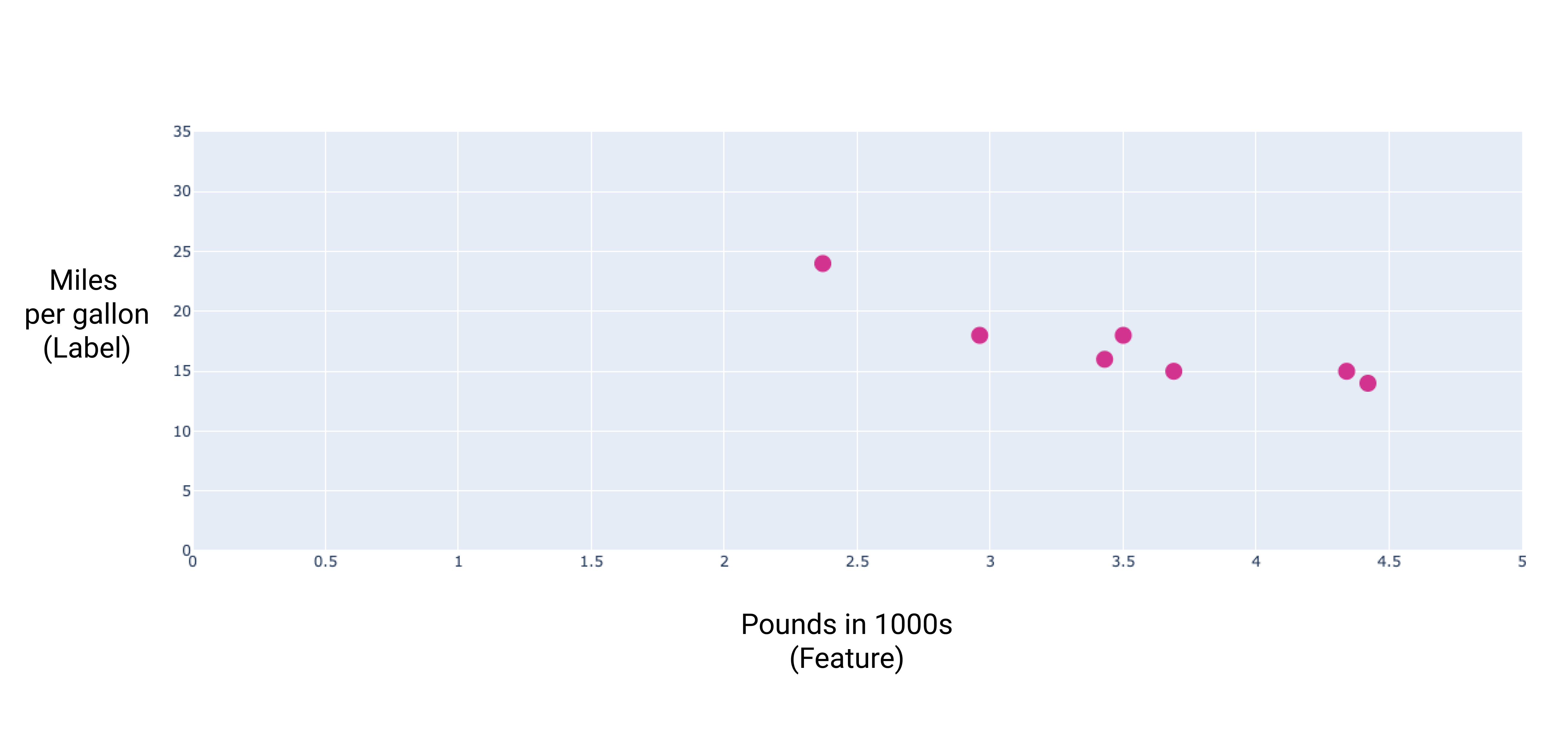
Рисунок 1. Вес автомобиля (в фунтах) в зависимости от пробега в милях на галлон. По мере увеличения веса автомобиля его пробег в милях на галлон, как правило, снижается.
Мы могли бы создать собственную модель, проведя линию наилучшего соответствия через точки:
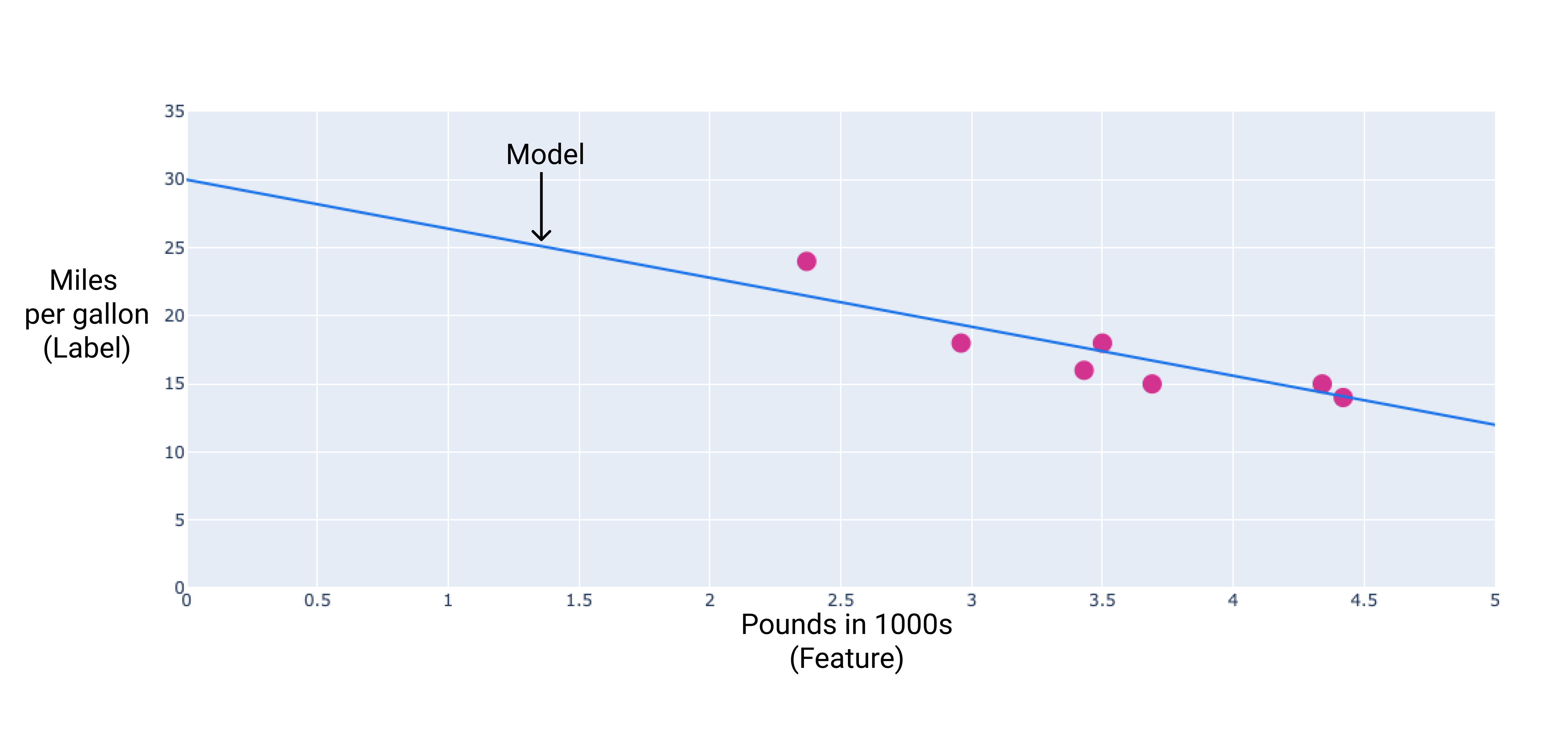
Рисунок 2. Линия наилучшего соответствия, проведенная через данные из предыдущего рисунка.
Уравнение линейной регрессии
В алгебраических терминах модель будет определяться как $ y = mx + b $, где
- $ y $ — это мили на галлон — значение, которое мы хотим предсказать.
- $ m $ — наклон прямой.
- $ x $ — это фунты (наше входное значение).
- $ b $ - точка пересечения с осью y.
В ML мы записываем уравнение для модели линейной регрессии следующим образом:
где:
- $ y' $ — прогнозируемая метка — выход.
- $ b $ — это смещение модели. Смещение — это то же самое понятие, что и пересечение с осью Y в алгебраическом уравнении для прямой. В машинном обучении смещение иногда обозначается как $ w_0 $. Смещение — это параметр модели, рассчитываемый в процессе обучения.
- $w_1$ — это вес признака. Вес — это то же самое понятие, что и наклон $m$ в алгебраическом уравнении прямой. Вес — это параметр модели, который рассчитывается в процессе обучения.
- $ x_1 $ — это признак — входные данные.
В процессе обучения модель рассчитывает вес и смещение, которые позволяют получить наилучшую модель.
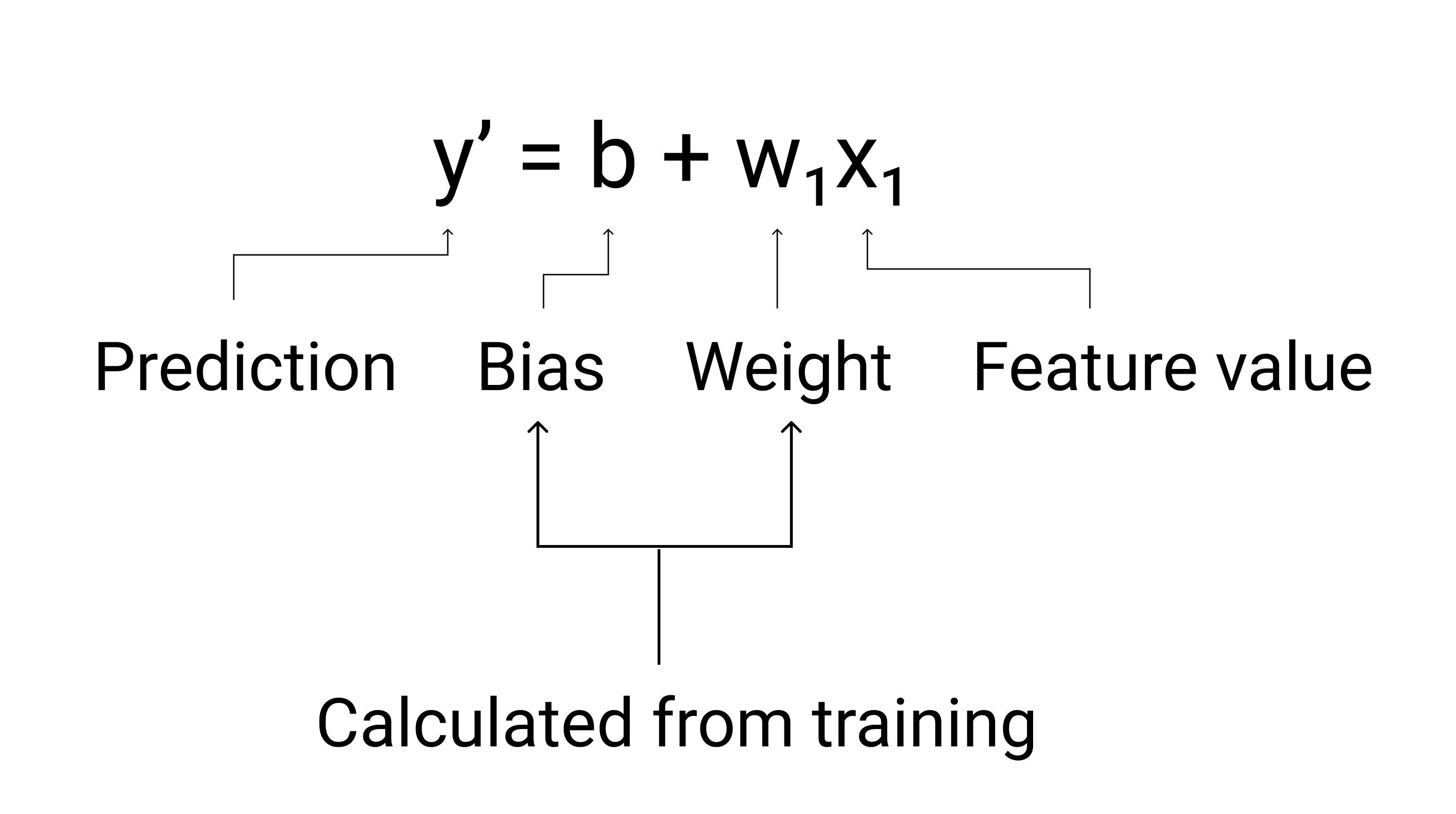
Рисунок 3. Математическое представление линейной модели.
В нашем примере мы рассчитаем вес и смещение по нарисованной нами линии. Смещение равно 34 (точка пересечения линии с осью Y), а вес равен –4,6 (наклон линии). Модель будет определена как $ y' = 34 + (-4,6)(x_1) $, и мы сможем использовать её для прогнозирования. Например, используя эту модель, автомобиль весом 4000 фунтов (1800 кг) будет иметь прогнозируемую топливную экономичность 15,6 миль на галлон (24,7 км/галлон).
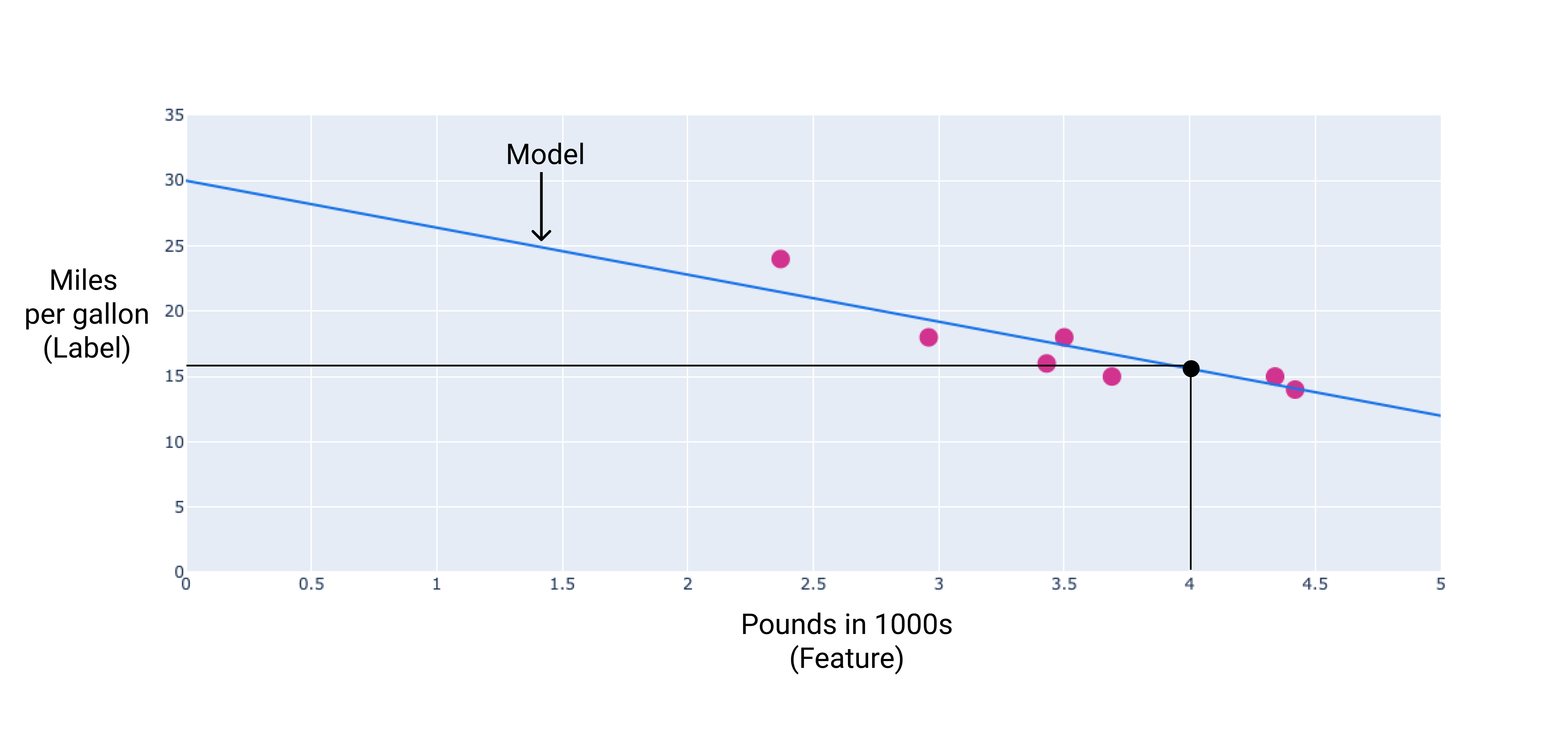
Рисунок 4. Используя эту модель, автомобиль весом 4000 фунтов имеет прогнозируемую топливную экономичность 15,6 миль на галлон.
Модели с множеством функций
Хотя в примере в этом разделе используется только одна характеристика — вес автомобиля, более сложная модель может опираться на несколько характеристик, каждая из которых имеет свой вес ($ w_1 $, $ w_2 $ и т. д.). Например, модель, опирающаяся на пять характеристик, будет записана следующим образом:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Например, модель, прогнозирующая расход топлива, может дополнительно использовать такие функции, как:
- Объем двигателя
- Ускорение
- Количество цилиндров
- Лошадиная сила
Эта модель будет записана следующим образом:
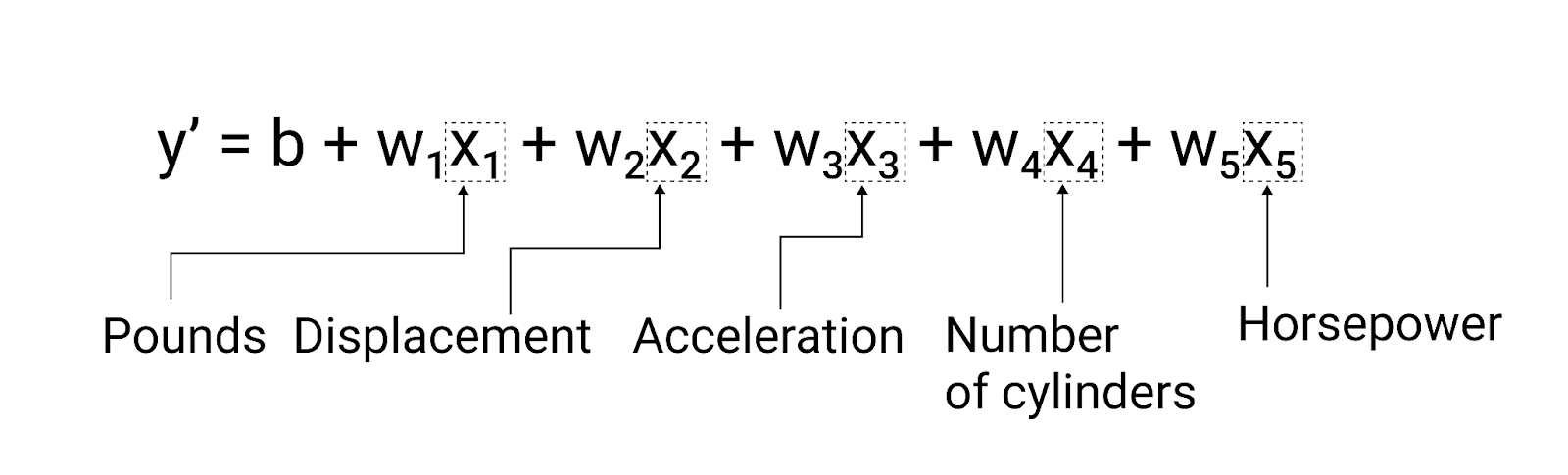
Рисунок 5. Модель с пятью характеристиками для прогнозирования пробега автомобиля на галлон.
Построив график нескольких дополнительных характеристик, мы можем увидеть, что они также имеют линейную зависимость от значения на этикетке — миль на галлон:
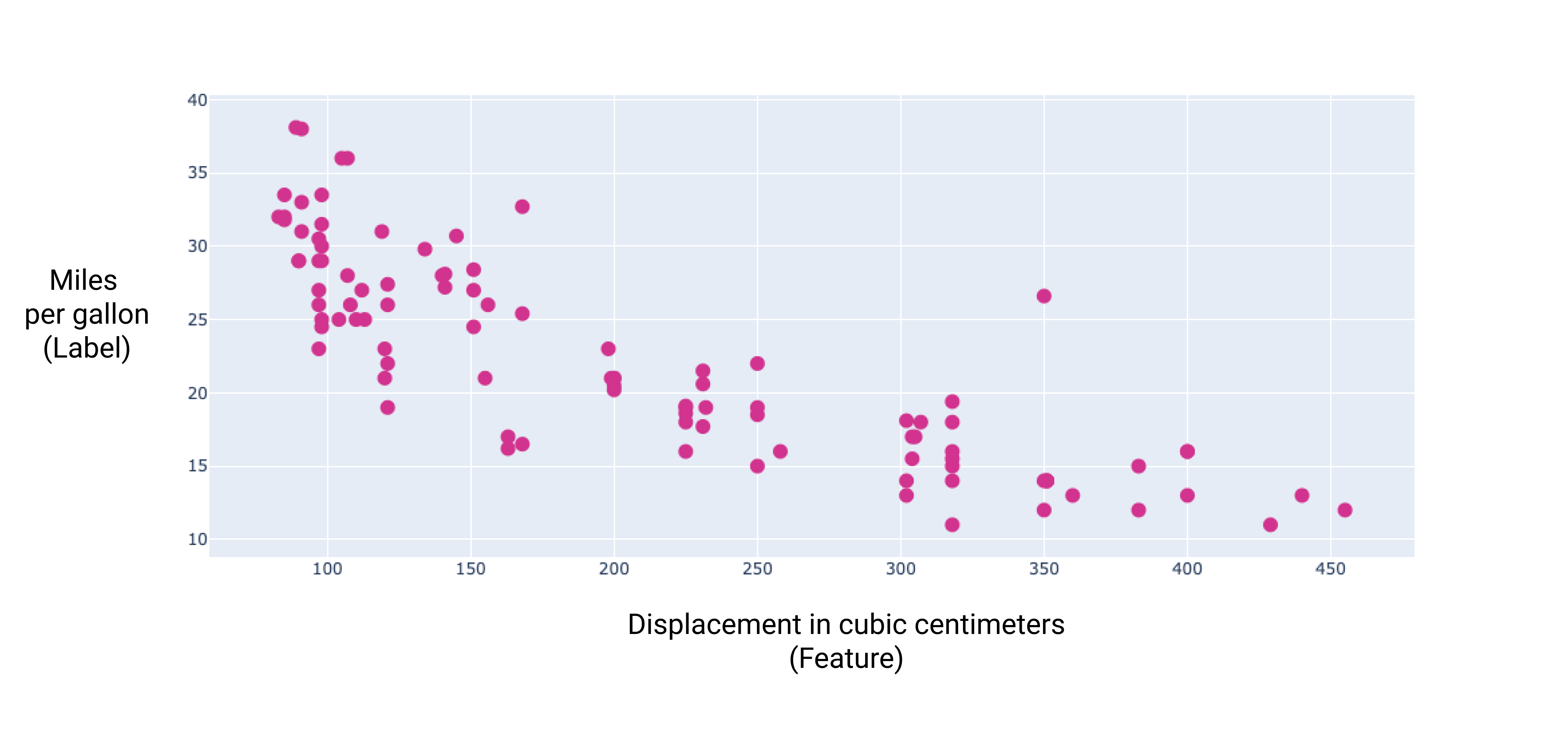
Рисунок 6. Объём двигателя автомобиля в кубических сантиметрах и его расход топлива в милях на галлон. По мере увеличения объёма двигателя автомобиля его расход топлива в милях на галлон, как правило, снижается.
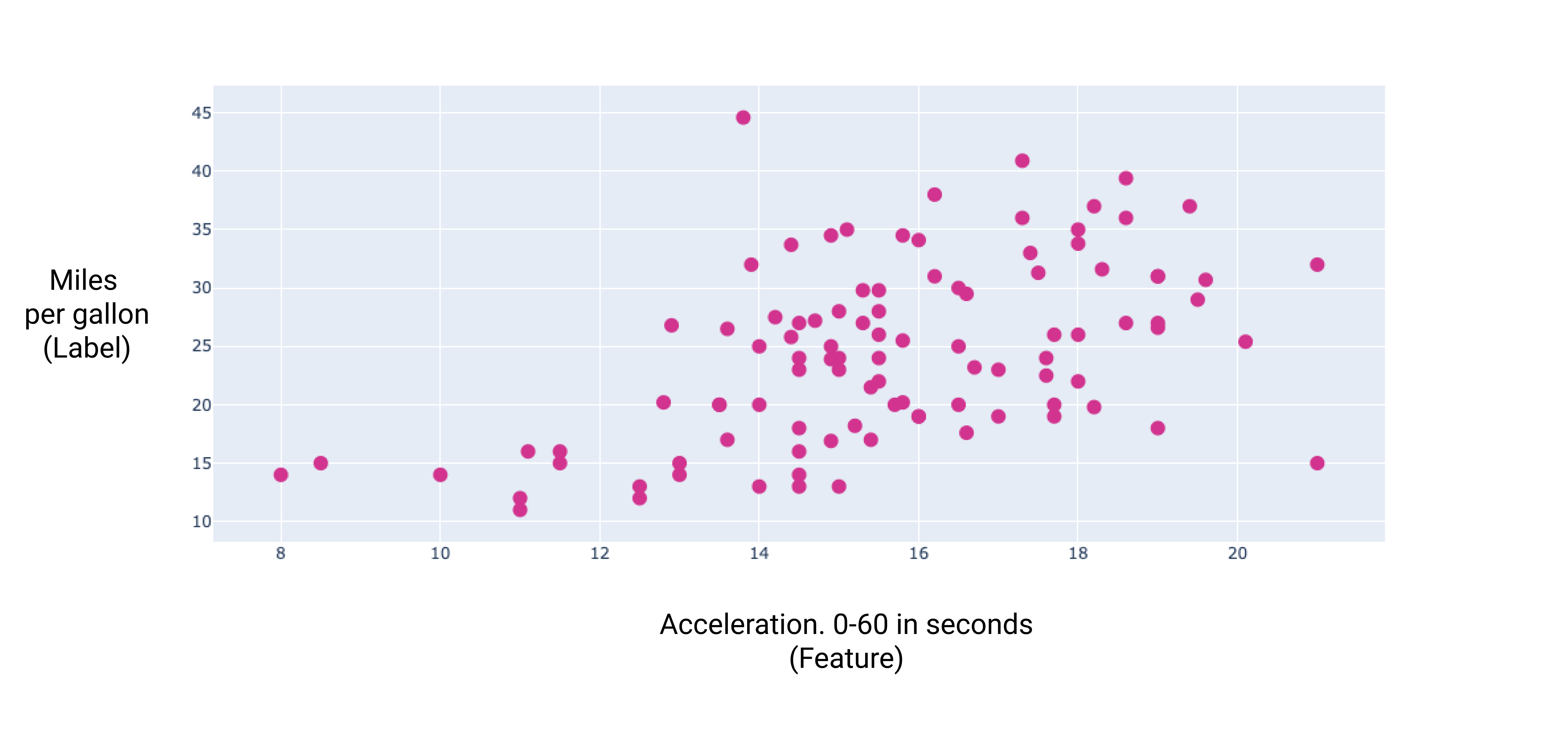
Рисунок 7. Ускорение автомобиля и его расход топлива. Чем дольше автомобиль разгоняется, тем выше расход топлива.
