Втрати – це числовий метрика, що описує, наскільки прогнози моделі помилкові. Втрати вимірюють відстань між прогнозами моделі й фактичними мітками. Мета навчання моделі – мінімізувати втрати, знизити їх до найменшого можливого значення.
На рисунку, наведеному нижче, втрати зображено як стрілки, проведені від точок даних до моделі. Стрілки показують, наскільки далеко прогнозовані значення моделі від фактичних.
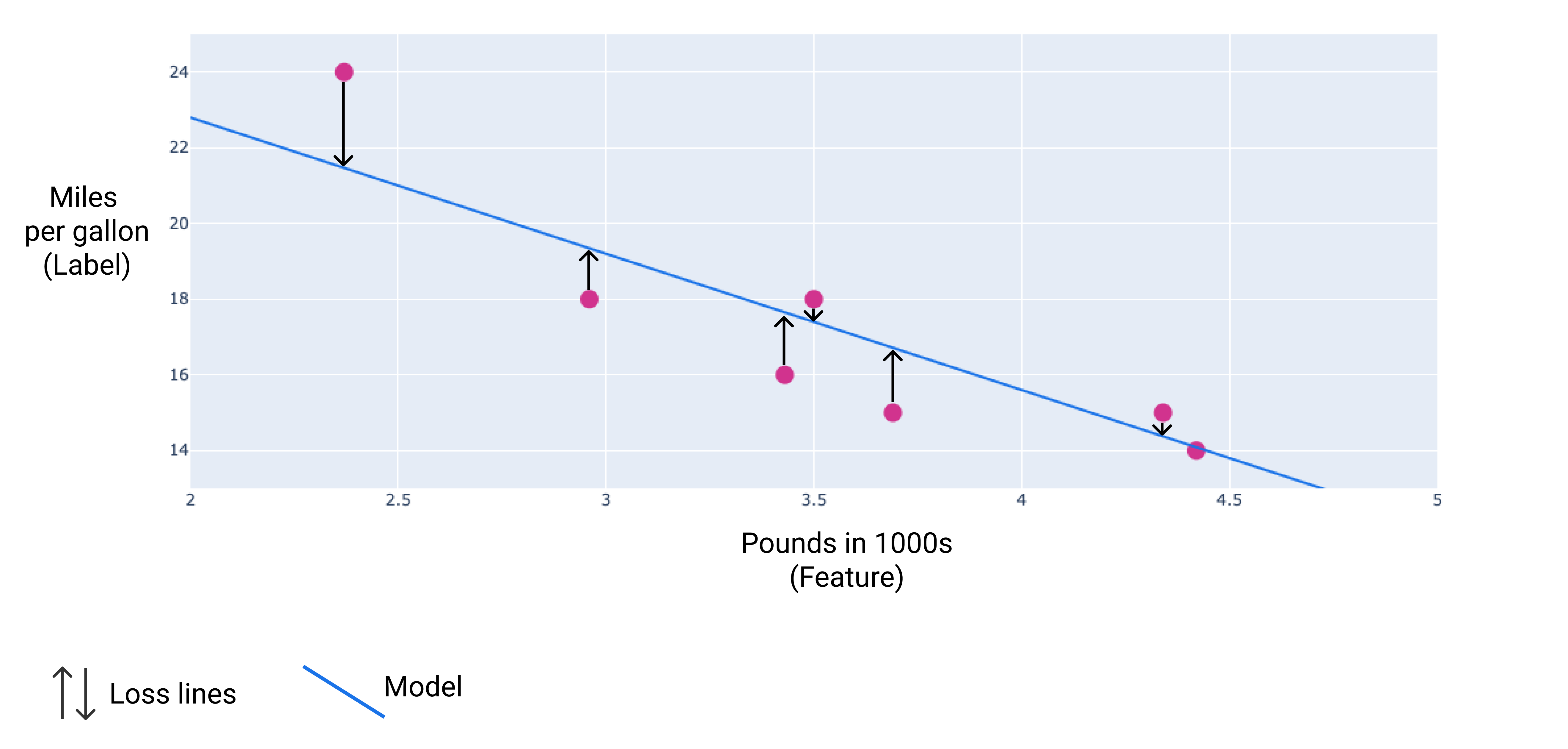
Рисунок 9. Втрати вимірюються від фактичного значення до прогнозованого значення.
Відстань втрат
У статистиці й машинному навчанні втрати – це різниця між прогнозованими й фактичними значеннями. Ця метрика – саме відстань між значеннями, а не на напрямок. Наприклад, якщо прогноз моделі – число 2, а фактичне значення дорівнює 5, не важливо, що втрата від’ємна $ –3 $ ($ 2 – 5 = –3 $). Натомість важливо те, що відстань між значеннями становить $ 3 $. Тому в усіх методах розрахунку втрат знак вилучається.
Два найпоширеніші способи вилучення знака:
- взяти модуль різниці фактичного значення й прогнозу;
- вирахувати квадрат різниці фактичного значення й прогнозу.
Типи втрат
У лінійній регресії є чотири основні типи втрат, їх наведено в таблиці нижче.
| Тип втрат | Визначення | Формула |
|---|---|---|
| Втрати L1 | Сума модулів різниць прогнозованих і фактичних значень. | $ ∑ | фактичне\ значення – прогнозоване\ значення| $ |
| Середня абсолютна похибка (MAE) | Середнє значення втрат L1 у наборі прикладів. | $ \frac{1}{N} ∑ | фактичне\ значення – прогнозоване\ значення | $ |
| Втрати L2 | Сума квадратів різниць прогнозованих і фактичних значень. | $ ∑(фактичне\ значення – прогнозоване\ значення)^2 $ |
| Середньоквадратична похибка (MSE) | Середнє значення втрат L2 в наборі прикладів. | $ \frac{1}{N} ∑ (фактичне\ значення – прогнозоване\ значення)^2 $ |
Функціональна різниця між втратами L1 і втратами L2 (або між MAE й MSE) – піднесення до квадрата. Коли різниця між прогнозом і міткою велика, піднесення до квадрата робить втрати ще більшими. Коли різниця невелика (менша ніж 1), піднесення до квадрата робить втрати ще меншими.
Якщо ви обробляєте кілька прикладів одночасно, рекомендуємо усереднювати втрати для них усіх, незалежно від того, використовується MAE чи MSE.
Приклад розрахунку втрат
Використовуючи попередню лінію найкращої відповідності, ми обчислимо втрати L2 для одного прикладу. На основі лінії найкращої відповідності отримано значення ваги й зсуву, указані нижче.
- $ \small{Вага: –3,6} $
- $ \small{Зсув: 30} $
Якщо модель прогнозує, що результат для автомобіля вагою 2370 фунтів становитиме 21,5 милі на галон, але фактичний результат – це 24 милі на галон, втрати L2 можна розрахувати так, як показано нижче.
| Значення | Формула | Результат |
|---|---|---|
| Прогноз | $\small{зсув + (вага * значення\ ознаки)}$ $\small{30 + (–3,6 * 2,37)}$ |
$\small{21,5}$ |
| Фактичне значення | $ \small{ мітка } $ | $ \small{ 24 } $ |
| Втрати L2 | $ \small{ (прогноз – фактичне\ значення)^2} $ $\small{ (21,5 – 24)^2 }$ |
$\small{6,25}$ |
У цьому прикладі втрати L2 для вказаної однієї точки даних становлять 6,25.
Як вибрати тип втрат
Рішення використовувати MAE чи MSE може залежати від набору даних і способу обробки певних прогнозів. Більшість значень ознак із набору даних зазвичай у межах чіткого діапазону. Наприклад, автомобілі зазвичай важать від 2000 до 5000 фунтів і проходять від 8 до 50 миль на галон. Автомобіль вагою 8000 фунтів чи той, що проходить 100 миль на галон, не є в межах типового діапазону й вважається викидом.
Викид також може вказувати на те, наскільки сильно прогнози моделі відрізняються від реальних значень. Наприклад, автомобіль вагою 3000 фунтів або той, що проходить 40 миль на галон, знаходиться в межах типових діапазонів. Однак автомобіль вагою 3000 фунтів, який проходить 40 миль на галон, буде викидом з погляду прогнозу моделі, тому що вона передбачає, що такий автомобіль проходить від 18 до 20 миль на галон.
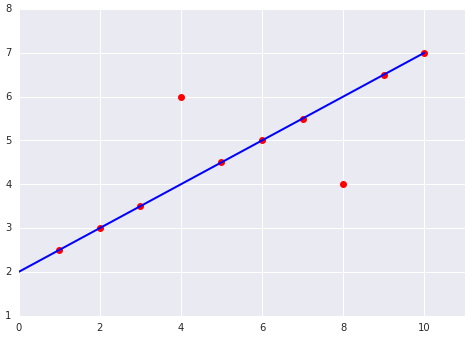
Вибираючи оптимальну функцію втрат, подумайте, як моделі слід обробляти викиди. Наприклад, MSE наближує модель ближче до викидів, тоді як MAE – ні. Втрати L2 тягнуть за собою набагато більший штраф за викид, ніж втрати L1. Наприклад, на зображеннях нижче показано дві моделі, одна з яких навчалася з використанням MAE, а інша – із застосуванням MSE. Червона лінія позначає повністю навчену модель, яка використовуватиметься для прогнозування. Викиди перебувають ближче до моделі, навченої з використанням MSE, ніж до тієї, для якої було застосовано MAE.
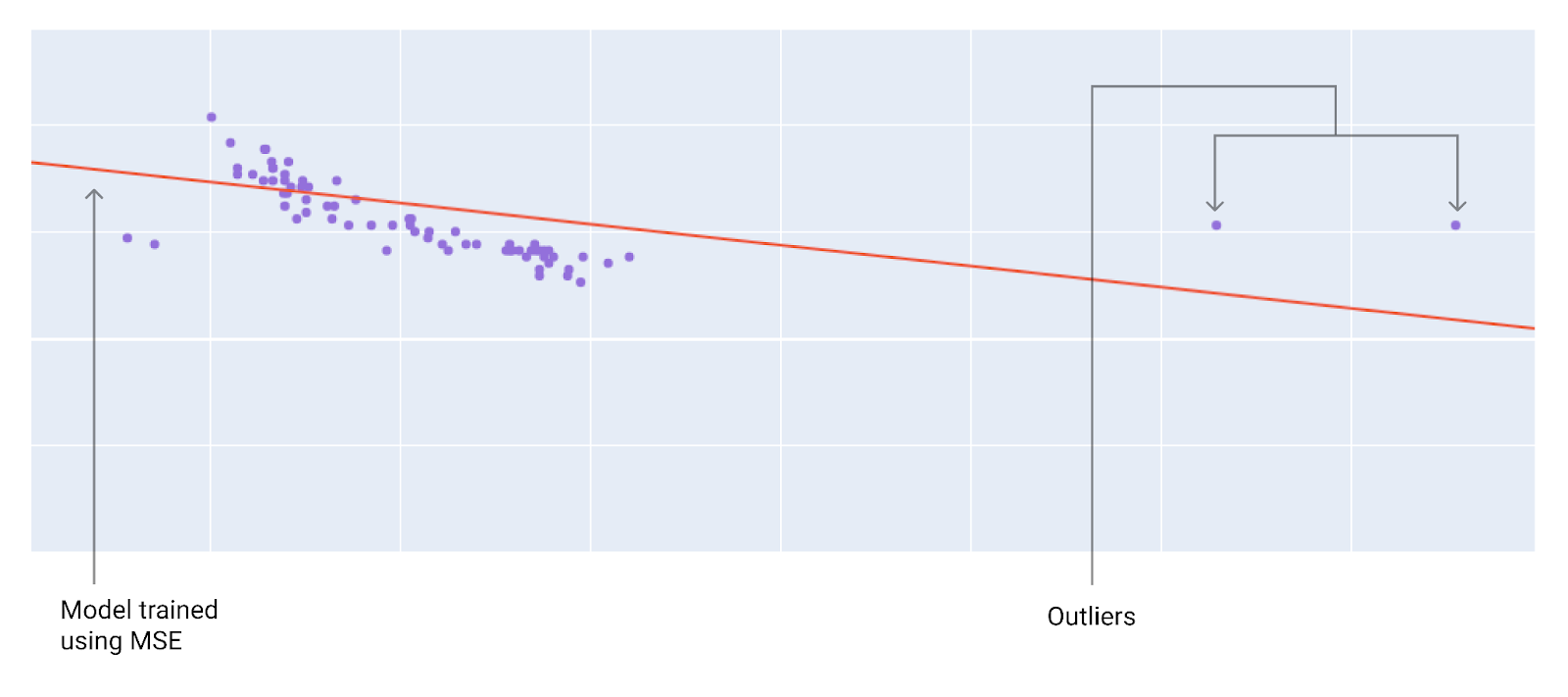
Рисунок 10. Модель, навчена з використанням MSE, проходить ближче до викидів.
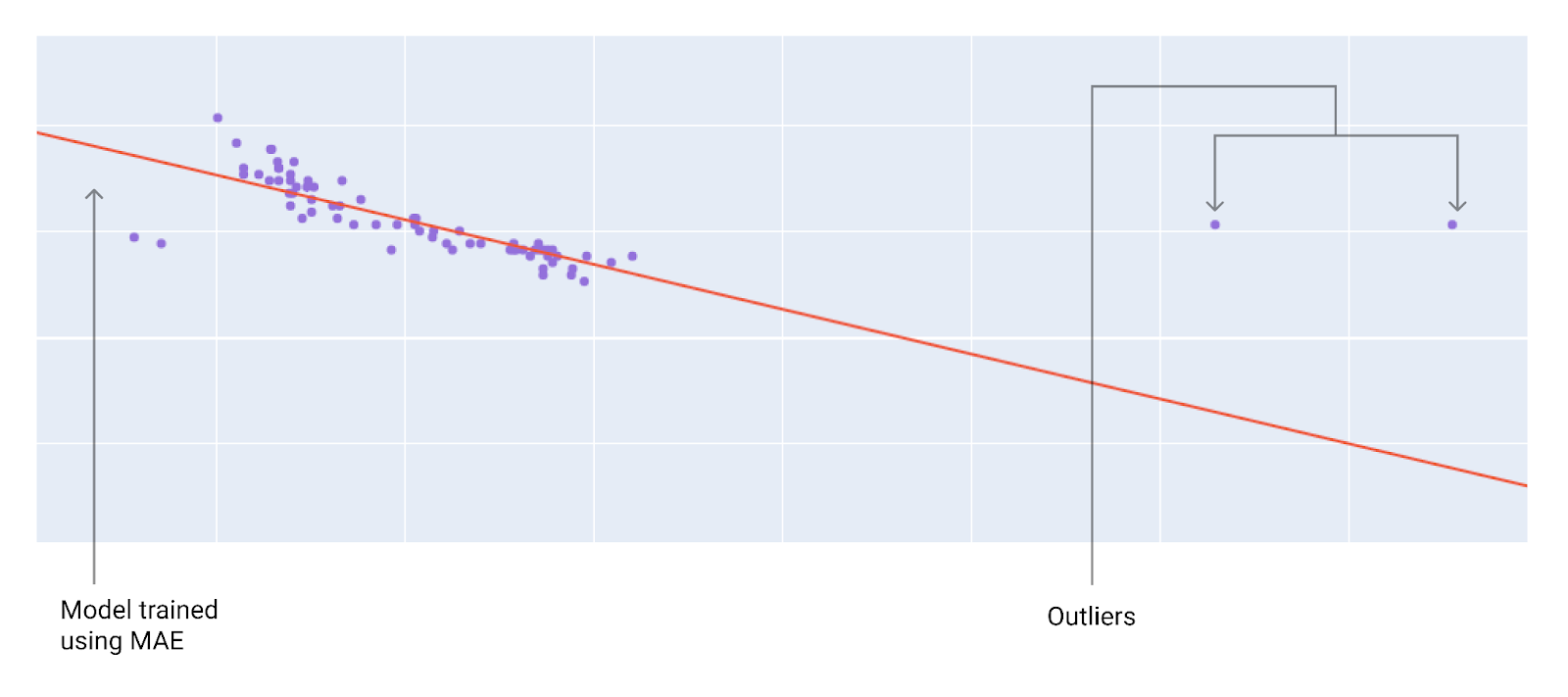
Рисунок 11. Модель, навчена з використанням MAE, проходить далі від викидів.
Зверніть увагу на зв’язок між моделлю й даними:
якщо використовується MSE, модель проходить ближче до викидів, але далі від більшості інших точок даних;
якщо використовується MAE, модель проходить далі від викидів, але ближче до більшості інших точок даних.
Перевірте свої знання
Розгляньмо дві діаграми, наведені нижче.
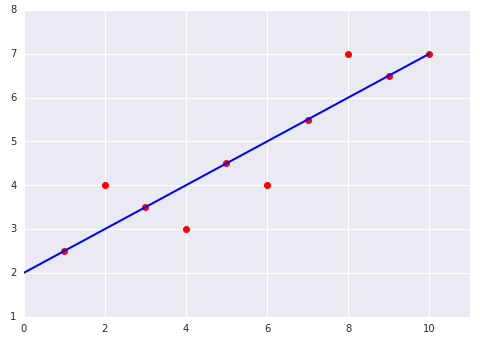
|
|