Modul ini memperkenalkan konsep regresi linear.
Regresi linear adalah teknik statistik yang digunakan untuk menemukan hubungan antarvariabel. Dalam ML Dalam konteks, regresi linear menemukan hubungan antara fitur dan label.
Misalnya, kita ingin memprediksi efisiensi bahan bakar mobil dalam mil per galon berdasarkan berat mobil, dan kita memiliki {i>dataset<i} berikut:
| Pound dalam 1000-an (fitur) | Mil per galon (label) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Jika kita memetakan poin-poin ini, kita akan mendapatkan grafik berikut:
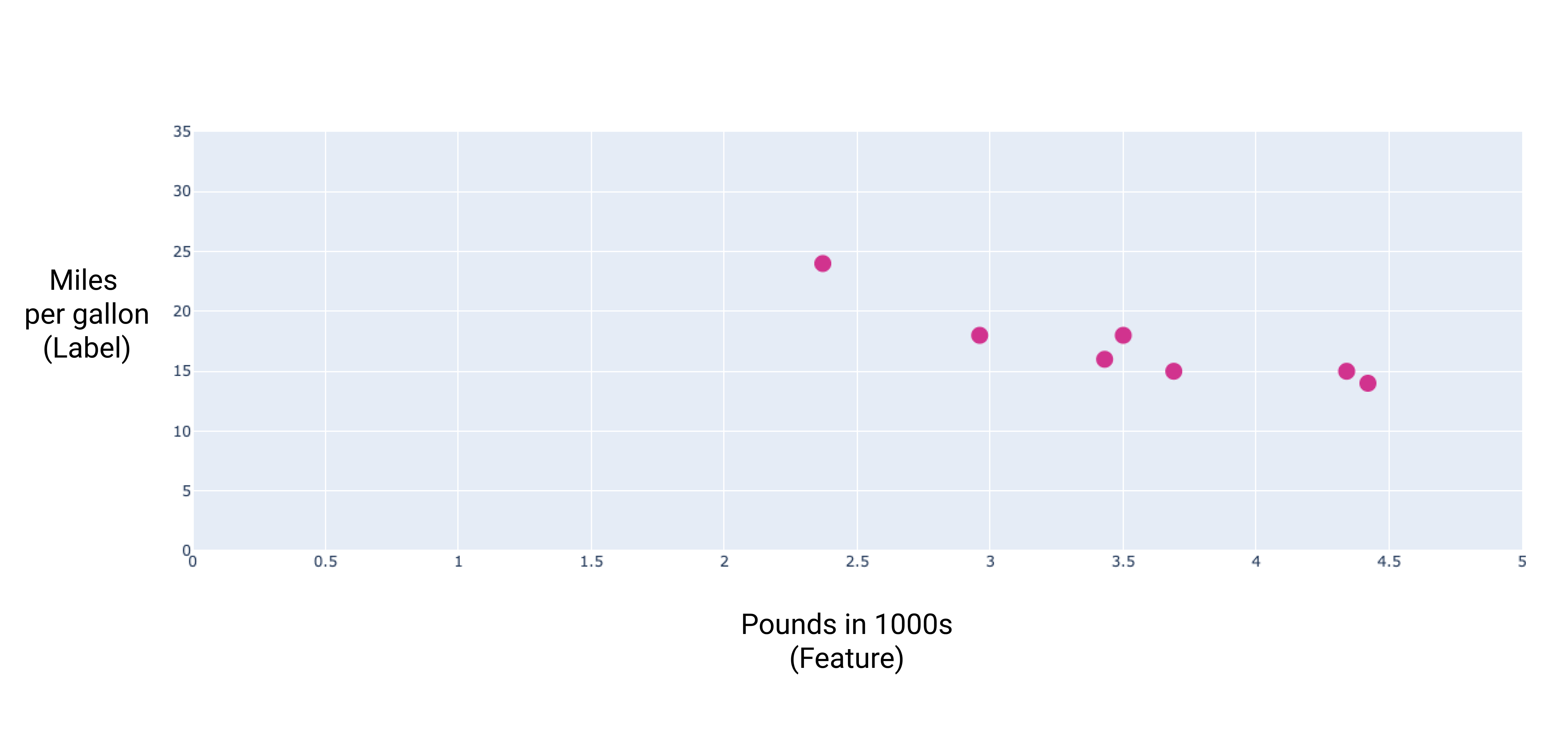
Gambar 1. Berat mobil (dalam pon) versus peringkat mil per galon. Sebagai seorang mobil menjadi lebih berat, peringkat mil per galonnya biasanya menurun.
Kita dapat membuat model sendiri dengan menggambar garis yang paling sesuai melalui titik-titik:
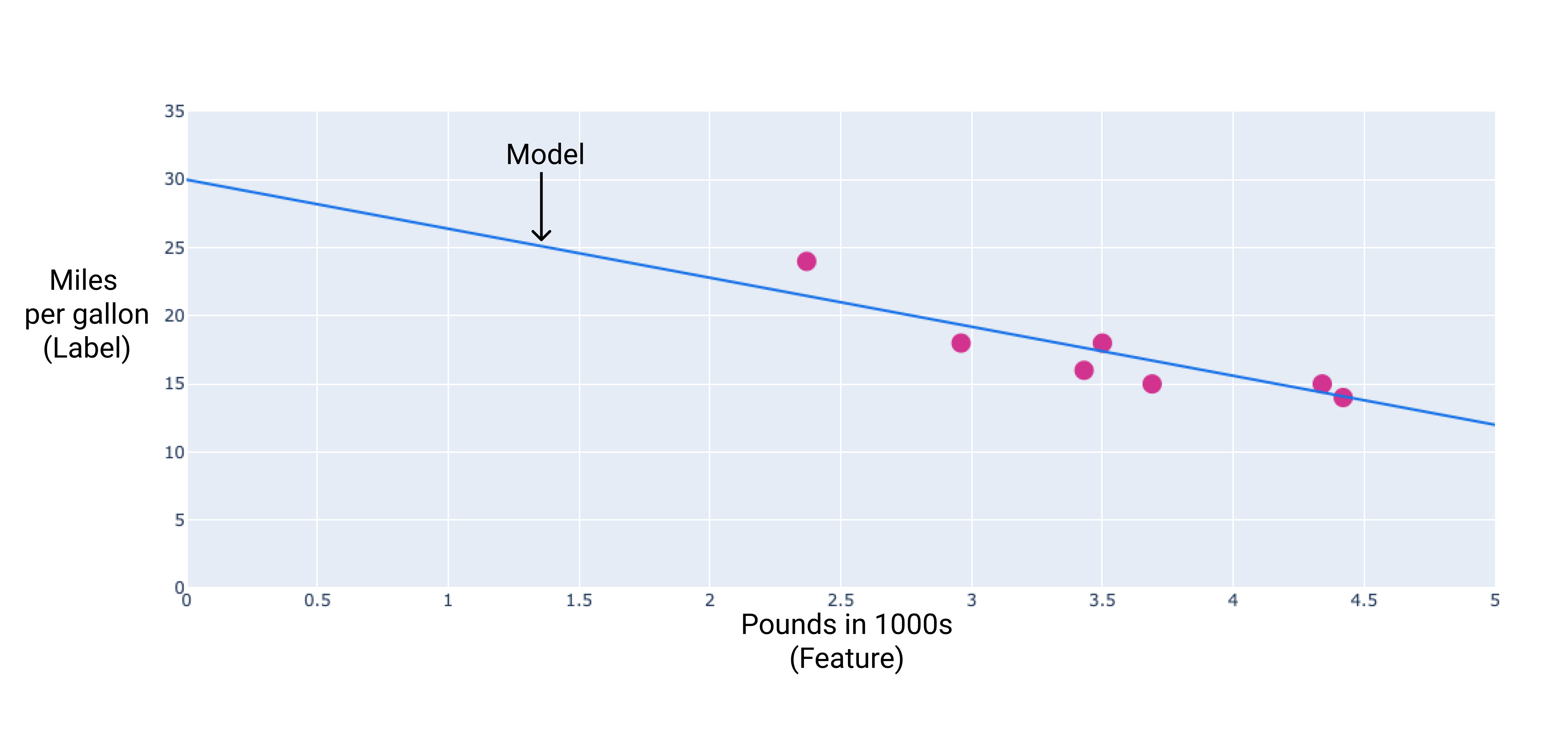
Gambar 2. Garis yang paling sesuai yang digambar melalui data dari gambar sebelumnya.
Persamaan regresi linear
Dalam istilah aljabar, model akan didefinisikan sebagai $ y = mx + b $, di mana
- $ y $ adalah mil per galon—nilai yang ingin kita prediksi.
- $ m $ adalah kemiringan garis.
- $ x $ adalah pound—nilai input kita.
- $ b $ adalah titik potong y.
Dalam ML, kita menulis persamaan untuk model regresi linear sebagai berikut:
dalam hal ini:
- $ y' $ adalah label yang diprediksi—output-nya.
- $ b $ adalah bias model. Bias adalah konsep yang sama dengan titik potong y dalam rumus aljabar persamaan untuk garis. Dalam ML, bias kadang-kadang disebut sebagai $ w_0 $. Bias merupakan parameter model dan dihitung selama pelatihan.
- $ w_1 $ adalah bobot dari aplikasi baru. Bobot adalah konsep yang sama dengan kemiringan $ m $ dalam aljabar persamaan untuk garis. Berat adalah parameter model dan yang dihitung selama pelatihan.
- $ x_1 $ adalah fitur— input teks.
Selama pelatihan, model menghitung bobot dan bias yang menghasilkan model transformer.
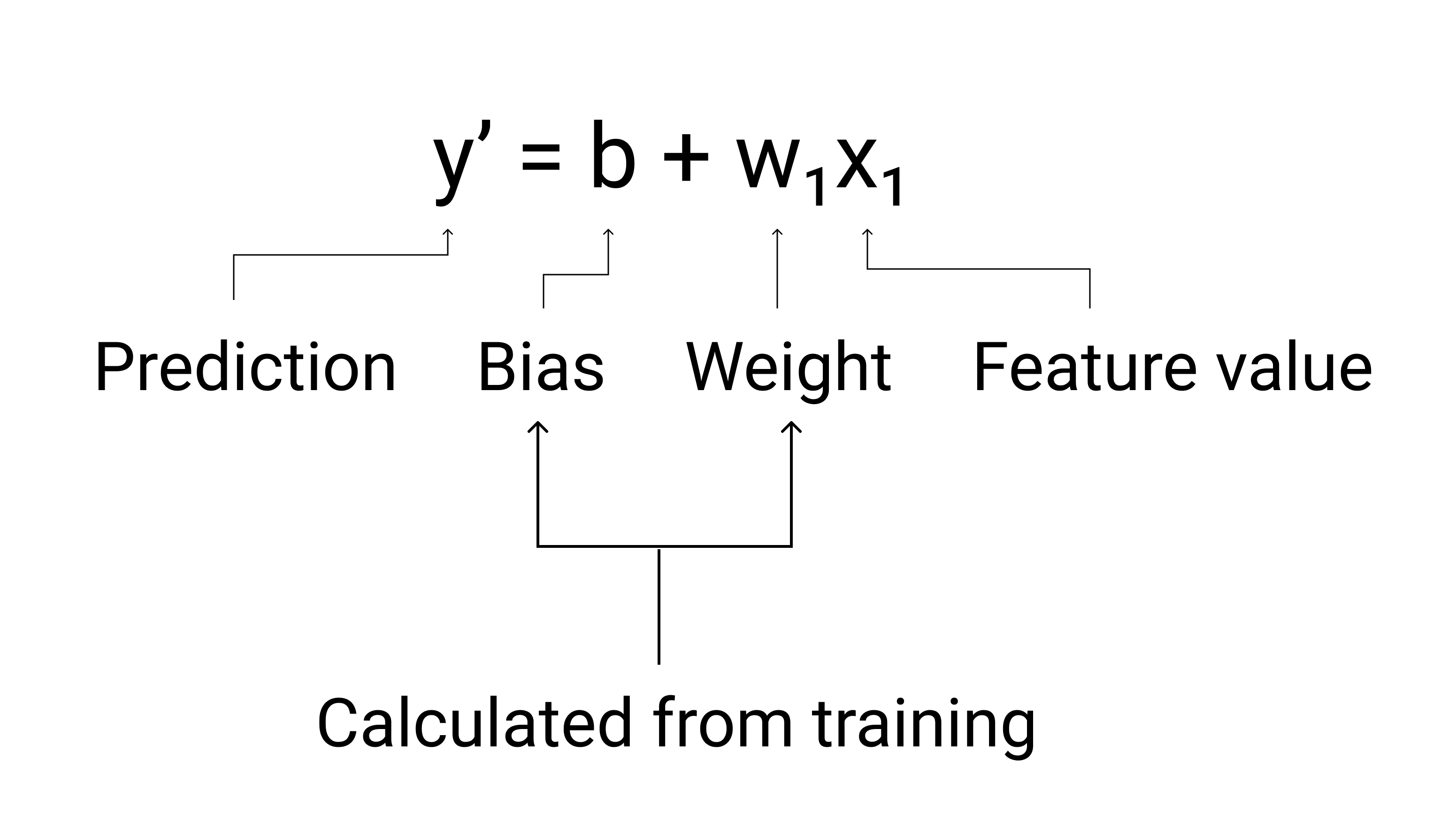
Gambar 3. Representasi matematika dari model linear.
Dalam contoh ini, kita akan menghitung bobot dan bias dari garis yang kita gambar. Tujuan bias adalah 30 (di mana garis berpotongan dengan sumbu y), dan bobotnya -3,6 ( kemiringan garis). Model ini akan didefinisikan sebagai $ y' = 30 + (-3,6)(x_1) $, dan kita bisa menggunakannya untuk membuat prediksi. Misalnya, dengan menggunakan model ini, Mobil seberat 4.000 pon akan memiliki efisiensi bahan bakar yang diperkirakan sebesar 15,6 mil per galon.
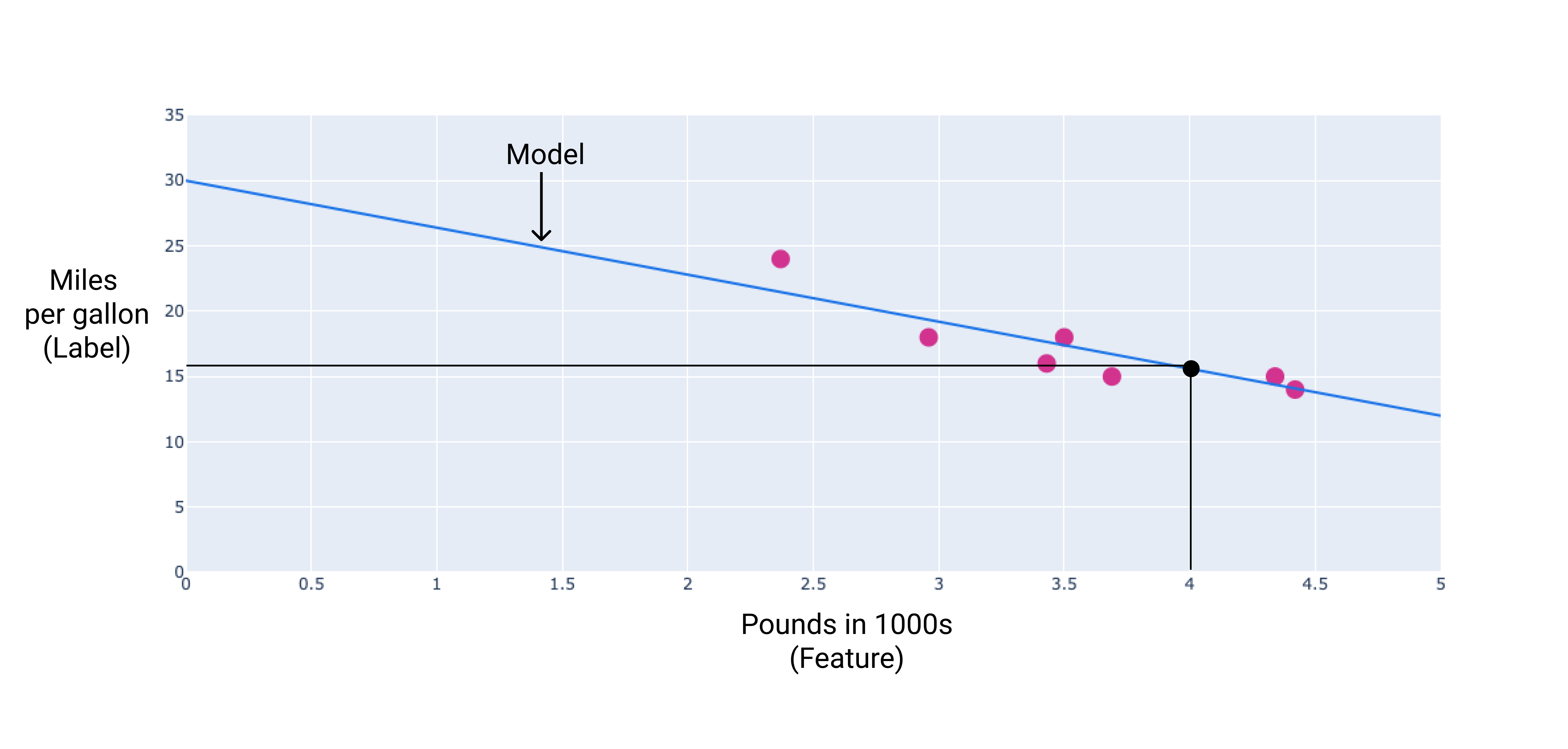
Gambar 4. Dengan menggunakan model, sebuah mobil seberat 4.000 pon memiliki prediksi efisiensi bahan bakar 15,6 mil per galon.
Model dengan berbagai fitur
Meskipun contoh di bagian ini hanya menggunakan satu fitur—ketinggian model yang lebih canggih mungkin mengandalkan beberapa fitur, masing-masing memiliki bobot terpisah ($ w_1 $, $ w_2 $, dll.). Misalnya, sebuah model yang bergantung pada lima fitur akan ditulis sebagai berikut:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Misalnya, model yang memprediksi jarak tempuh bensin juga dapat menggunakan fitur seperti berikut:
- Perpindahan mesin
- Akselerasi
- Jumlah silinder
- Daya kuda
Model ini akan ditulis sebagai berikut:
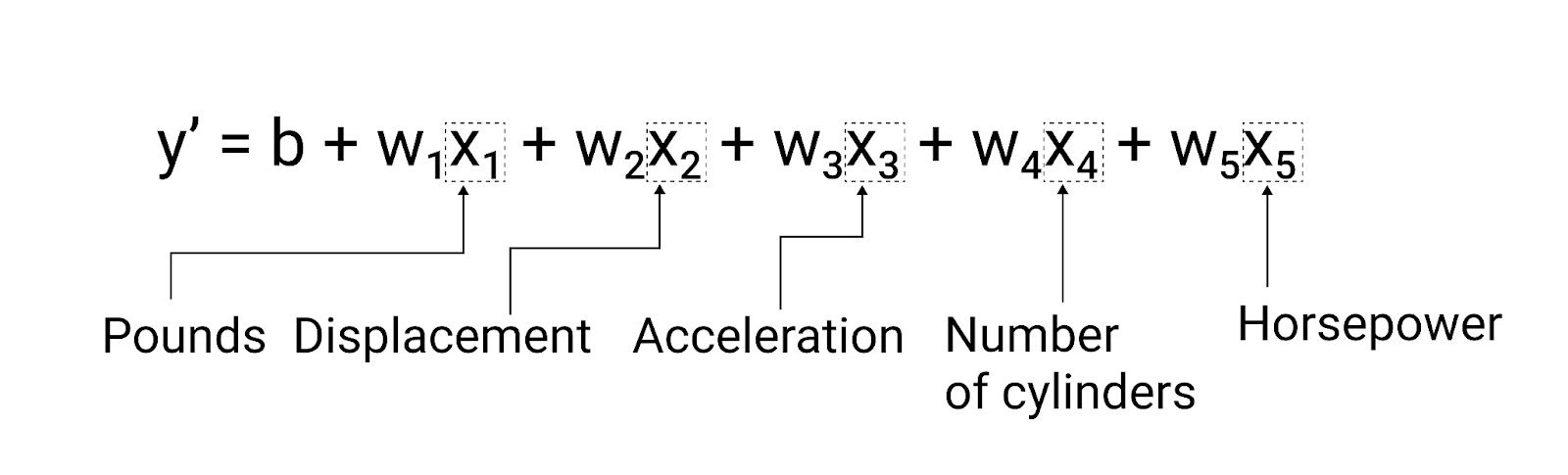
Gambar 5. Model dengan lima fitur untuk memprediksi mil per galon mobil rating.
Dengan membuat grafik dari beberapa fitur tambahan ini, kita dapat melihat bahwa mereka juga memiliki hubungan linear ke label, mil per galon:
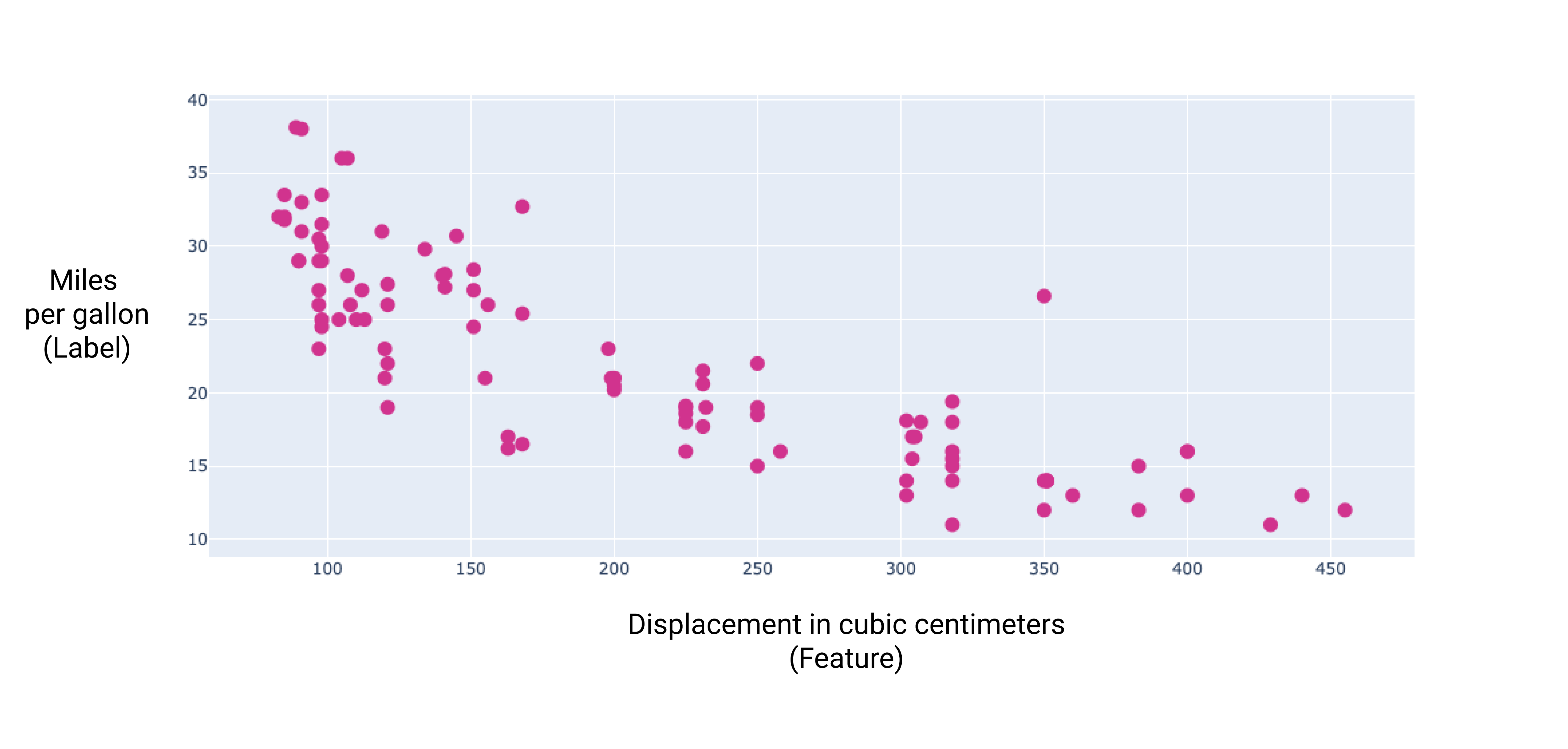
Gambar 6. Perpindahan mobil dalam sentimeter kubik dan mil per galonnya rating. Saat mesin mobil semakin besar, peringkat mil per galon umumnya menurun.
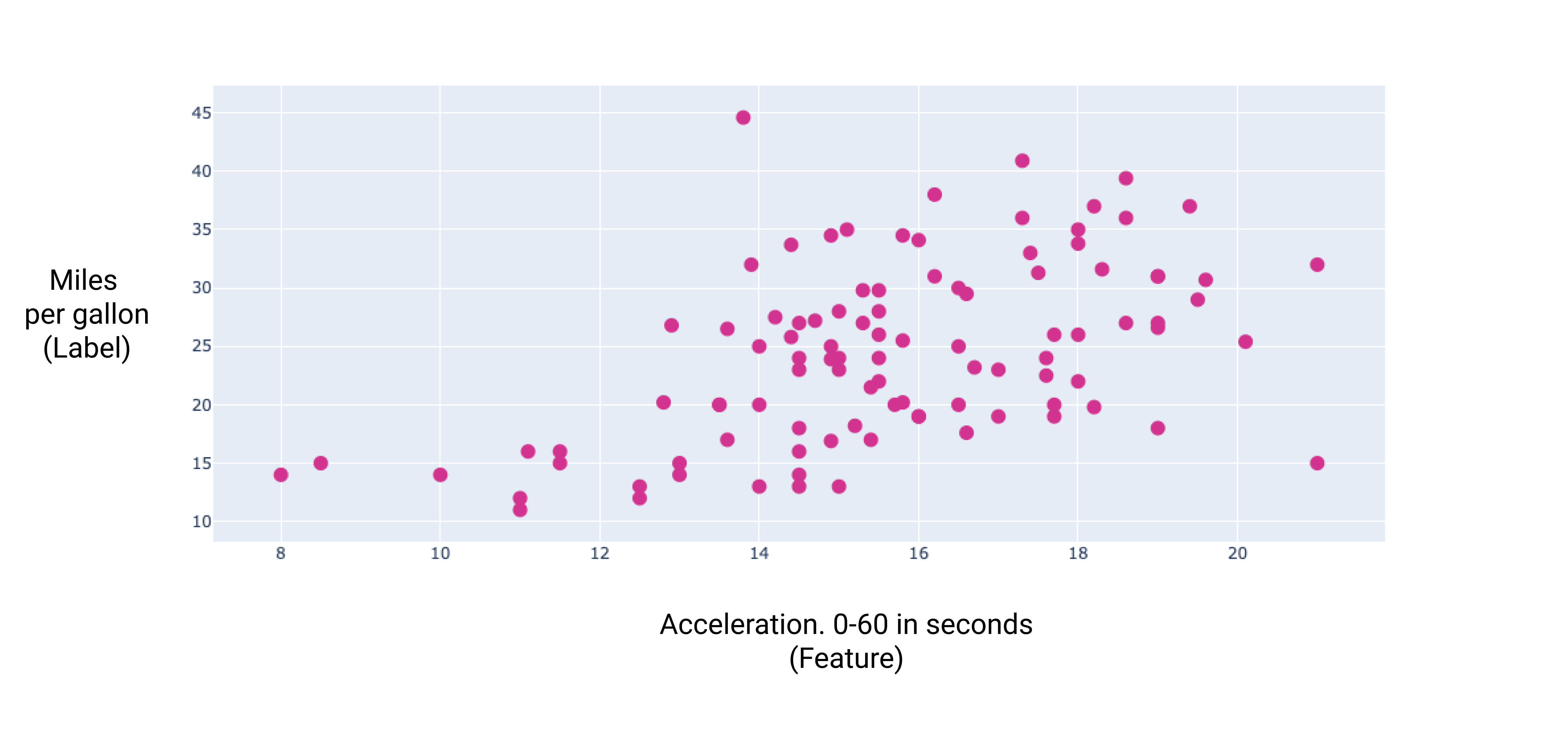
Gambar 7. Akselerasi mobil dan rating mil per galonnya. Sebagai akselerasi membutuhkan waktu lebih lama, peringkat mil per galon biasanya akan meningkat.
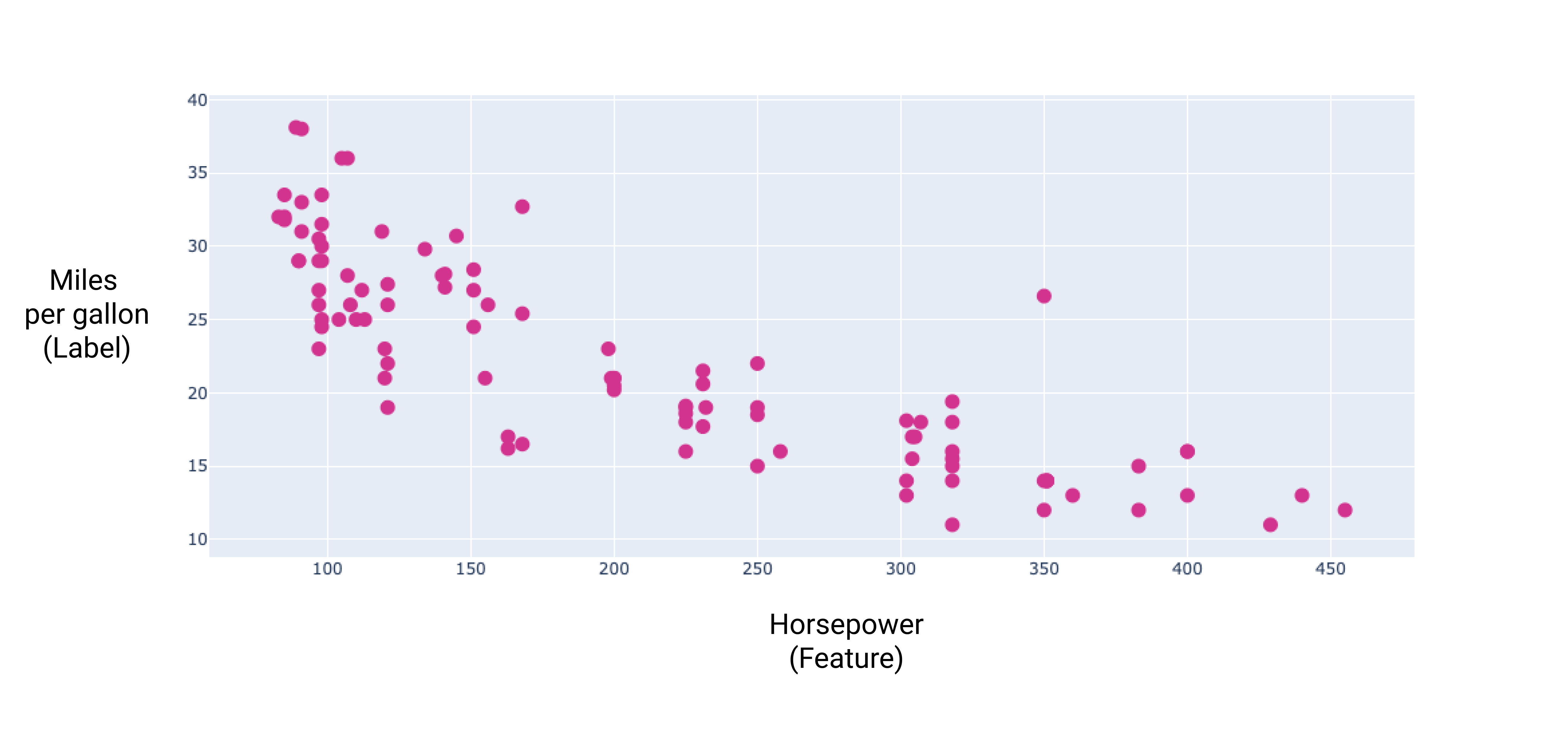
Gambar 8. Daya kuda mobil dan rating mil per galonnya. Sebagai tenaga kuda meningkat, peringkat mil per galon umumnya menurun.
