Questo modulo introduce i concetti di regressione lineare.
.La regressione lineare è una tecnica statistica utilizzata per trovare la relazione tra variabili. In un modello ML di contesto, la regressione lineare individua la relazione tra features e a etichetta.
Ad esempio, supponiamo di voler prevedere il consumo di carburante di un'auto in miglia per galloni in base al peso dell'auto, e abbiamo il seguente set di dati:
| Libbre in migliaia (caratteristica) | Miglia per gallone (etichetta) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Se tracciassimo questi punti, otterremmo il seguente grafico:
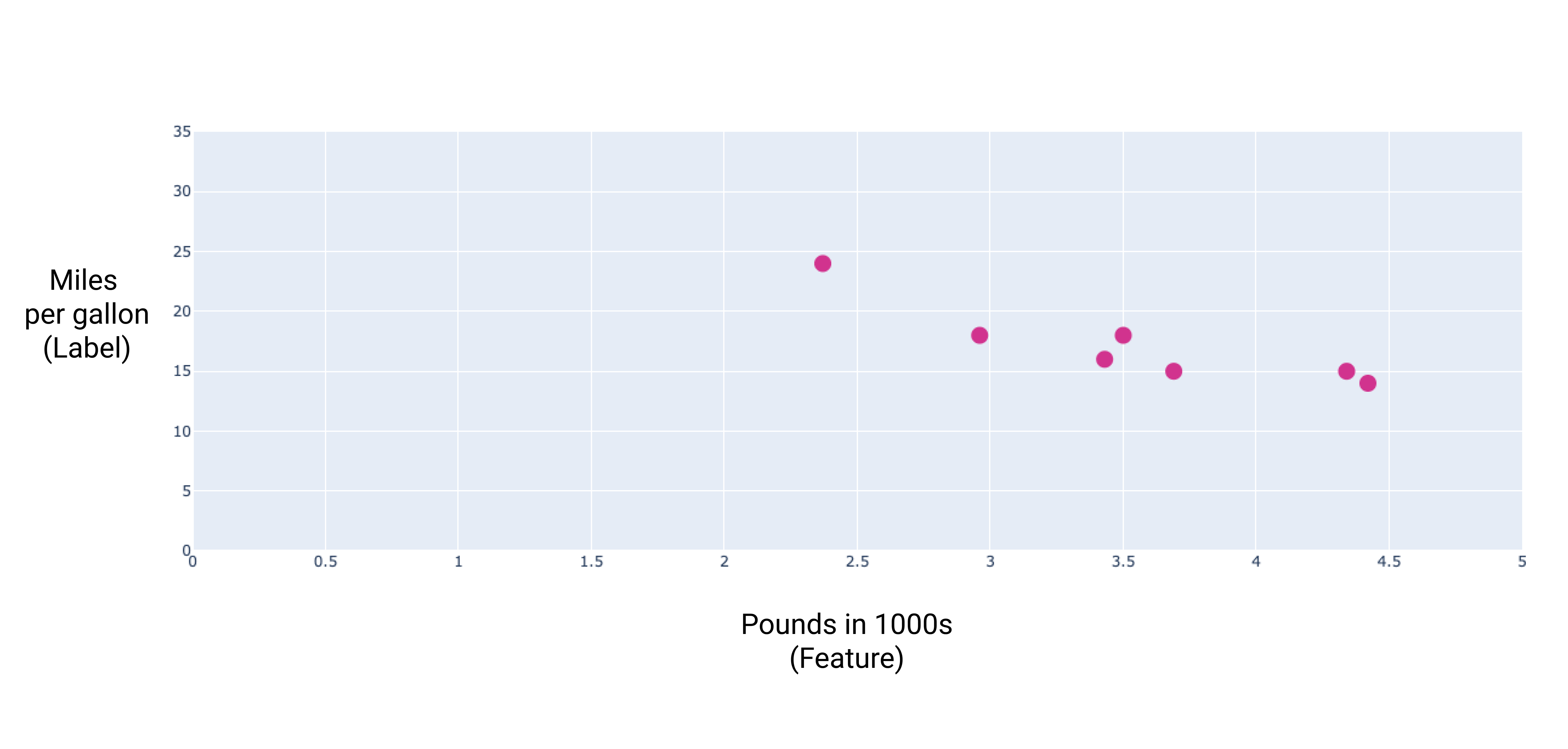
Figura 1. Spessore dell'auto (in libbre) rispetto alla valutazione delle miglia per gallone. Come un'auto diventa più pesante, il valore delle miglia per gallone generalmente diminuisce.
Potremmo creare il nostro modello disegnando una linea di adattamento migliore attraverso i punti:
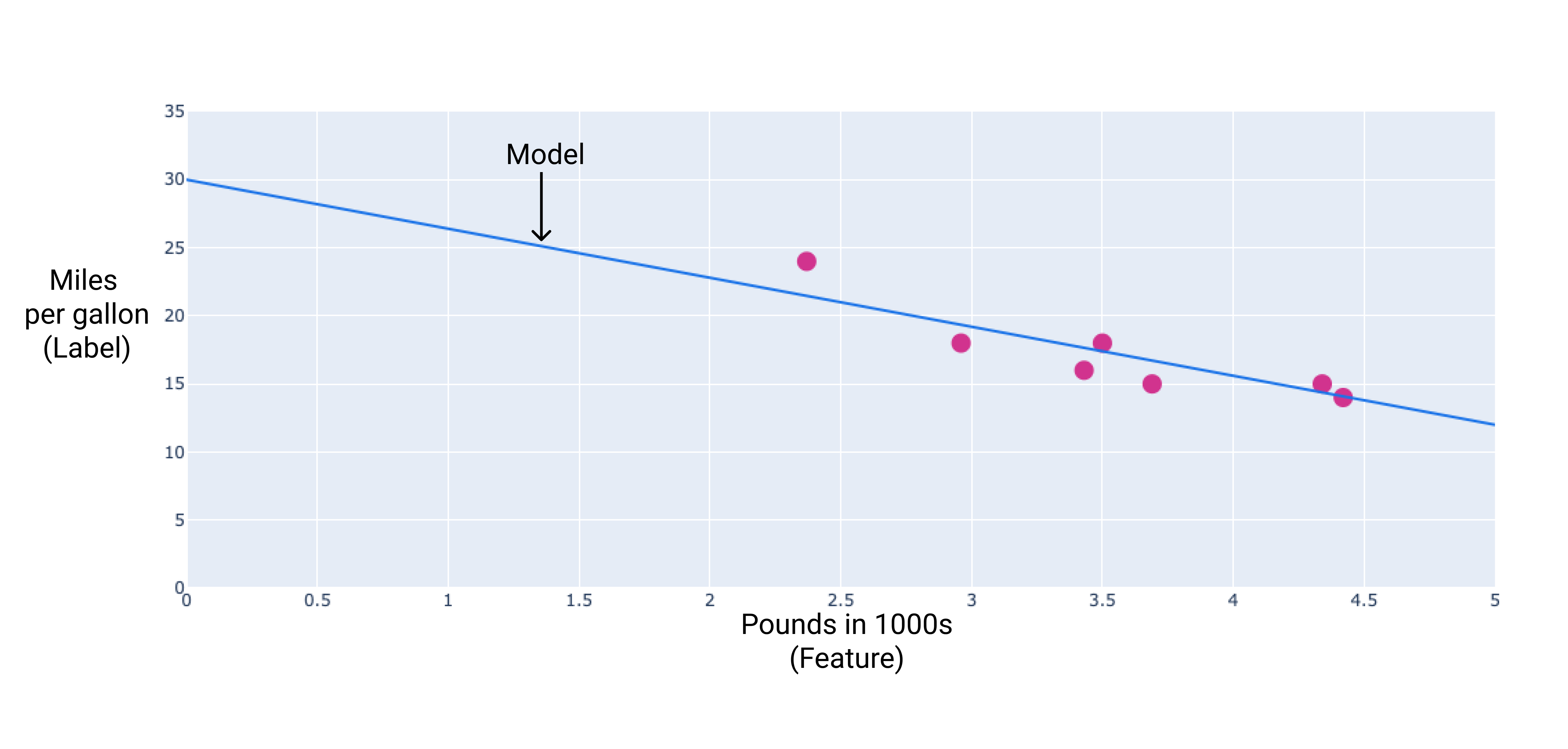
Figura 2. Una linea di adattamento ottimale tracciata attraverso i dati della figura precedente.
Equazione di regressione lineare
In termini algebrici, il modello sarebbe definito come $ y = mx + b $, dove
- $ y $ corrisponde a miglia per gallone, il valore che vogliamo prevedere.
- $ m $ è la pendenza della linea.
- $ x $ sono libbre, il nostro valore di input.
- $ b $ è l'intercetta sull'asse y.
In ML, scriviamo l'equazione per un modello di regressione lineare come segue:
dove:
- $ a $ è l'etichetta prevista, ovvero l'output.
- $ b $ è il pregiudizio del modello. Il bias è lo stesso concetto dell'intercetta y nell'ambito algebrico dell'equazione di una retta. Nel ML, a volte il bias viene chiamato w_0 $. Pregiudizi è un parametro del modello e viene calcolata durante l'addestramento.
- $ w_1 $ è il peso del funzionalità. Il peso è lo stesso concetto della pendenza $ m $ nel linguaggio algebrico dell'equazione di una retta. Il peso è un parameter del modello ed è calcolate durante l'addestramento.
- $ x_1 $ è una caratteristica, ovvero di testo.
Durante l'addestramento, il modello calcola la ponderazione e il bias che producono i risultati migliori un modello di machine learning.
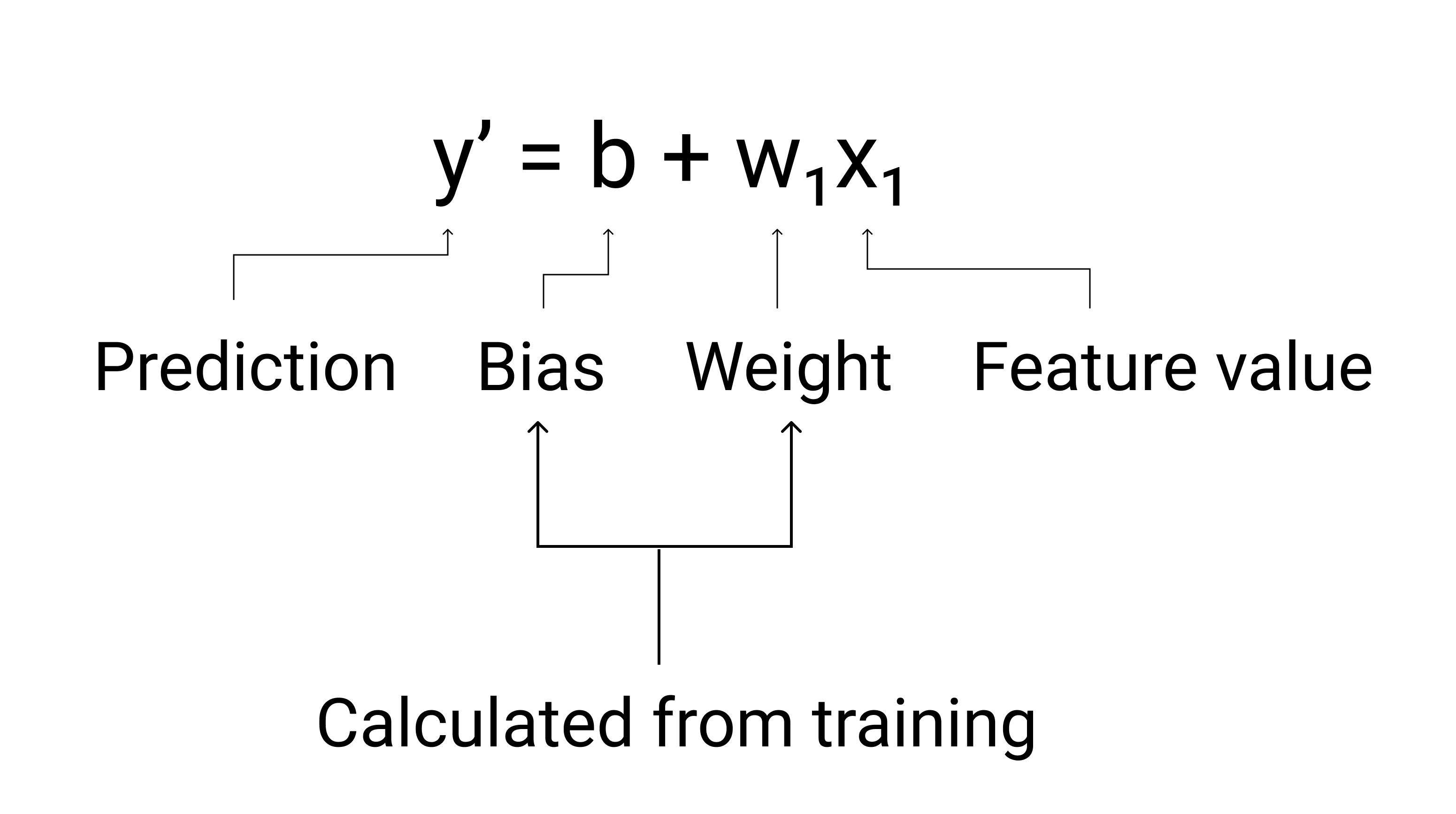
Figura 3. Rappresentazione matematica di un modello lineare.
Nel nostro esempio, abbiamo calcolato la ponderazione e il bias dalla linea tracciata. La bias è 30 (dove la linea interseca l'asse y) e la ponderazione è -3,6 (la pendenza della linea). Il modello viene definito come y $. = 30 + (-3, 6)(x_1) $ e potremmo utilizzarlo per fare previsioni. Ad esempio, utilizzando questo modello, Un'auto da 4.000 libbre avrebbe un'efficienza di carburante prevista di 25,6 miglia per galloni.
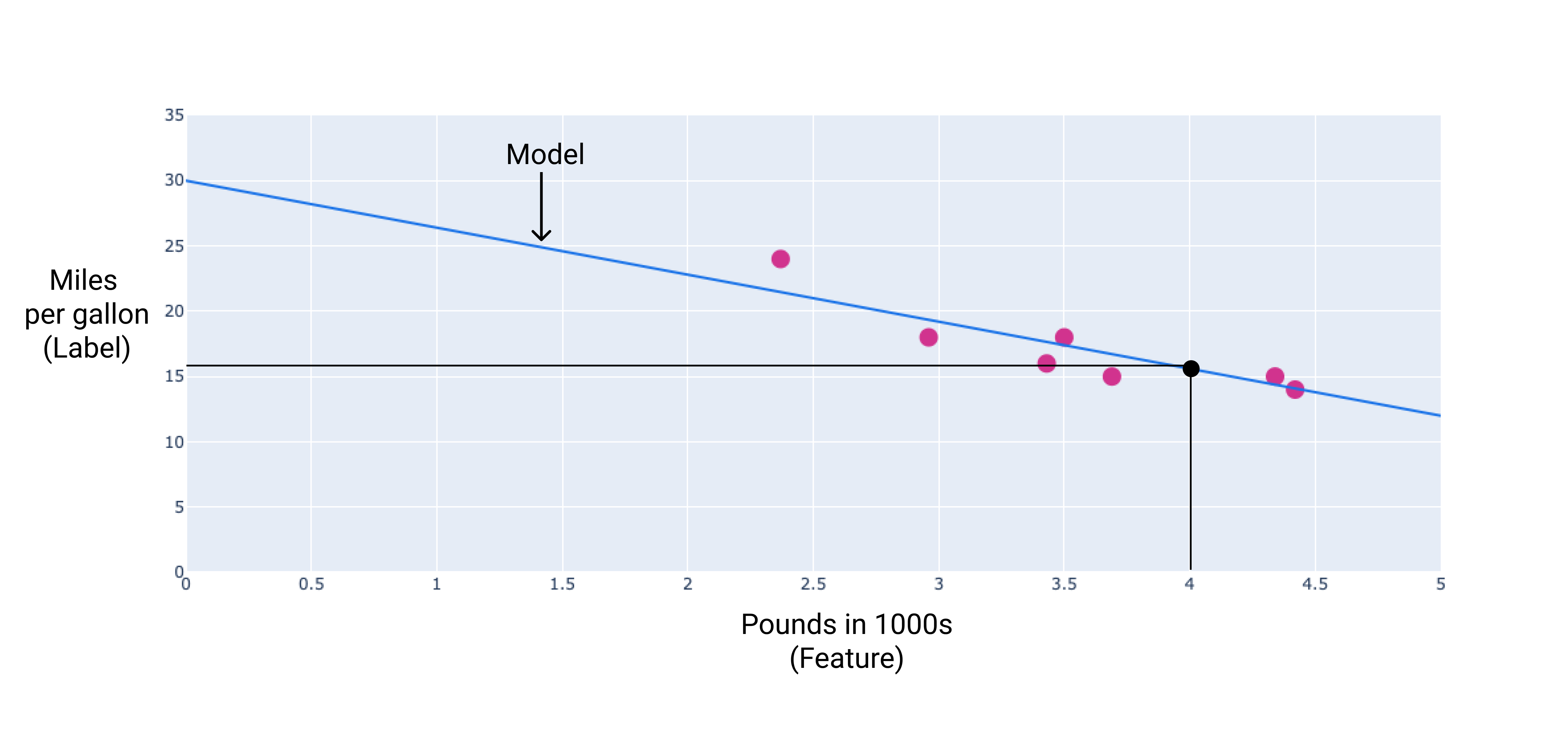
Figura 4. Utilizzando il modello, un'auto da 1700 kg ha una il consumo di carburante è di 25,6 miglia per gallone.
Modelli con più caratteristiche
Sebbene l'esempio in questa sezione utilizzi solo una caratteristica: la dell'auto: un modello più sofisticato potrebbe basarsi su più funzionalità, ciascuna con un peso diverso ($ w_1 $, $ w_2 $ e così via). Ad esempio, un modello che si basa su cinque caratteristiche sarebbe scritto come segue:
$ a = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Ad esempio, un modello che prevede il consumo di carburante potrebbe utilizzare anche caratteristiche ad esempio:
- Cilindrata
- Accelerazione
- Numero di cilindri
- Cavallo vapore
Questo modello verrebbe scritto come segue:
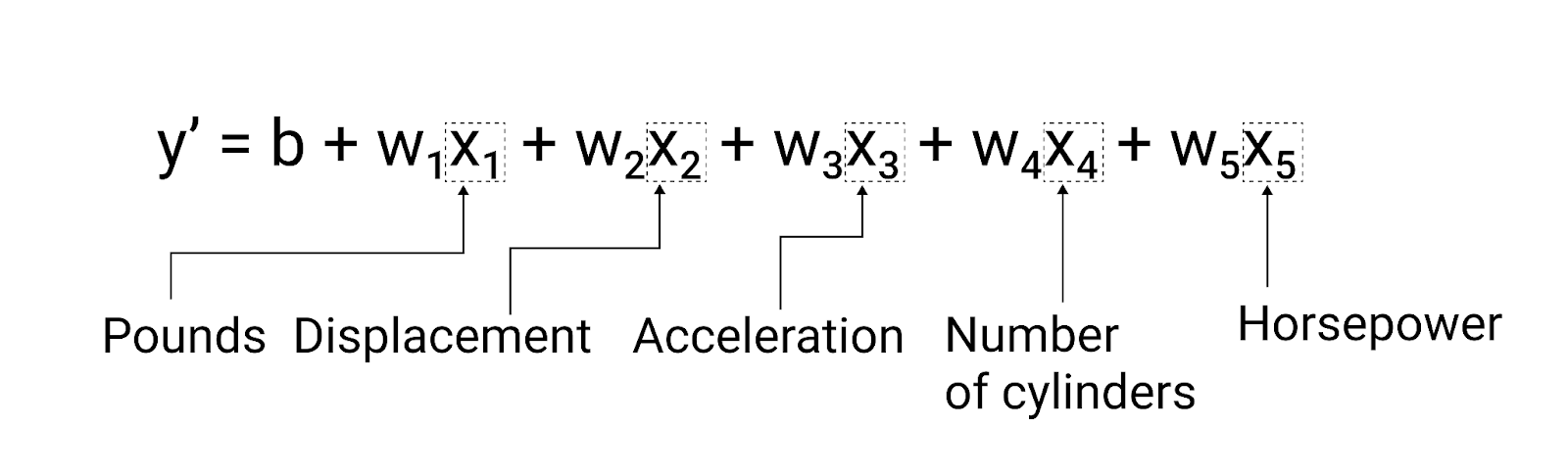
Figura 5. Un modello con cinque caratteristiche per prevedere le miglia per gallone di un'auto valutazione.
Rappresentando graficamente alcune di queste caratteristiche aggiuntive, possiamo vedere che hanno anche un relazione lineare con l'etichetta, miglia per gallone:
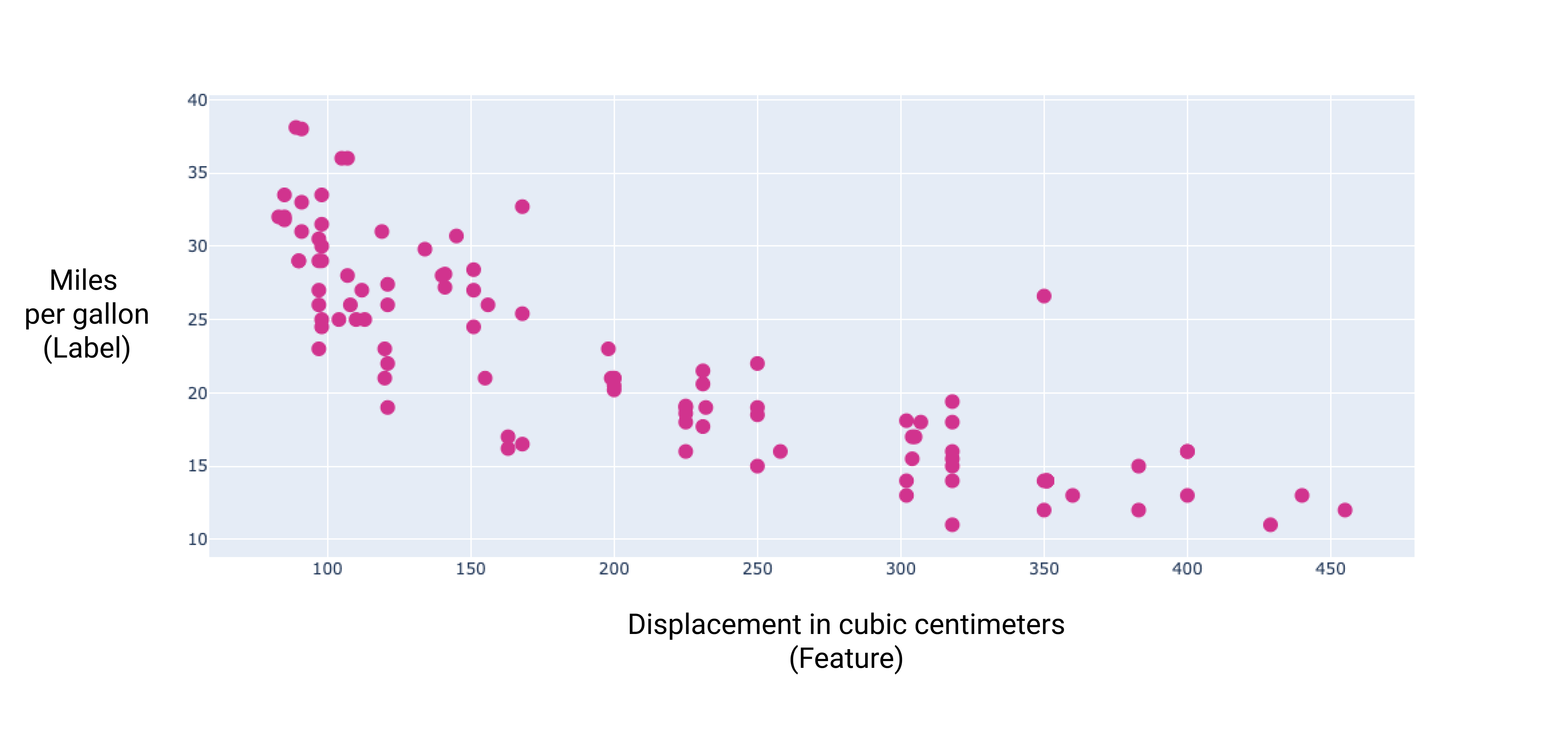
Figura 6. Lo spostamento di un'auto in centimetri cubi e le sue miglia per gallone valutazione. Quando il motore di un'auto diventa più grande, in genere il valore delle miglia per gallone diminuisce.
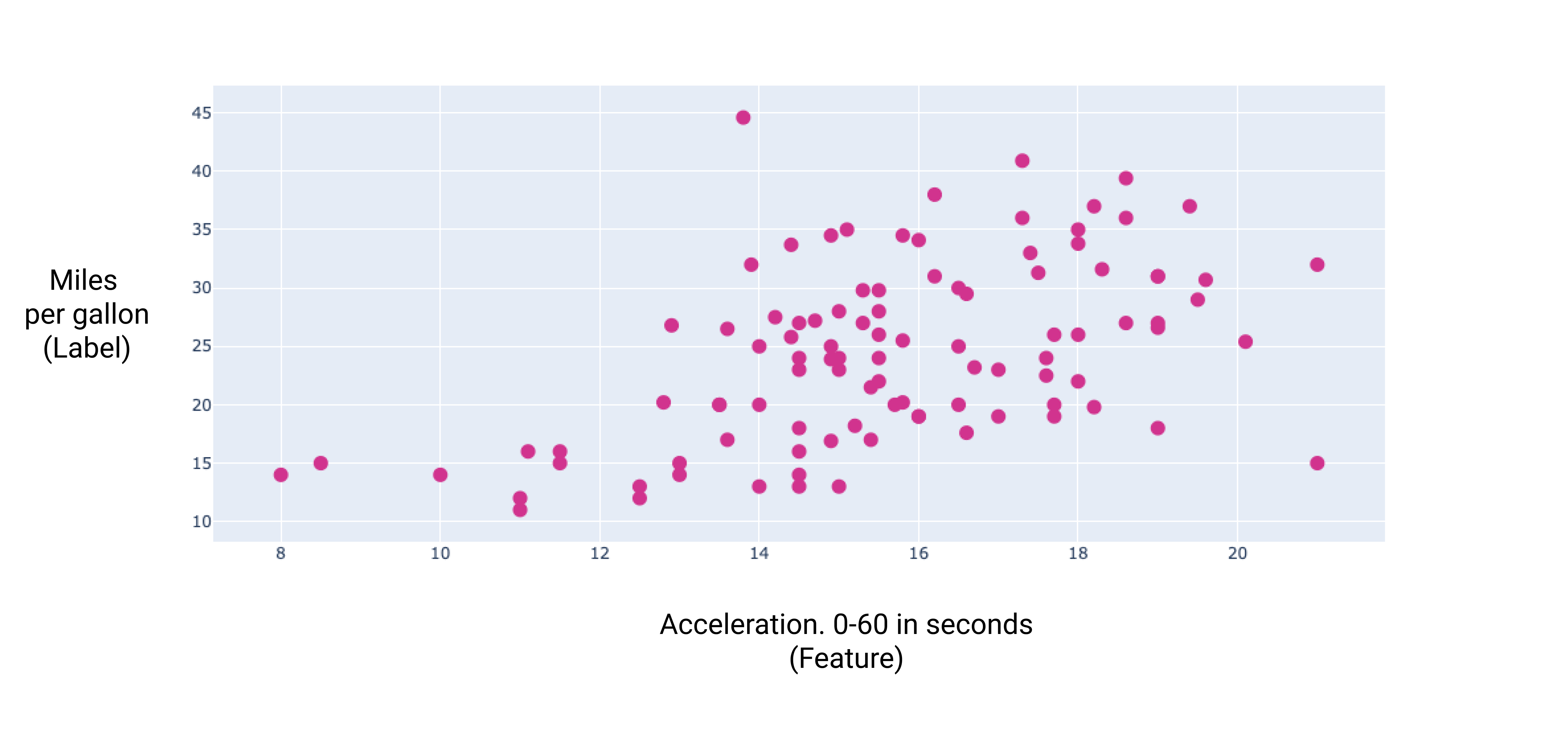
Figura 7. L'accelerazione di un'auto e le relative miglia per gallone. Come un'auto l'accelerazione richiede più tempo, il valore delle miglia per gallone generalmente aumenta.
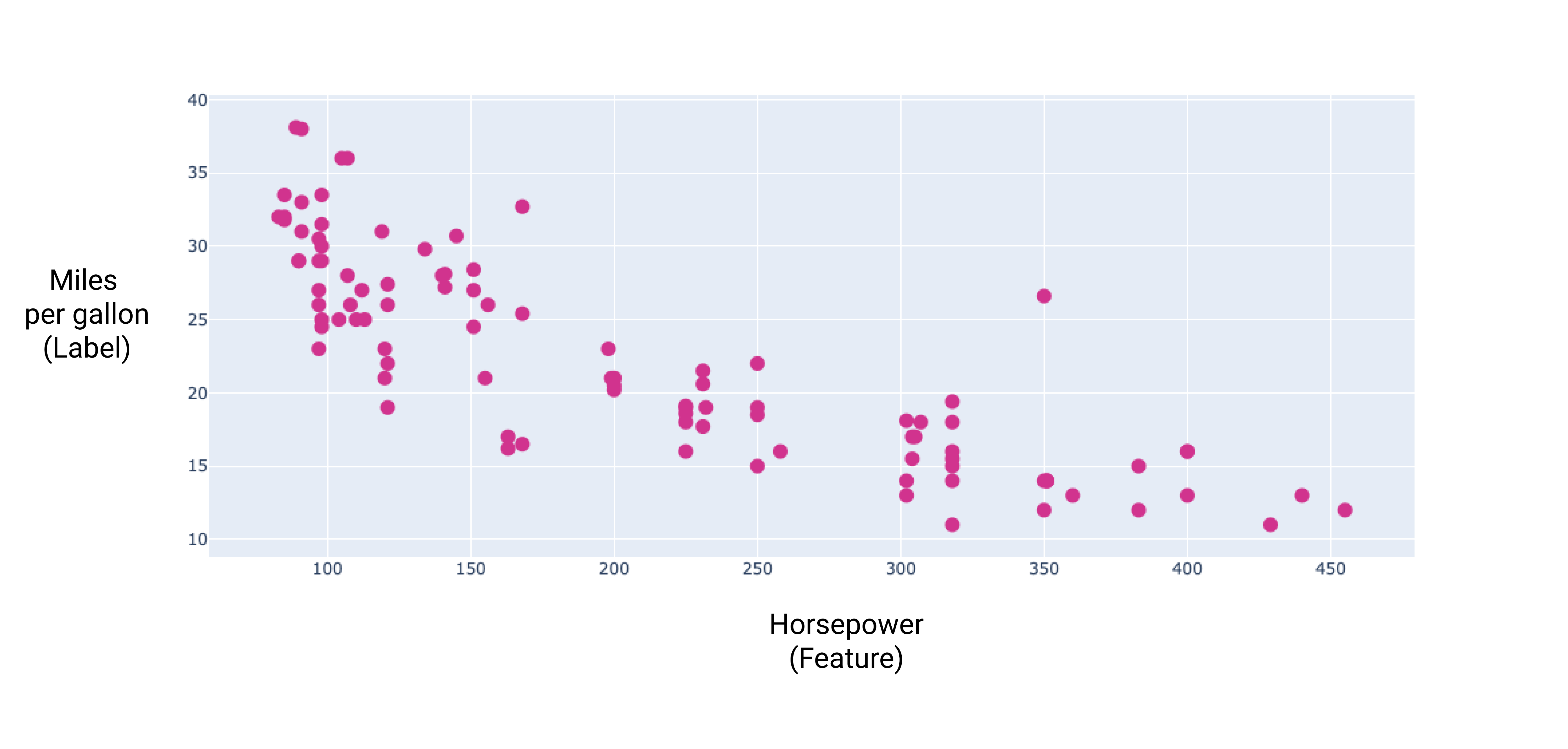
Figura 8. La potenza in cavalli di un'auto e le sue miglia per gallone. Come un'auto la potenza aumenta, le miglia per gallone generalmente diminuiscono.
