โมดูลนี้จะแนะนำแนวคิดการถดถอยเชิงเส้น
การถดถอยเชิงเส้นคือ เทคนิคทางสถิติที่ใช้เพื่อหาความสัมพันธ์ระหว่างตัวแปร ใน ML บริบท การถดถอยเชิงเส้นจะหาความสัมพันธ์ระหว่าง features และ label
ตัวอย่างเช่น สมมติว่าเราต้องการคาดการณ์การประหยัดเชื้อเพลิงของรถ หน่วยเป็นไมล์ต่อ แกลลอนโดยพิจารณาจากความหนักของรถ และเรามีชุดข้อมูลต่อไปนี้
| ปอนด์ใน 1,000 วินาที (ฟีเจอร์) | ไมล์ต่อแกลลอน (ป้ายกำกับ) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
หากเราพล็อตจุดเหล่านี้ เราจะได้กราฟต่อไปนี้
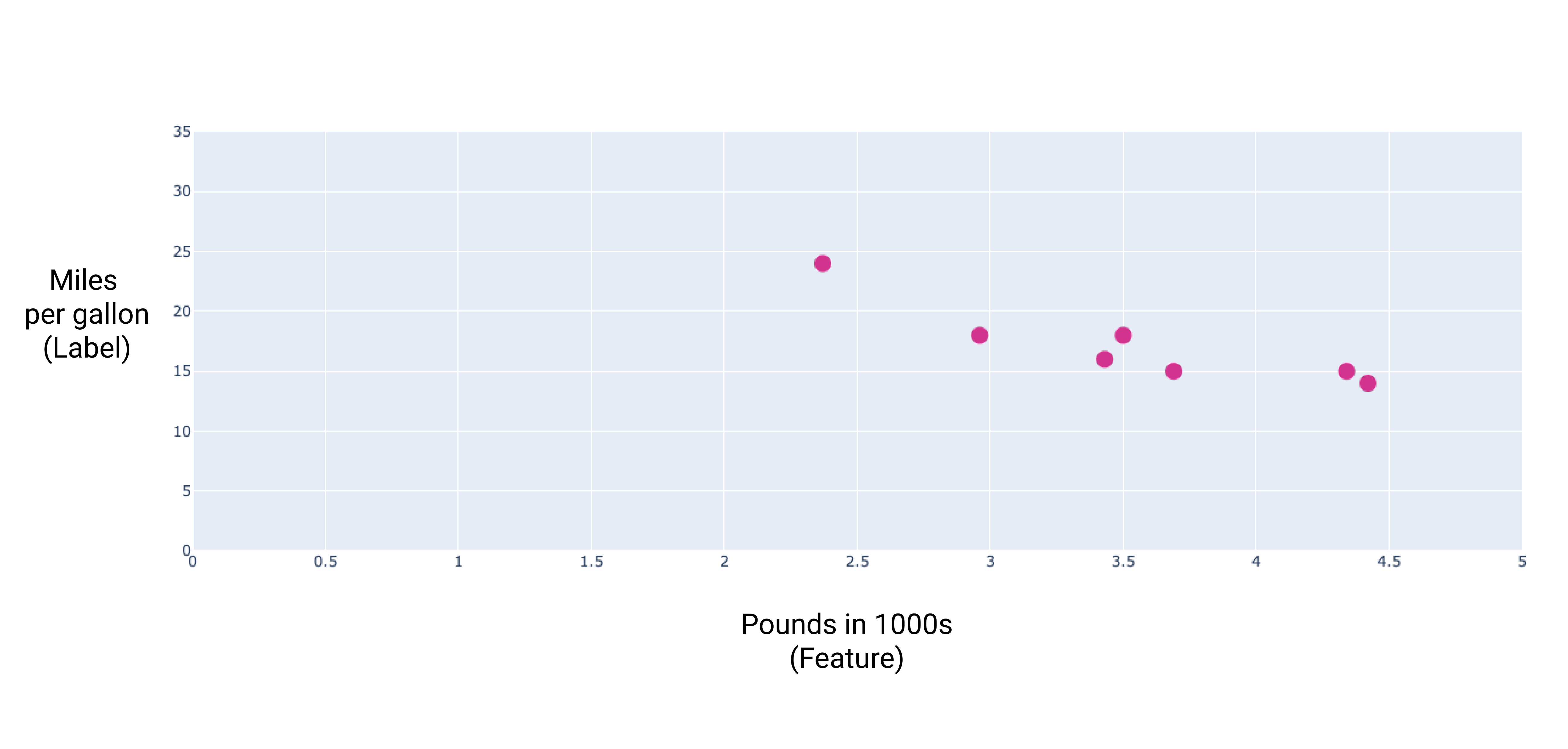
รูปที่ 1 ความหนักของรถ (เป็นปอนด์) เทียบกับไมล์ต่อแกลลอน เพื่อ รถมีน้ำหนักมากขึ้น คะแนนไมล์ต่อแกลลอนโดยทั่วไปจะลดลง
เราสามารถสร้างโมเดลของเราเองได้โดยการวาดเส้นที่พอดีที่สุดผ่านจุดต่างๆ:
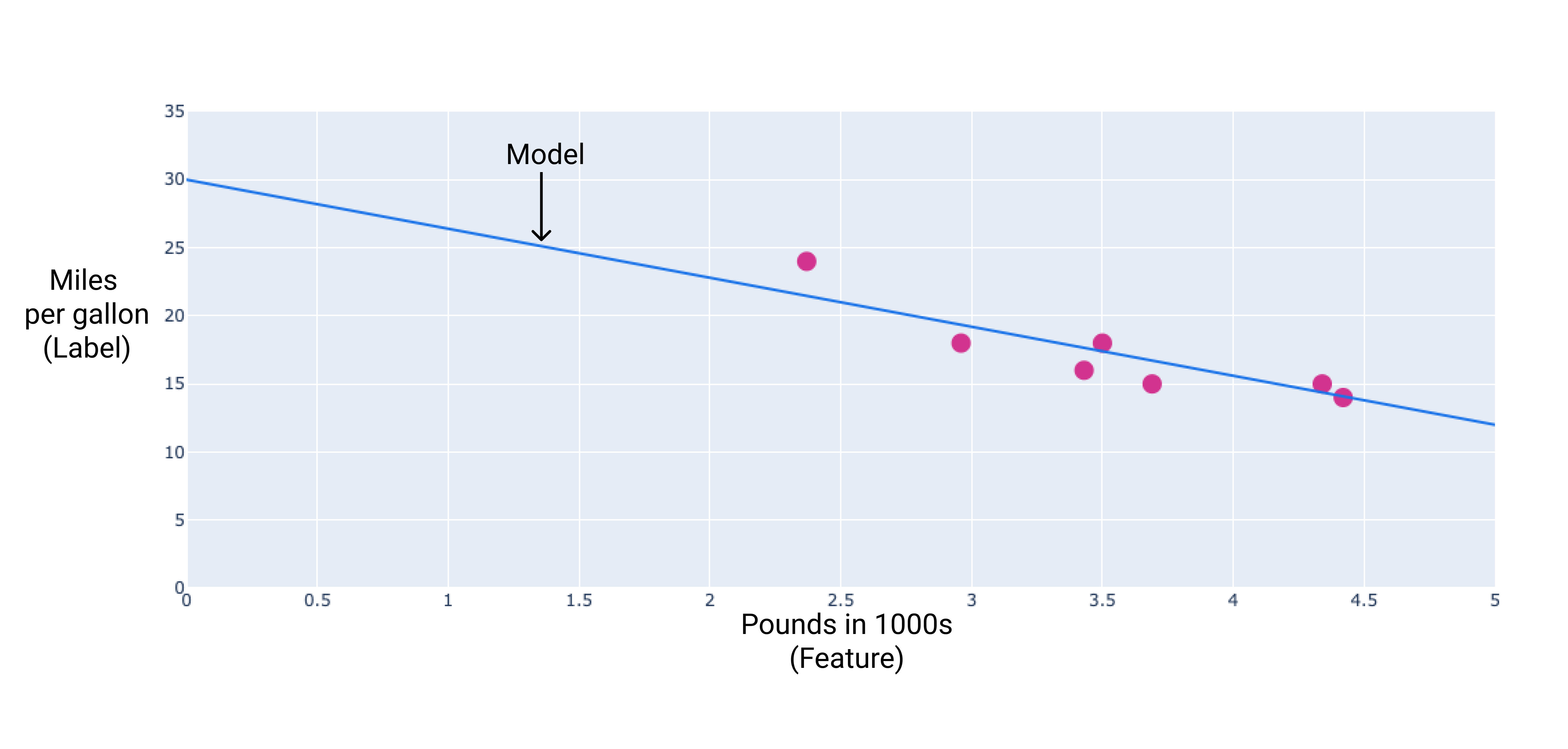
รูปที่ 2 เส้นที่พอดีที่สุดวาดผ่านข้อมูลจากรูปก่อนหน้า
สมการการถดถอยเชิงเส้น
ในศัพท์พีชคณิต โมเดลจะถือเป็น $ y = mx + b $ โดยที่
- $ y $ คือไมล์ต่อแกลลอน ซึ่งเป็นค่าที่เราต้องการคาดการณ์
- $ m $ คือความชันของเส้น
- $ x $ คือปอนด์ ซึ่งก็คือค่าอินพุตของเรา
- $ b $ คือจุดตัด y
ใน ML เราเขียนสมการสำหรับโมเดลการถดถอยเชิงเส้นดังต่อไปนี้
โดยมี
- $ y' $ คือป้ายกำกับที่คาดการณ์ ซึ่งเป็นเอาต์พุต
- $ b $ คืออคติ ของโมเดลดังกล่าว การให้น้ำหนักพิเศษเป็นแนวคิดเดียวกับจุดตัด y ในพีชคณิต สมการของเส้นตรง ใน ML บางครั้งจะเรียกว่า $ w_0 $ การให้น้ำหนักพิเศษ เป็นพารามิเตอร์ของโมเดลและ ซึ่งคำนวณระหว่างการฝึก
- $ w_1 $ คือน้ำหนักของ น้ำหนักมีแนวคิดเดียวกับความชัน $ m $ ในพีชคณิต สมการของเส้นตรง น้ำหนักคือ parameter ของโมเดลและ โดยคำนวณระหว่างการฝึก
- $ x_1 $ คือฟีเจอร์ อินพุต
ในระหว่างการฝึกฝน โมเดลจะคำนวณน้ำหนักและความลำเอียงที่ให้ผลลัพธ์ที่ดีที่สุด โมเดล
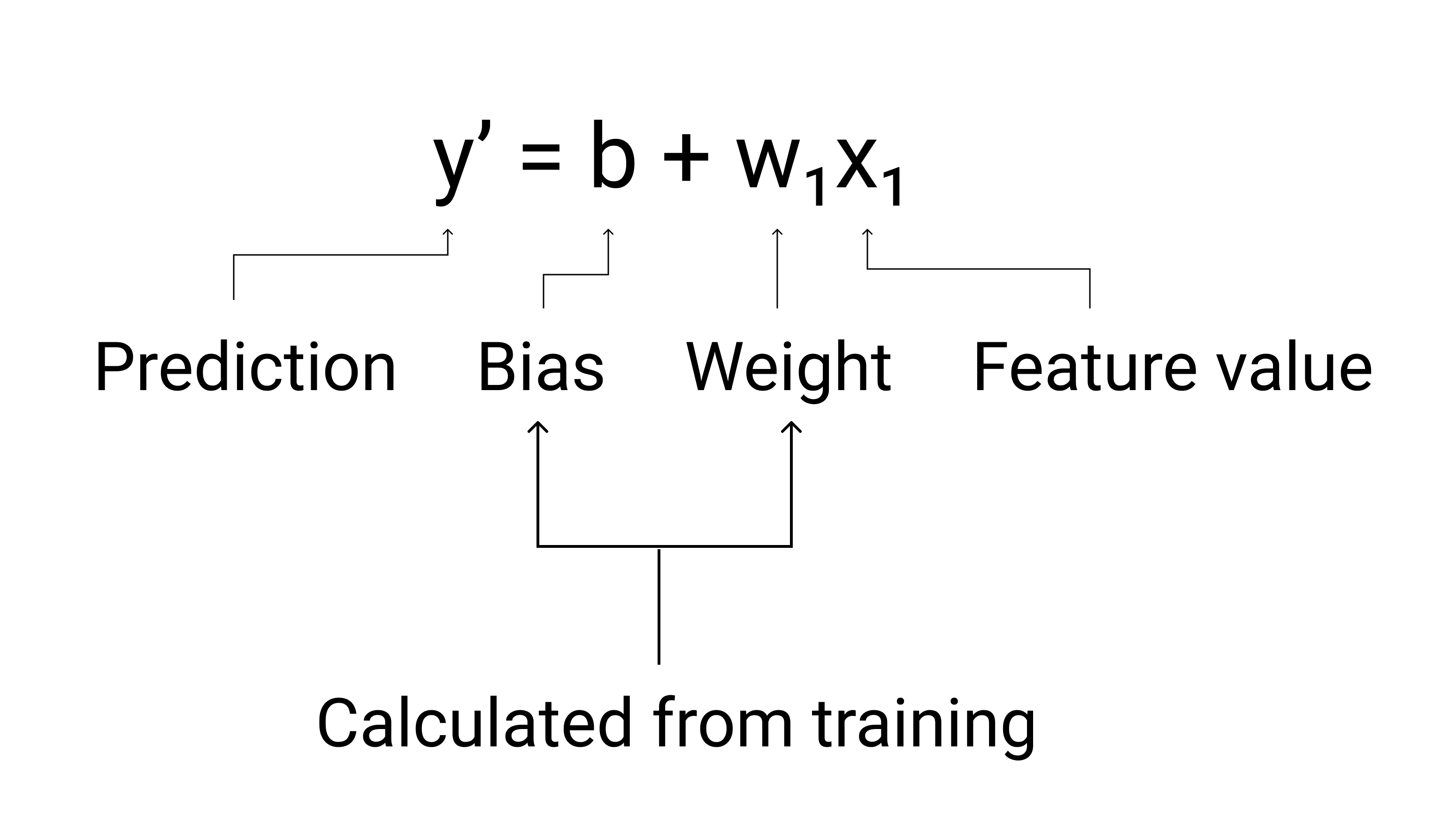
รูปที่ 3 การนำเสนอทางคณิตศาสตร์ของโมเดลเชิงเส้น
ในตัวอย่างของเรา เราจะคำนวณน้ำหนักและความเอนเอียงจากเส้นที่วาด ค่าลำเอียงคือ 30 (โดยที่เส้นตัดกับแกน y) และน้ำหนักคือ -3.6 (ค่า ความลาดชันของเส้น) โมเดลจะได้รับการกำหนดเป็น $ y' = 30 + (-3.6)(x_1) $ และ เราสามารถนำมาใช้ในการคาดการณ์ ตัวอย่างเช่น การใช้โมเดลนี้ รถขนาด 4,000 ปอนด์น่าจะประหยัดเชื้อเพลิงได้ถึง 15.6 ไมล์ต่อ แกลลอน
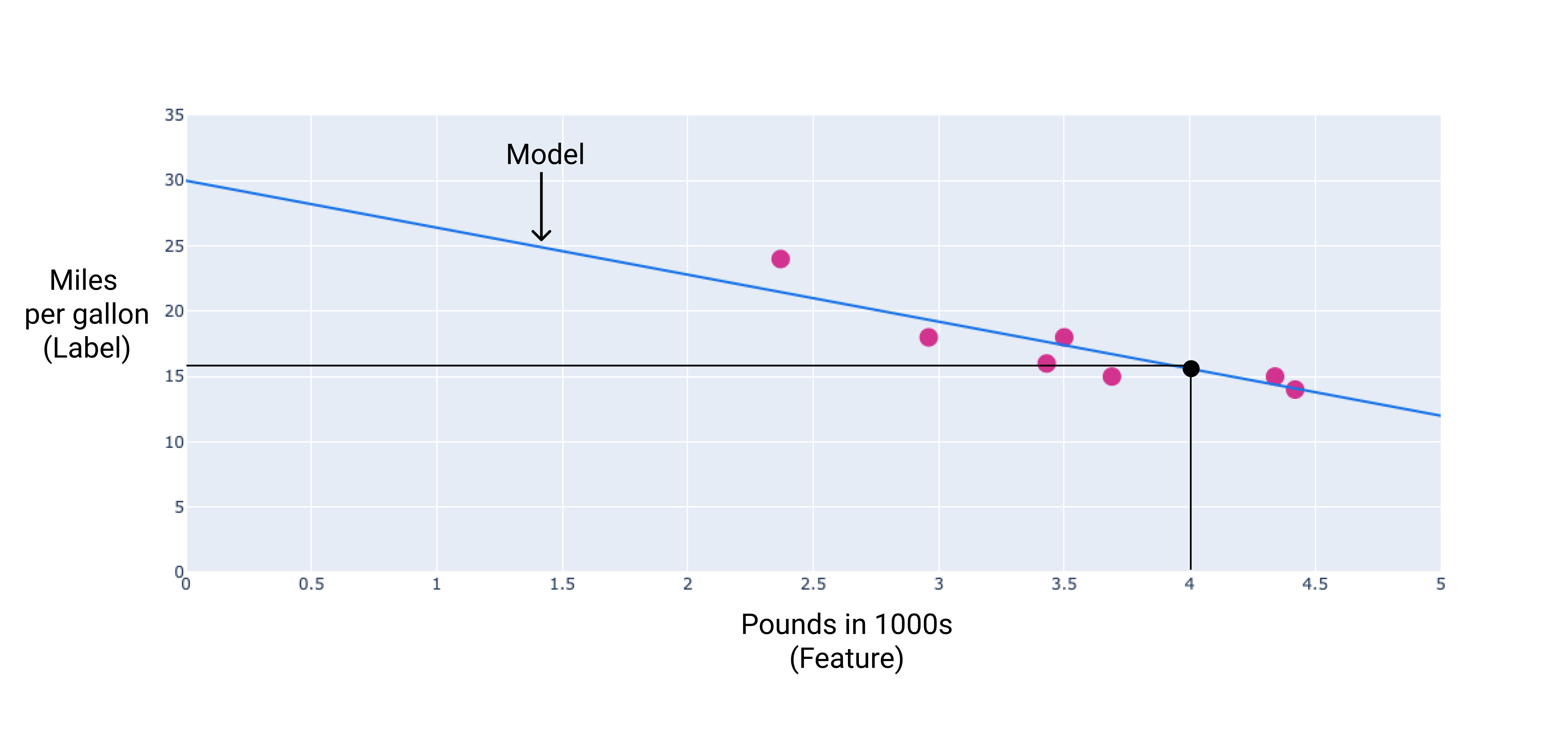
รูปที่ 4 เมื่อใช้โมเดลนี้ รถที่มีน้ำหนัก 4,000 ปอนด์จะมีการคาดการณ์ว่า ประหยัดเชื้อเพลิง 15.6 ไมล์ต่อแกลลอน
โมเดลที่มีหลายฟีเจอร์
แม้ว่าตัวอย่างในส่วนนี้จะใช้เพียงฟีเจอร์เดียว นั่นก็คือความหนา ของรถยนต์ โมเดลที่ซับซ้อนขึ้นอาจต้องใช้คุณลักษณะหลายอย่าง แต่ละรายการมีน้ำหนักแยกกัน ($ w_1 $, $ w_2 $ เป็นต้น) เช่น โมเดล ที่ต้องอาศัยคุณลักษณะ 5 ประการโดยแบ่งออกเป็นดังนี้
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
เช่น โมเดลที่คาดการณ์ว่าระยะประหยัดน้ำมันสามารถใช้ฟีเจอร์เพิ่มเติมได้ เช่น
- การกระจัดของเครื่องยนต์
- การเร่งความเร็ว
- จำนวนกระบอกสูบ
- แรงม้า
โมเดลนี้จะเขียนดังนี้
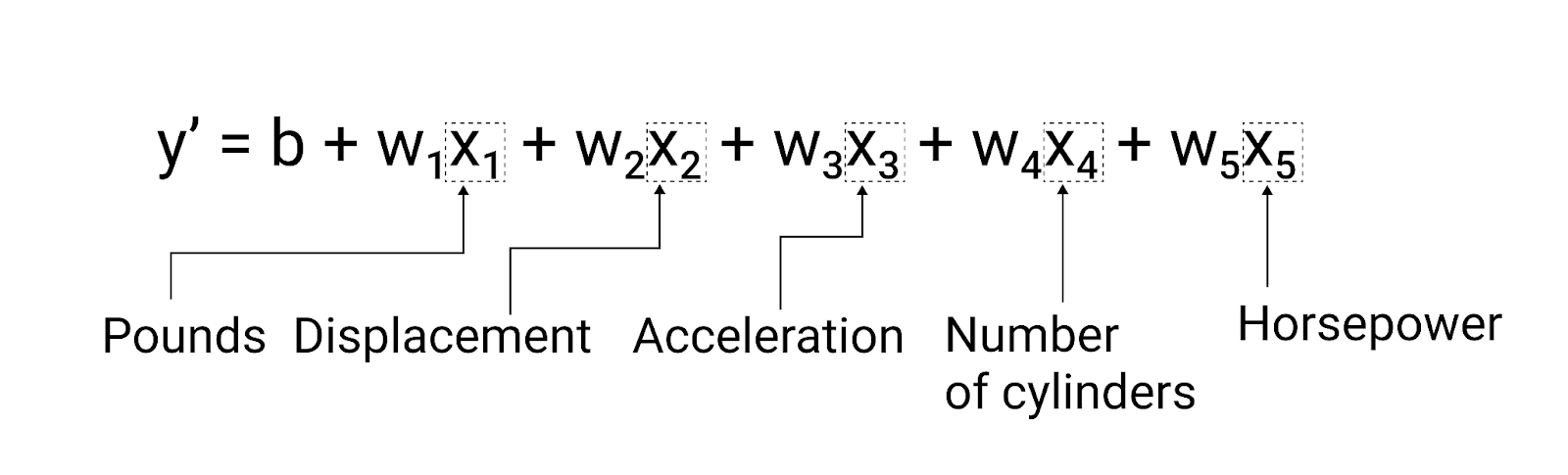
รูปที่ 5 แบบจำลองที่มีคุณลักษณะ 5 อย่างสำหรับทำนายระยะทางต่อแกลลอนของรถ คะแนน
การแสดงกราฟของคุณลักษณะเพิ่มเติมเหล่านี้บางส่วน ทำให้เราเห็นว่าคุณลักษณะเหล่านี้ยังมี ความสัมพันธ์เชิงเส้นกับป้ายกำกับ ไมล์ต่อแกลลอน:
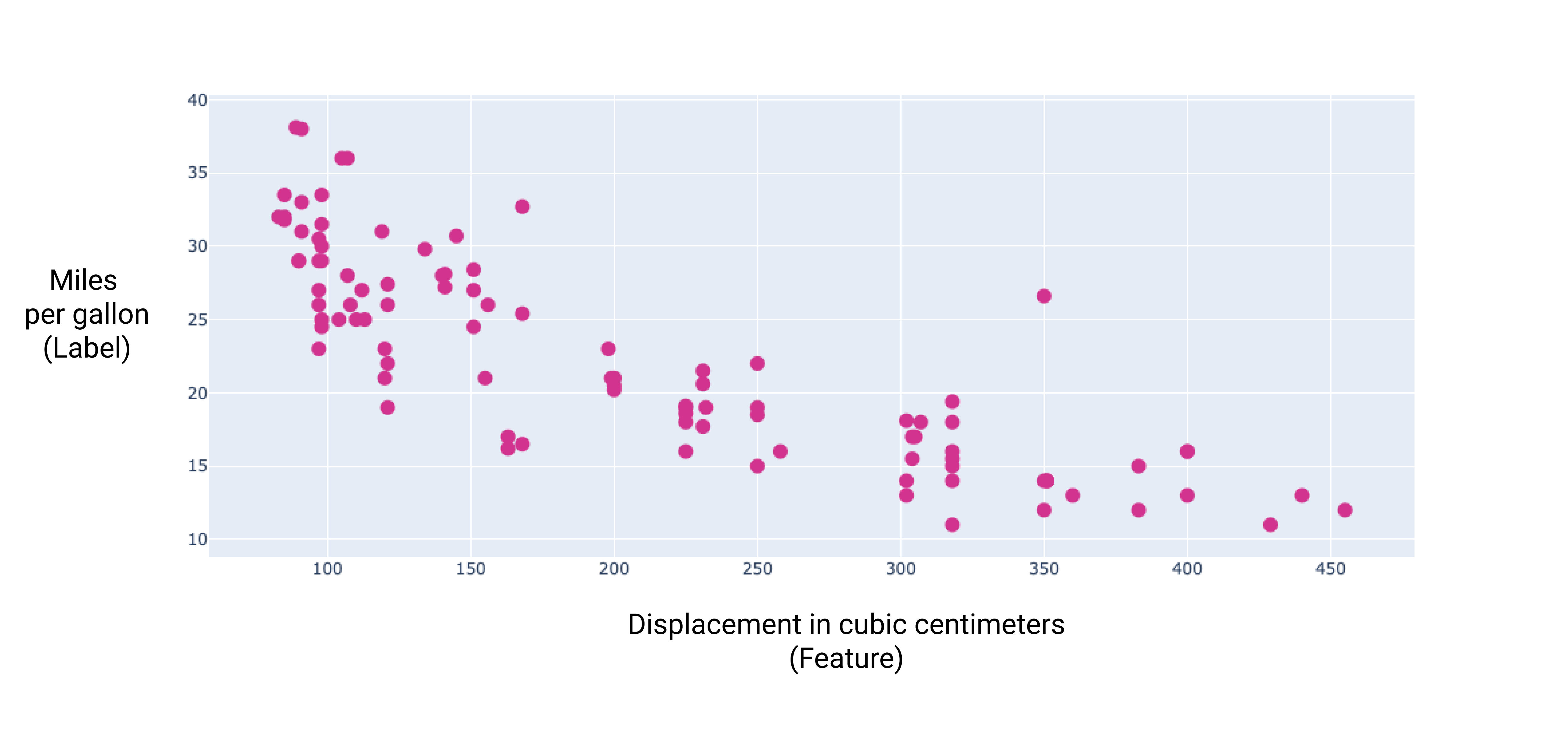
รูปที่ 6 ปริมาณการกระจัดของรถเป็นลูกบาศก์เซนติเมตรและไมล์ต่อแกลลอน คะแนน เมื่อเครื่องยนต์ของรถใหญ่ขึ้น โดยทั่วไปแล้วไมล์ต่อแกลลอน ลดลง
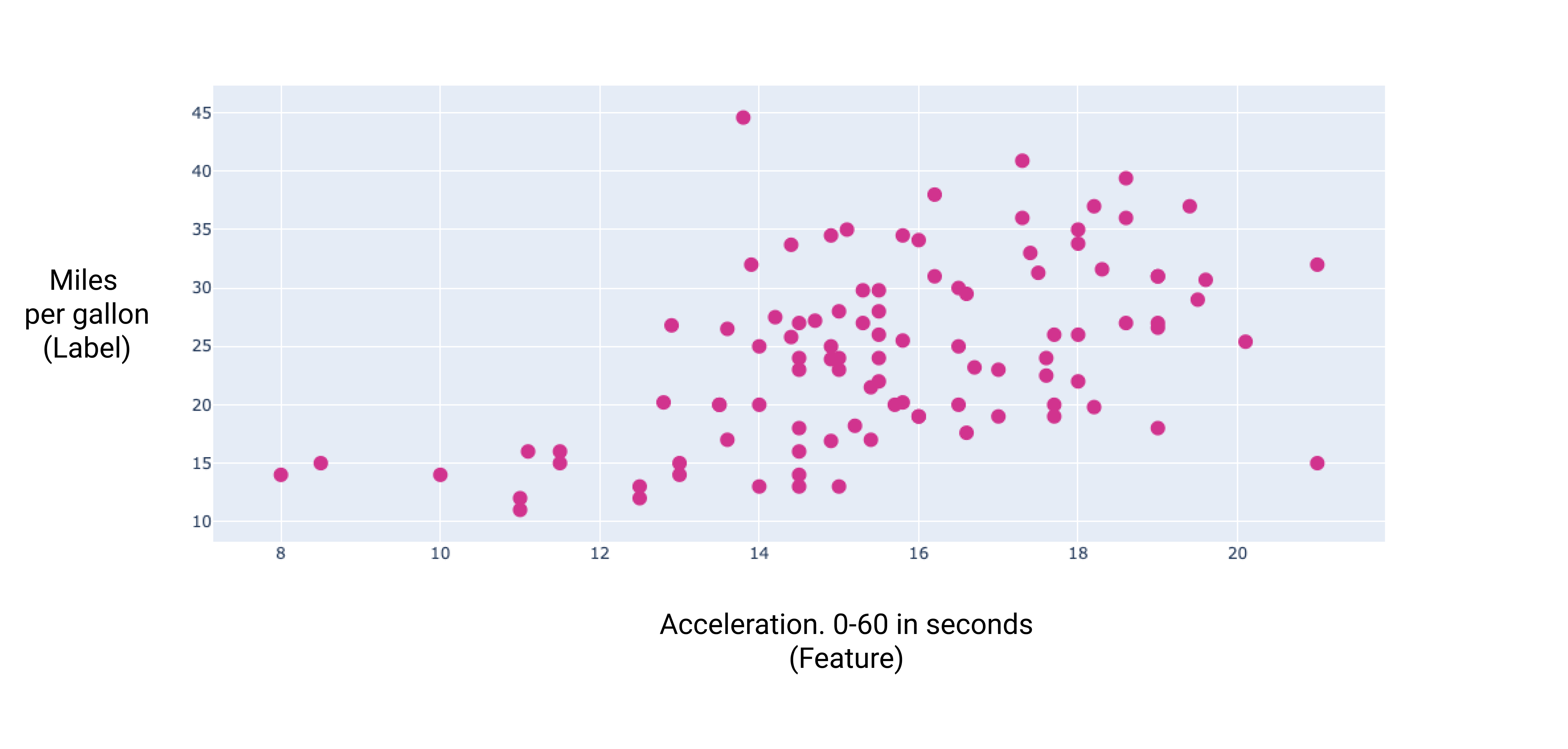
รูปที่ 7 ความเร่งของรถและไมล์ต่อแกลลอน ในฐานะรถยนต์ การเร่งความเร็วใช้เวลานานกว่าปกติ โดยทั่วไปแล้วคะแนนไมล์ต่อแกลลอนจะเพิ่มขึ้น
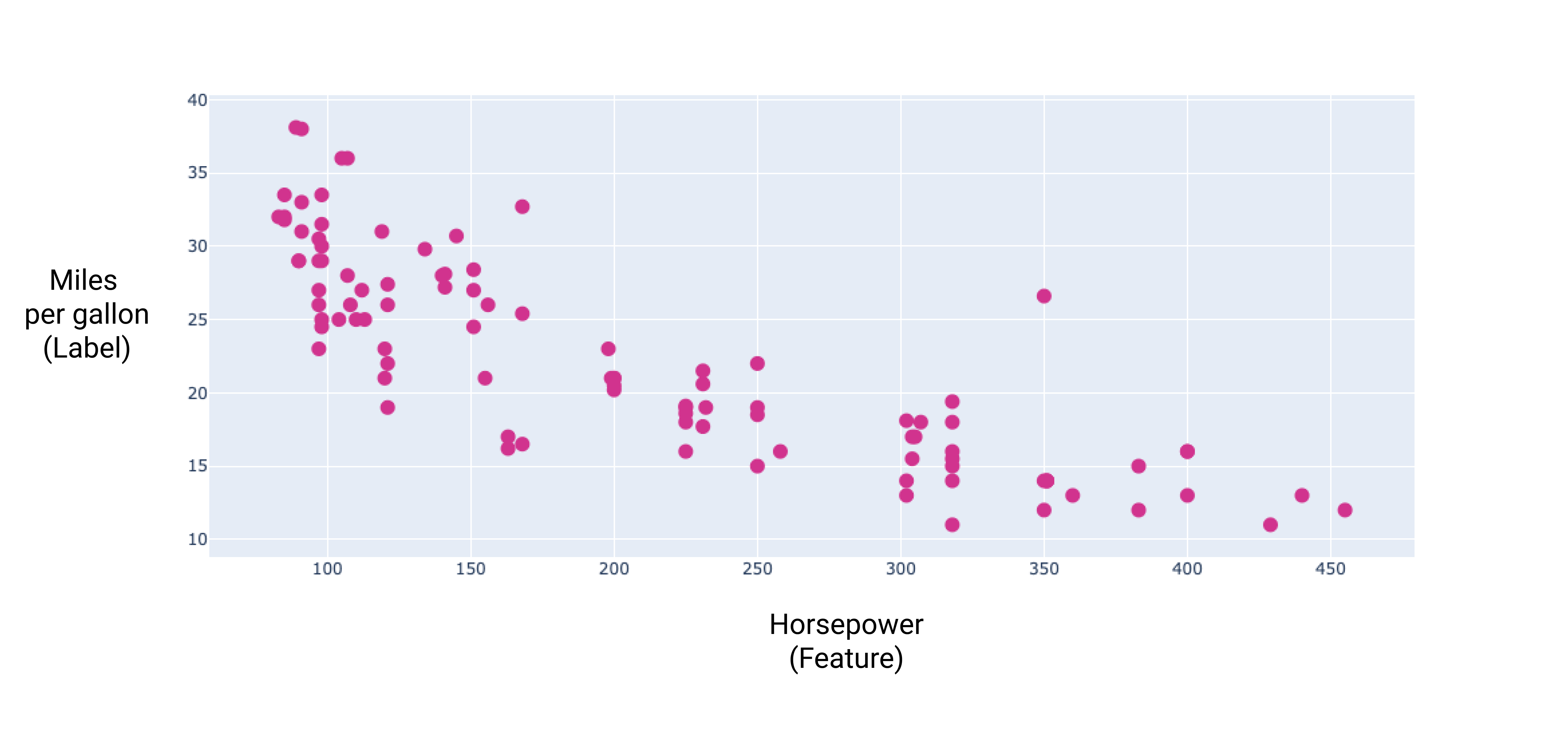
รูปที่ 8 แรงม้าของรถและไมล์ต่อแกลลอน ในฐานะรถยนต์ แรงม้าเพิ่มขึ้น แต่โดยทั่วไปแล้วคะแนนไมล์ต่อแกลลอนจะลดลง
