Ce module présente les concepts de régression linéaire.
La régression linéaire est une technique statistique utilisée pour trouver la relation entre les variables. Dans un contexte de ML, la régression linéaire trouve la relation entre les caractéristiques et un libellé.
Par exemple, supposons que nous voulions prédire la consommation de carburant d'une voiture en miles par gallon en fonction de son poids, et que nous disposions de l'ensemble de données suivant :
| Livres (en milliers) (fonctionnalité) | Milles par gallon (libellé) |
|---|---|
| 3.5 | 18 |
| 3,69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Si nous représentons ces points, nous obtenons le graphique suivant :
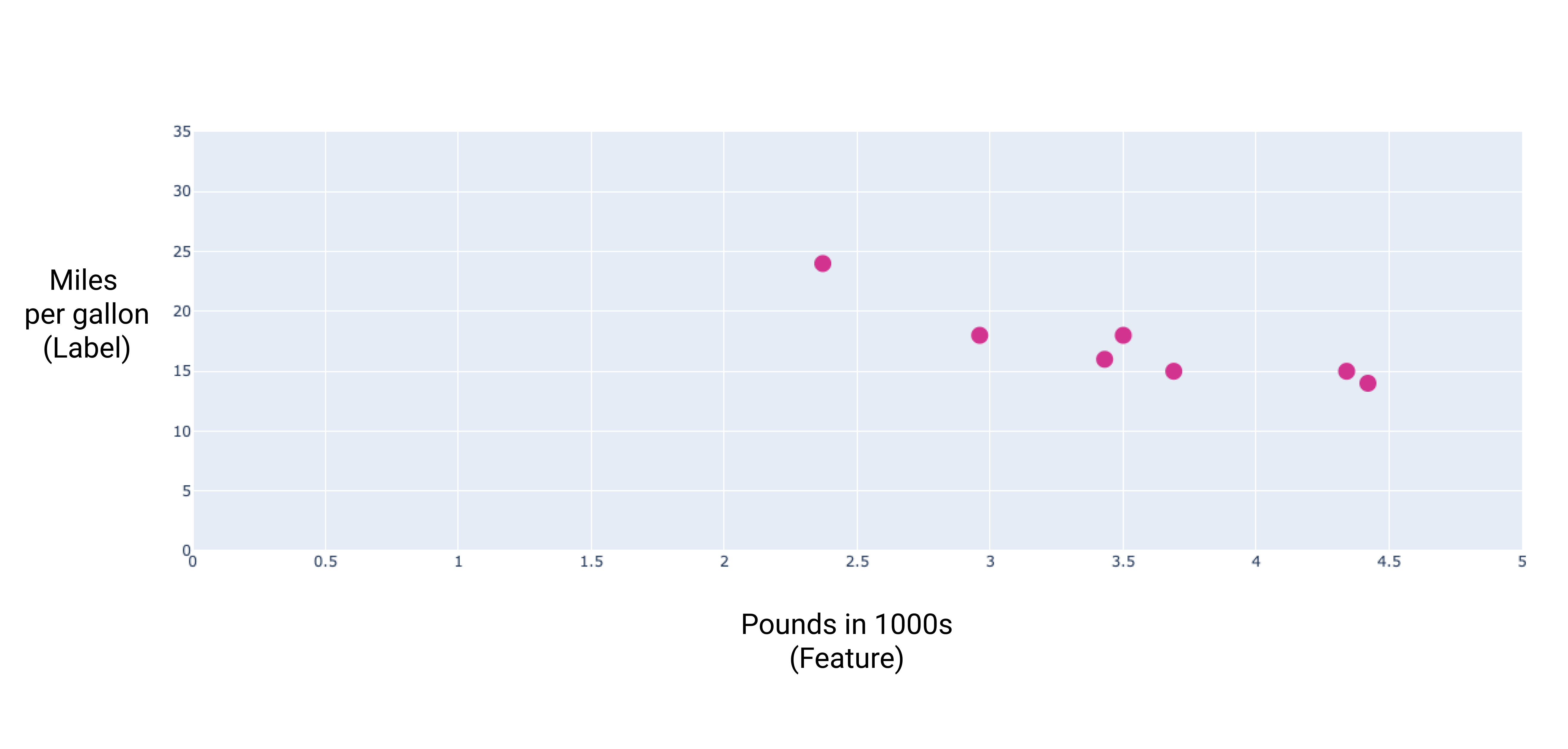
Figure 1 : Poids d'une voiture (en livres) par rapport à sa consommation de carburant en miles par gallon. Plus une voiture est lourde, plus sa consommation de carburant est élevée.
Nous pouvons créer notre propre modèle en traçant une ligne de régression à travers les points :
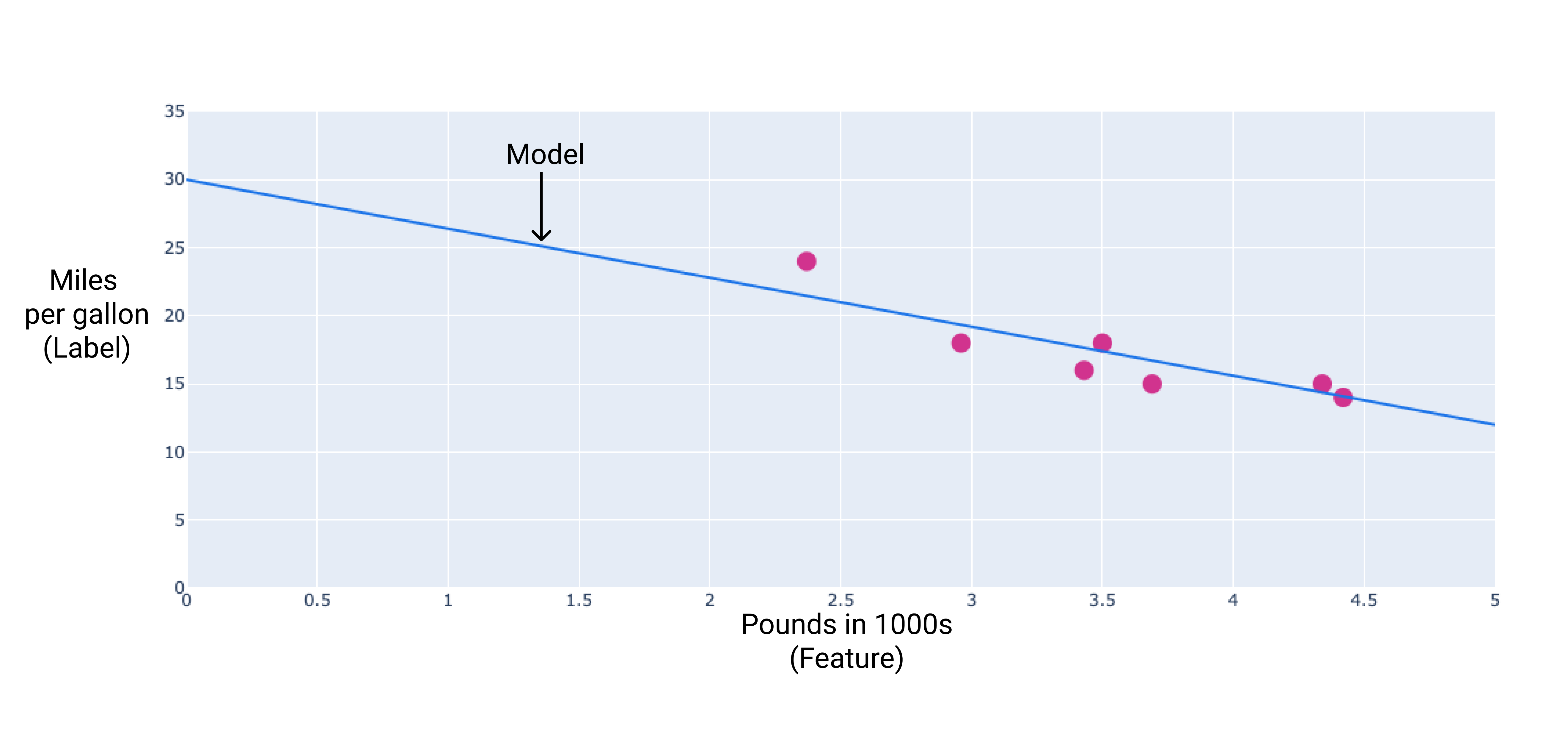
Figure 2 : Droite de régression tracée à travers les données de la figure précédente.
Équation de régression linéaire
En termes algébriques, le modèle serait défini comme $ y = mx + b $, où
- $ y $ correspond aux kilomètres par litre, soit la valeur que nous voulons prédire.
- $ m $ est la pente de la droite.
- \(x\) est le poids en livres, c'est-à-dire notre valeur d'entrée.
- $ b $ est l'ordonnée à l'origine.
En ML, l'équation d'un modèle de régression linéaire s'écrit comme suit :
où :
- $ y' $ est le libellé prédit (la sortie).
- $ b $ est le biais du modèle. Le biais est le même concept que l'ordonnée à l'origine dans l'équation algébrique d'une droite. En ML, le biais est parfois appelé $ w_0 $. Il s'agit d'un paramètre du modèle qui est calculé lors de l'entraînement.
- $ w_1 $ est le poids de la fonctionnalité. La pondération est un concept identique à celui de la pente $ m $ dans l'équation algébrique d'une droite. La pondération est un paramètre du modèle et est calculée lors de l'entraînement.
- $ x_1 $ est une caractéristique, c'est-à-dire l'entrée.
Lors de l'entraînement, le modèle calcule le poids et le biais qui produisent le meilleur modèle.
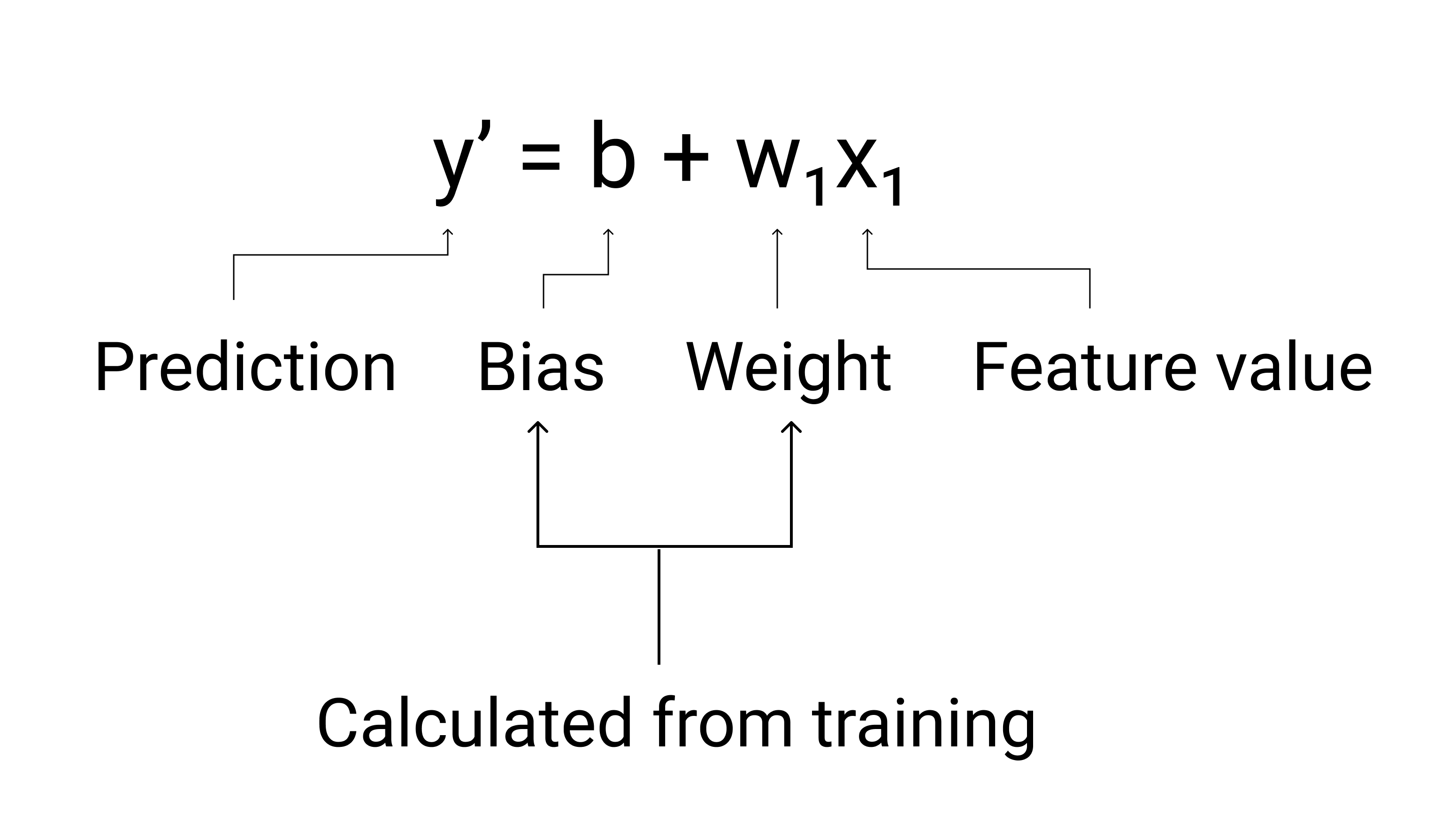
Figure 3. Représentation mathématique d'un modèle linéaire.
Dans notre exemple, nous calculerons le poids et le biais à partir de la ligne que nous avons tracée. Le biais est de 34 (où la ligne croise l'axe y) et le poids est de -4,6 (la pente de la ligne). Le modèle serait défini comme suit : $ y' = 34 + (-4.6)(x_1) $, et nous pourrions l'utiliser pour faire des prédictions. Par exemple, avec ce modèle, une voiture de 1 814 kg aurait une efficacité énergétique prévue de 6,6 km/l.
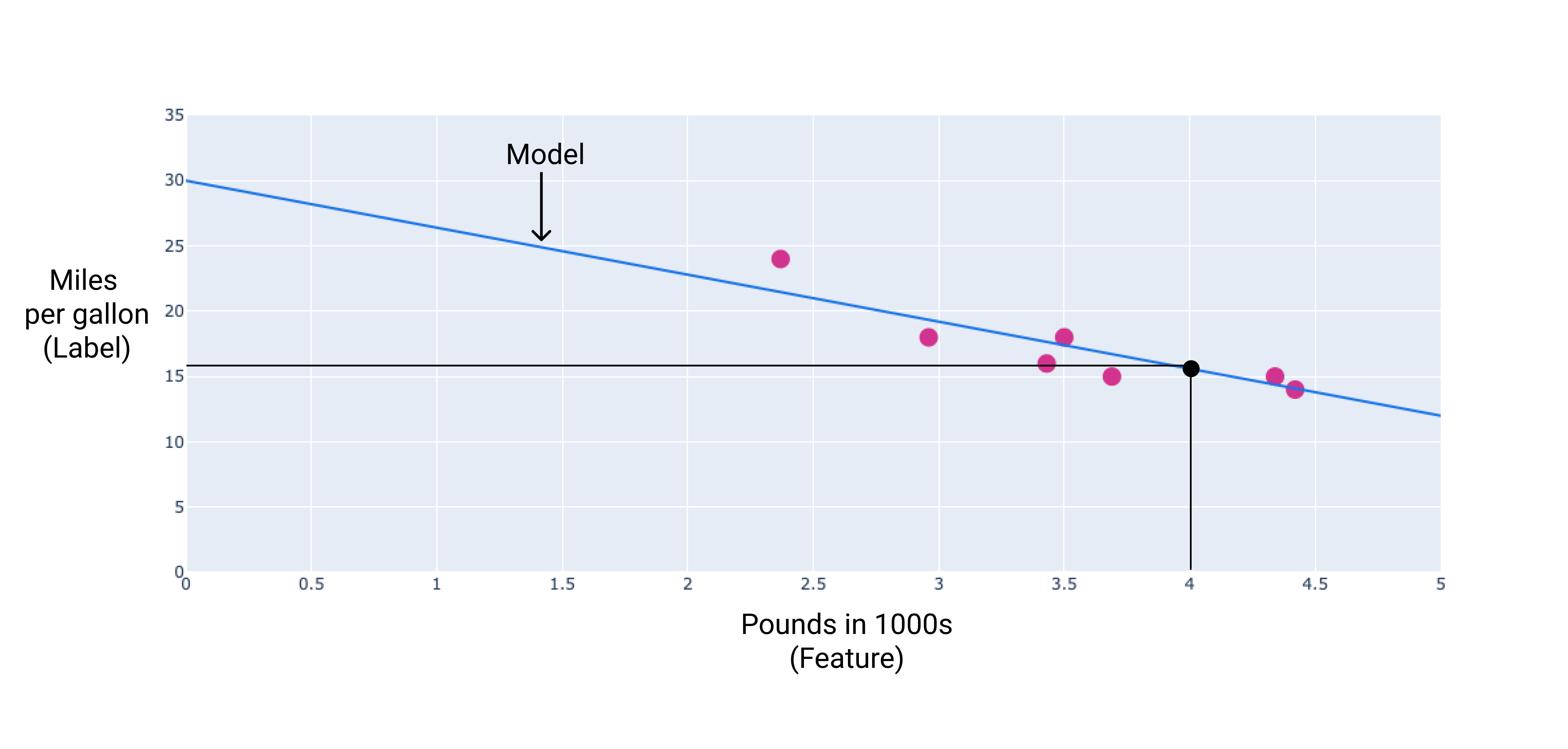
Figure 4. Selon le modèle, une voiture de 1 814 kg a une efficacité énergétique prévue de 15,6 miles par gallon.
Modèles avec plusieurs fonctionnalités
Bien que l'exemple de cette section n'utilise qu'une seule caractéristique (le poids de la voiture), un modèle plus sophistiqué peut s'appuyer sur plusieurs caractéristiques, chacune ayant un poids distinct ($ w_1 $, $ w_2 $, etc.). Par exemple, un modèle qui repose sur cinq caractéristiques s'écrirait comme suit :
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Par exemple, un modèle qui prédit la consommation de carburant pourrait également utiliser des caractéristiques telles que les suivantes :
- Cylindrée
- Accélération
- Nombre de cylindres
- Cheval-vapeur anglais
Ce modèle s'écrirait comme suit :
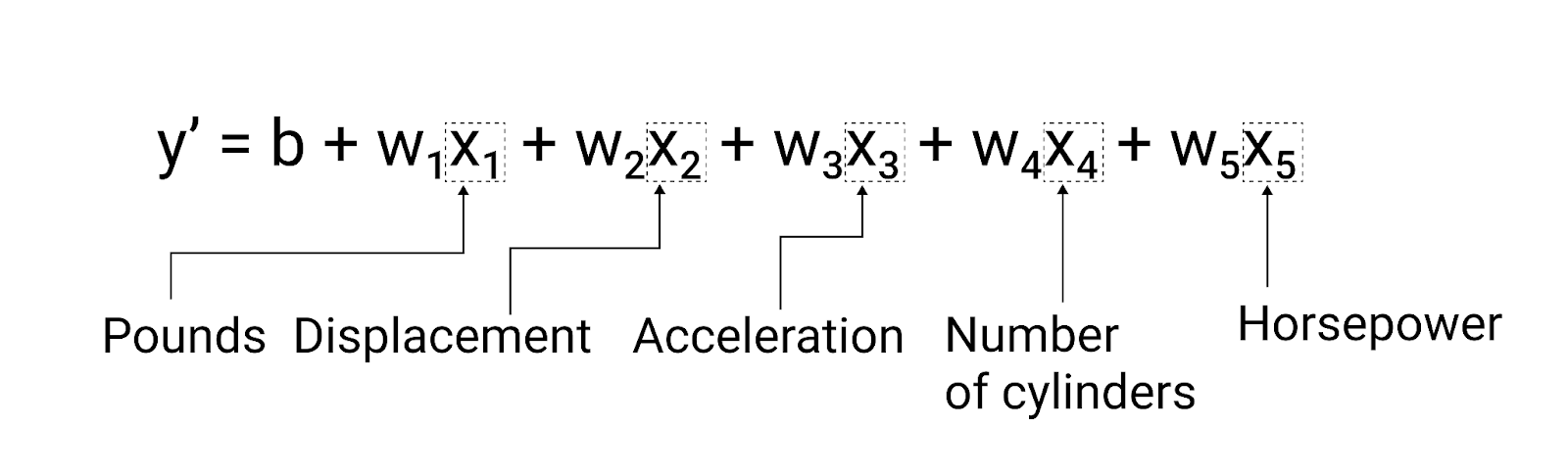
Figure 5. Modèle avec cinq caractéristiques permettant de prédire la consommation de carburant d'une voiture en miles par gallon.
En représentant graphiquement certaines de ces caractéristiques supplémentaires, nous pouvons constater qu'elles présentent également une relation linéaire avec le libellé (miles par gallon) :
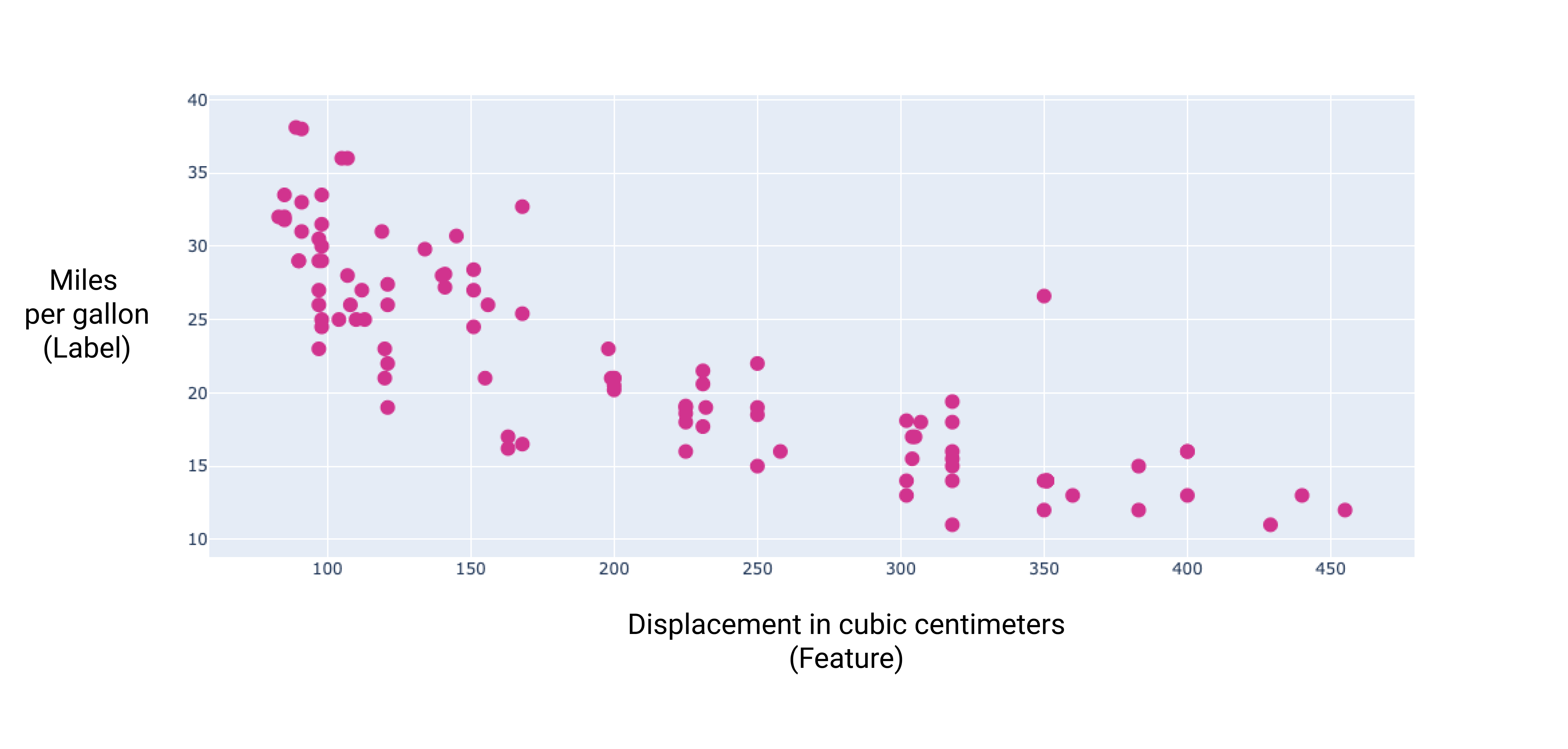
Figure 6. Cylindrée d'une voiture en centimètres cubes et consommation de carburant en miles par gallon. En général, plus le moteur d'une voiture est gros, plus sa consommation de carburant (en miles par gallon) est élevée.
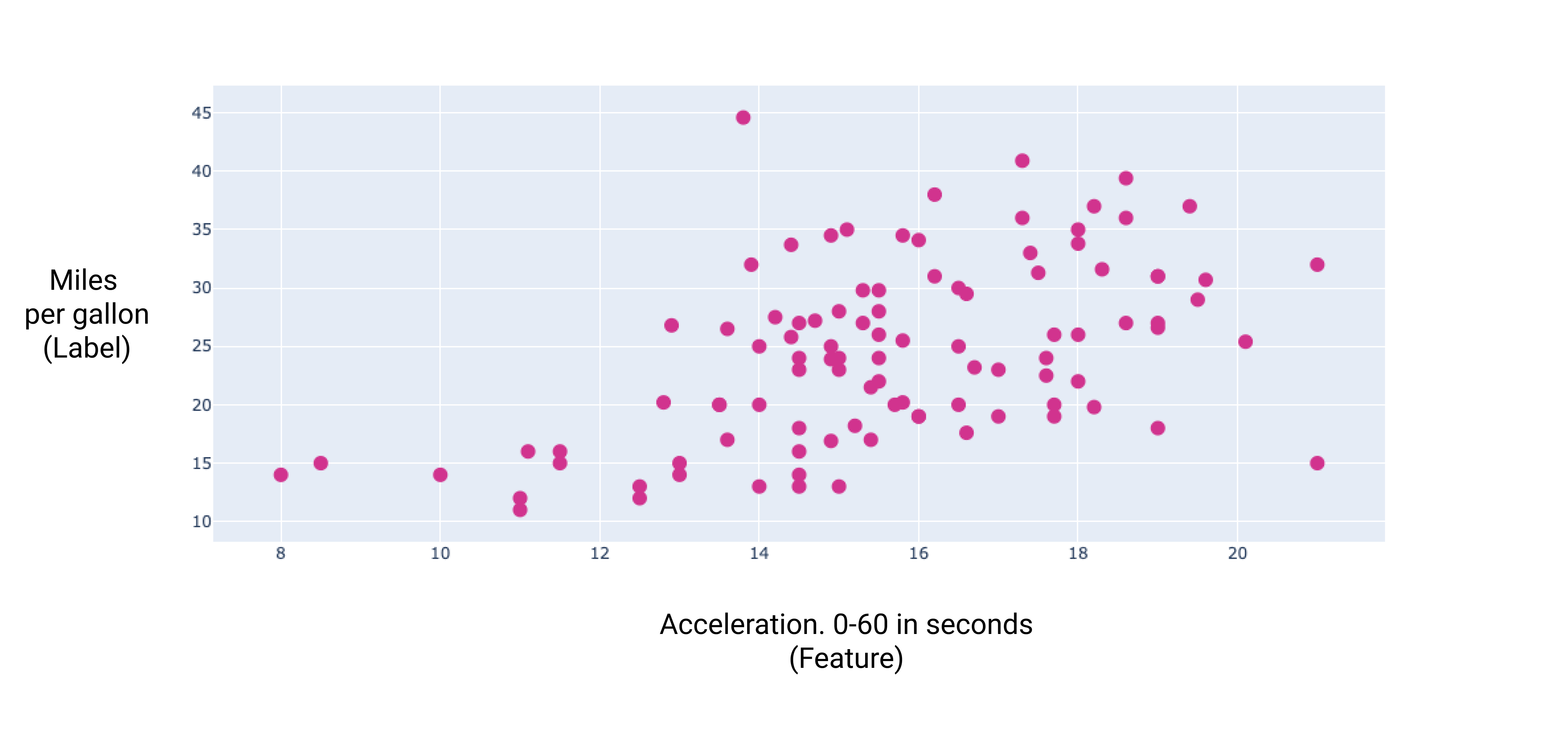
Figure 7 : L'accélération d'une voiture et sa consommation de carburant en miles par gallon. Plus l'accélération d'une voiture prend du temps, plus la consommation de carburant au kilomètre est généralement faible.