Muitos problemas exigem uma estimativa de probabilidade como saída. A regressão logística é um mecanismo extremamente eficiente para calcular probabilidades. Na prática, você pode usar a probabilidade retornada de uma destas duas maneiras:
Aplicado "como está". Por exemplo, se um modelo de previsão de spam receber um e-mail como entrada e gerar um valor de
0.932, isso implica uma probabilidade de93.2%de que o e-mail seja spam.Convertido em uma categoria binária, como
TrueouFalse,SpamouNot Spam.
Este módulo se concentra no uso da saída do modelo de regressão logística como está. No módulo de classificação, você vai aprender a converter essa saída em uma categoria binária.
Função sigmoide
Talvez você esteja se perguntando como um modelo de regressão logística pode garantir que a saída represente uma probabilidade, sempre gerando um valor entre 0 e 1. Existe uma família de funções chamada funções logísticas cuja saída tem essas mesmas características. A função logística padrão, também conhecida como função sigmoide (sigmoid significa "em forma de S"), tem a fórmula:
\[f(x) = \frac{1}{1 + e^{-x}}\]
em que:
- f(x) é a saída da função sigmoide.
- e é o número de Euler: uma constante matemática ≈ 2,71828.
- x é a entrada da função sigmoide.
A Figura 1 mostra o gráfico correspondente da função sigmoide.
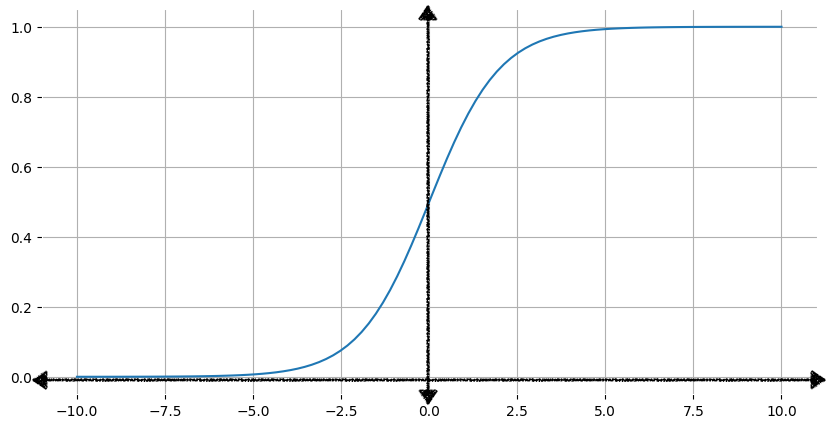
À medida que a entrada, x, aumenta, a saída da função sigmoide se aproxima de 1, mas nunca chega a esse valor. Da mesma forma, à medida que a entrada diminui, a saída da função sigmoide se aproxima, mas nunca atinge 0.
Clique aqui para saber mais sobre a matemática por trás da função sigmoide
A tabela abaixo mostra os valores de saída da função sigmoide para valores de entrada no intervalo de -7 a 7. Observe como a sigmoide se aproxima rapidamente de 0 para valores de entrada negativos decrescentes e de 1 para valores de entrada positivos crescentes.
No entanto, não importa o tamanho do valor de entrada, a saída sempre será maior que 0 e menor que 1.
| Entrada | Saída sigmoide |
|---|---|
| -7 | 0,001 |
| -6 | 0,002 |
| -5 | 0,007 |
| -4 | 0,018 |
| -3 | 0,047 |
| -2 | 0,119 |
| -1 | 0.269 |
| 0 | 0,50 |
| 1 | 0.731 |
| 2 | 0,881 |
| 3 | 0.952 |
| 4 | 0,982 |
| 5 | 0,993 |
| 6 | 0,997 |
| 7 | 0,999 |
Transformar a saída linear usando a função sigmoide
A equação a seguir representa o componente linear de um modelo de regressão logística:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
em que:
- z é a saída da equação linear, também chamada de odds logarítmicas.
- b é o viés.
- Os valores w são os pesos aprendidos do modelo.
- Os valores x são os valores de atributo de um exemplo específico.
Para obter a previsão de regressão logística, o valor z é transmitido à função sigmoide, gerando um valor (uma probabilidade) entre 0 e 1:
\[y' = \frac{1}{1 + e^{-z}}\]
em que:
- y' é a saída do modelo de regressão logística.
- e é o número de Euler: uma constante matemática ≈ 2,71828.
- z é a saída linear (conforme calculado na equação anterior).
Clique aqui para saber mais sobre log-odds
Na equação $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z é chamado de log-odds porque, se você começar com a seguinte função sigmoide (em que $y$ é a saída de um modelo de regressão logística, representando uma probabilidade):
$$y = \frac{1}{1 + e^{-z}}$$
Em seguida, resolva para z:
$$ z = \ln\left(\frac{y}{1-y}\right) $$
Então, z é definido como o logaritmo natural da razão entre as probabilidades dos dois resultados possíveis: y e 1 – y.
A Figura 2 ilustra como a saída linear é transformada em saída de regressão logística usando esses cálculos.
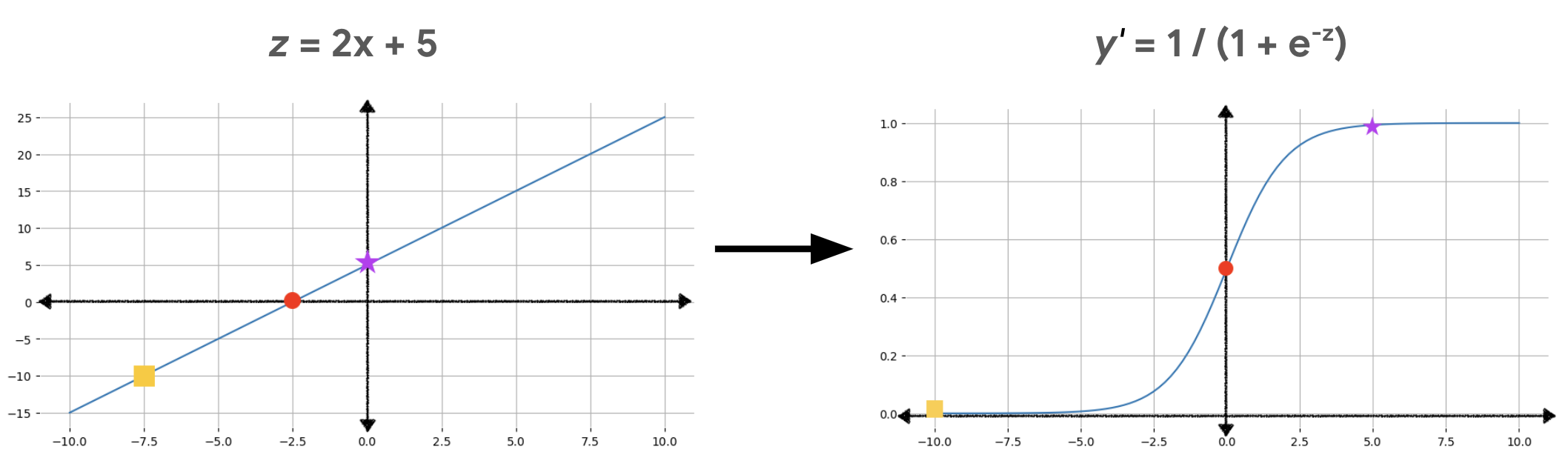
Na Figura 2, uma equação linear se torna entrada para a função sigmoide, que dobra a linha reta em uma forma de S. A equação linear pode gerar valores muito grandes ou muito pequenos de z, mas a saída da função sigmoide, y', está sempre entre 0 e 1, exclusivo. Por exemplo, o quadrado amarelo no gráfico à esquerda tem um valor z de -10, mas a função sigmoide no gráfico à direita mapeia esse -10 para um valor y' de 0,00004.
Exercício: teste de conhecimentos
Um modelo de regressão logística com três recursos tem o seguinte viés e pesos:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
Considerando os seguintes valores de entrada:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
Responda às duas perguntas a seguir.
Conforme calculado em #1 acima, o logito dos valores de entrada é 1. Substituindo esse valor de z na função sigmoide:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)