Нейронные сети: многоклассовая классификация

Ранее вы сталкивались с моделями двоичной классификации , которые могли выбирать между одним из двух возможных вариантов, например:

• Данное электронное письмо является спамом или не спамом.
• Данная опухоль бывает злокачественной или доброкачественной.

В этом разделе мы рассмотрим модели многоклассовой классификации , которые могут выбирать из нескольких возможностей. Например:

• Эта собака — бигль, бассет-хаунд или ищейка?
• Это цветок — сибирский ирис, голландский ирис, ирис «Голубой флаг» или карликовый бородатый ирис?
• Это самолет Боинг 747, Эйрбас 320, Боинг 777 или Эмбраер 190?
• Это изображение яблока, медведя, конфеты, собаки или яйца?

Некоторые реальные проблемы с несколькими классами влекут за собой выбор из миллионов отдельных классов. Например, рассмотрим модель классификации с несколькими классами, которая может идентифицировать изображение практически чего угодно.

В этом разделе подробно описаны два основных варианта многоклассовой классификации:

• один против всех
• один-против-одного , который обычно известен как softmax

Один против всех

Функция «Один против всех» позволяет использовать двоичную классификацию для серии прогнозов «да» или «нет» для нескольких возможных меток.

Учитывая задачу классификации с N возможными решениями, решение «один против всех» состоит из N отдельных двоичных классификаторов — по одному двоичному классификатору для каждого возможного результата. Во время обучения модель проходит через последовательность бинарных классификаторов, обучая каждый отвечать на отдельный вопрос классификации.

Например, по изображению фрукта можно обучить четыре разных распознавателя, каждый из которых будет отвечать на разные вопросы типа «да/нет»:

1. Это изображение яблоко?
2. Это изображение оранжевого цвета?
3. Это изображение банана?
4. Это изображение винограда?

На следующем изображении показано, как это работает на практике.

Рисунок 7. Изображение груши, передаваемое в качестве входных данных четырем различным двоичным классификаторам. Первая, вторая и четвертая модели (предсказывающие, является ли изображение яблоком, апельсином или виноградом соответственно) предсказывают отрицательный класс. Третья модель (предсказывающая, является ли изображение грушей) предсказывает положительный класс.

Дополнительные сведения о том, как бинарные классификаторы делают прогнозы (устанавливая порог классификации для преобразования выходных данных числовой модели в положительную или отрицательную метку), см. в модуле «Классификация» .

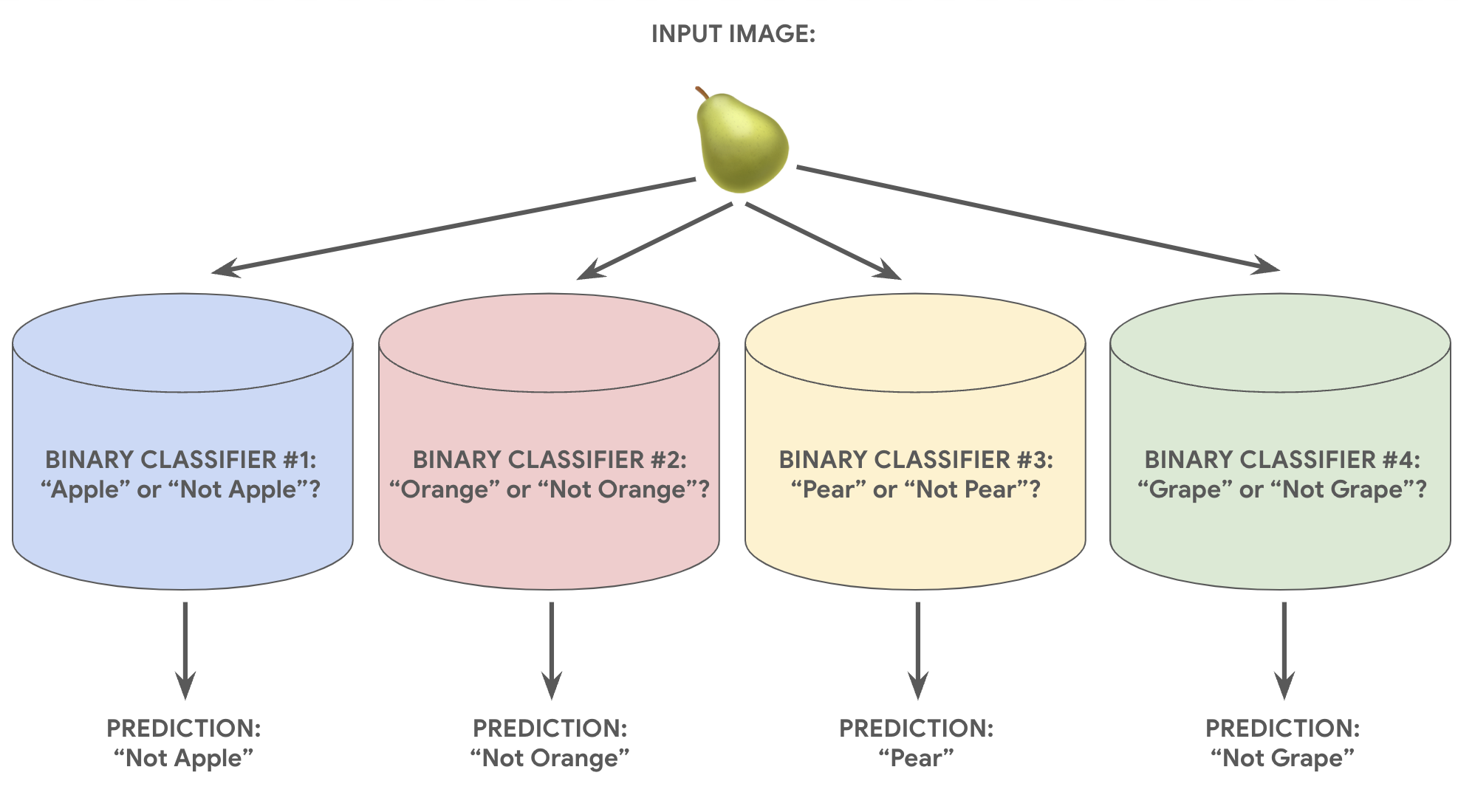
Этот подход вполне разумен, когда общее количество классов невелико, но становится все более неэффективным по мере увеличения числа классов.

Мы можем создать значительно более эффективную модель «один против всех» с глубокой нейронной сетью, в которой каждый выходной узел представляет отдельный класс. Следующее изображение иллюстрирует этот подход.

Рисунок 8. Те же задачи классификации «один против всех», выполненные с использованием модели нейронной сети. К выходному слою применяется сигмовидная функция активации, и каждое выходное значение представляет вероятность того, что входное изображение является указанным фруктом. Эта модель предсказывает, что существует 84% вероятность того, что изображение представляет собой грушу, и 7% вероятность того, что изображение представляет собой виноград.

Один против одного (софтмакс)

Возможно, вы заметили, что значения вероятности в выходном слое на рисунке 8 не составляют в сумме 1,0 (или 100%). (На самом деле их сумма равна 1,43.) При подходе «один против всех» вероятность каждого бинарного набора результатов определяется независимо от всех других наборов. То есть мы определяем вероятность «яблоко» и «не яблоко», не принимая во внимание вероятность других вариантов фруктов: «апельсин», «груша» или «виноград».

Но что, если мы хотим предсказать вероятности появления каждого фрукта относительно друг друга? В этом случае вместо прогнозирования «яблоко» против «не яблока» мы хотим предсказать «яблоко» против «апельсина» против «груши» против «винограда». Этот тип многоклассовой классификации называется классификацией «один против одного» .

Мы можем реализовать классификацию «один против одного», используя тот же тип архитектуры нейронной сети, который используется для классификации «один против всех», с одним ключевым изменением. Нам нужно применить другое преобразование к выходному слою.

В режиме «один против всех» мы применили функцию активации сигмоида к каждому выходному узлу независимо, что привело к получению выходного значения от 0 до 1 для каждого узла, но не гарантировало, что эти значения в сумме равны точно 1.

Вместо этого для решения «один против одного» мы можем применить функцию softmax , которая присваивает десятичные вероятности каждому классу в многоклассовой задаче так, что сумма всех вероятностей равна 1,0. Это дополнительное ограничение помогает обучению сходиться быстрее, чем в противном случае.

Нажмите значок плюса, чтобы увидеть уравнение softmax.

Уравнение softmax выглядит следующим образом:

$$p(y = j|\textbf{x}) = \frac{e^{(\textbf{w}_j^{T}\textbf{x} + b_j)}}{\sum_{k\in K} {e^{(\textbf{w}_k^{T}\textbf{x} + b_k)}} }$$

Обратите внимание, что эта формула по сути расширяет формулу логистической регрессии на несколько классов.

На следующем изображении наша задача многоклассовой классификации «один против всех» переосмыслена как задача «один против одного». Обратите внимание: для выполнения softmax скрытый слой, непосредственно предшествующий выходному слою (называемый слоем softmax), должен иметь то же количество узлов, что и выходной слой.

Рисунок 9. Реализация нейронной сети классификации «один на один» с использованием слоя softmax. Каждое выходное значение представляет собой вероятность того, что входное изображение является указанным фруктом, а не каким-либо из трех других фруктов (сумма всех вероятностей равна 1,0). Эта модель предсказывает, что вероятность того, что изображение будет грушей, составляет 63%.

Опции Софтмакс

Рассмотрим следующие варианты softmax:

• Полный softmax — это тот softmax, который мы обсуждали; то есть softmax вычисляет вероятность для каждого возможного класса.

• Выборка кандидатов означает, что softmax вычисляет вероятность для всех положительных меток, но только для случайной выборки отрицательных меток. Например, если мы заинтересованы в определении того, является ли входное изображение гончей или ищейкой, нам не нужно предоставлять вероятности для каждого примера, не являющегося собакой.

Полный softmax довольно дешев, когда количество классов невелико, но становится непомерно дорогим, когда количество классов увеличивается. Кандидатская выборка может повысить эффективность решения задач с большим количеством классов.

Один ярлык против множества ярлыков

Softmax предполагает, что каждый пример является членом ровно одного класса. Однако некоторые примеры могут одновременно быть членами нескольких классов. Для таких примеров:

• Вы не можете использовать softmax.
• Вы должны полагаться на множественные логистические регрессии.

Например, модель «один против одного» на рисунке 9 выше предполагает, что каждое входное изображение будет изображать ровно один тип фруктов: яблоко, апельсин, грушу или виноград. Однако если входное изображение может содержать несколько типов фруктов — миску с яблоками и апельсинами — вместо этого вам придется использовать несколько логистических регрессий.

Ключевые термины:

• Бинарная классификация
• Многоклассовая классификация
• Классификация «один против всех»
• softmax (классификация «один против одного»)