الشكل 1. مشكلة التصنيف غير الخطي لا يمكن للدالة الخطية
فصل جميع النقاط الزرقاء عن النقاط البرتقالية بوضوح.
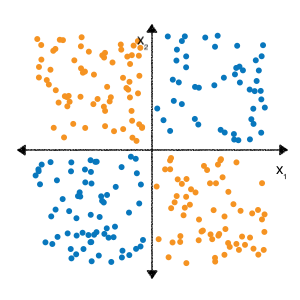
تعني "غير خطي" أنّه لا يمكنك التنبؤ بدقة بتصنيف باستخدام
نموذج للنموذج \(b + w_1x_1 + w_2x_2\). أو بعبارةٍ أخرى،
"مساحة القرار" ليس خطًا.
ومع ذلك، إذا أجرينا تقاطع خاصية على الميزتين $x_1$ و $x_2$، فيمكننا
ومن ثم تمثيل العلاقة غير الخطية بين العنصرين باستخدام
نموذج المساواة بين نقاط الاتصال:
$b + w_1x_1 + w_2x_2 + w_3x_3$ حيث $x_3$ هو تقاطع الميزة بين
$x_1$ و $x_2$:
الشكل 2. من خلال إضافة تقاطع الخصائص
س1س2، يمكن أن يتعلم النموذج الخطي
شكل زائدي يفصل النقاط الزرقاء عن النقاط البرتقالية.
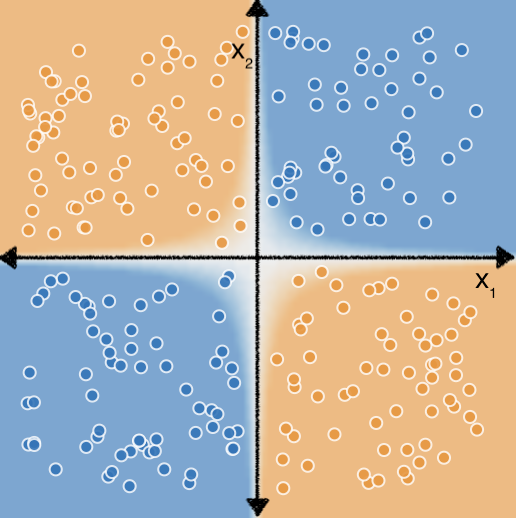
لنلقِ نظرة الآن على مجموعة البيانات التالية:
الشكل 3. مشكلة تصنيف غير خطي أكثر صعوبة
قد تتذكر أيضًا من تمارين متعددة الميزات
أن تحديد الميزة الصحيحة يتقاطع لملاءمة أي نموذج خطي مع هذه البيانات
واستغرقت المزيد من الجهد والتجربة.
ولكن ماذا لو لم يكن عليك إجراء كل هذه التجارب بنفسك؟
الشبكات العصبية هي مجموعة
من تصاميم النماذج المصمّمة للعثور على
أنماط غير خطية
في البيانات. أثناء تدريب شبكة عصبية، يتعرّف
النموذج تلقائيًا
على عمليات تقاطع الميزات المثلى لاستخدامها في بيانات الإدخال لتقليل
الخسارة.
في الأقسام التالية، سنلقي نظرة عن كثب على آلية عمل الشبكات العصبونية.
تاريخ التعديل الأخير: 2025-07-27 (حسب التوقيت العالمي المتفَّق عليه)
[null,null,["تاريخ التعديل الأخير: 2025-07-27 (حسب التوقيت العالمي المتفَّق عليه)"],[[["\u003cp\u003eThis module explores neural networks, a model architecture designed to automatically identify nonlinear patterns in data, eliminating the need for manual feature cross experimentation.\u003c/p\u003e\n"],["\u003cp\u003eYou will learn the fundamental components of a deep neural network, including nodes, hidden layers, and activation functions, and how they contribute to prediction.\u003c/p\u003e\n"],["\u003cp\u003eThe module covers the training process of neural networks, using the backpropagation algorithm to optimize predictions and minimize loss.\u003c/p\u003e\n"],["\u003cp\u003eAdditionally, you will gain insights into how neural networks handle multi-class classification problems using one-vs.-all and one-vs.-one approaches.\u003c/p\u003e\n"],["\u003cp\u003eThis module builds on prior knowledge of machine learning concepts such as linear and logistic regression, classification, and working with numerical and categorical data.\u003c/p\u003e\n"]]],[],null,["# Neural networks\n\n| **Estimated module length:** 75 minutes\n| **Learning objectives**\n|\n| - Explain the motivation for building neural networks, and the use cases they address.\n| - Define and explain the function of the key components of a deep neural network architecture:\n| - **[Nodes](/machine-learning/glossary#node-neural-network)**\n| - **[Hidden layers](/machine-learning/glossary#hidden_layer)**\n| - **[Activation functions](/machine-learning/glossary#activation_function)**\n| - Develop intuition around how neural network predictions are made, by stepping through the inference process.\n| - Build a high-level intuition of how neural networks are trained, using the backpropagation algorithm.\n| - Explain how neural networks can be used to perform two types of multi-class classification: one-vs.-all and one-vs.-one.\n| **Prerequisites:**\n|\n| This module assumes you are familiar with the concepts covered in the\n| following modules:\n|\n| - [Introduction to Machine Learning](/machine-learning/intro-to-ml)\n| - [Linear regression](/machine-learning/crash-course/linear-regression)\n| - [Logistic regression](/machine-learning/crash-course/logistic-regression)\n| - [Classification](/machine-learning/crash-course/classification)\n| - [Working with numerical data](/machine-learning/crash-course/numerical-data)\n| - [Working with categorical data](/machine-learning/crash-course/categorical-data)\n| - [Datasets, generalization, and overfitting](/machine-learning/crash-course/overfitting)\n\nYou may recall from the\n[Feature cross exercises](/machine-learning/crash-course/categorical-data/feature-cross-exercises)\nin the [Categorical data module](/machine-learning/crash-course/categorical-data),\nthat the following classification problem is nonlinear:\n**Figure 1.** Nonlinear classification problem. A linear function cannot cleanly separate all the blue dots from the orange dots.\n\n\"Nonlinear\" means that you can't accurately predict a label with a\nmodel of the form \\\\(b + w_1x_1 + w_2x_2\\\\). In other words, the\n\"decision surface\" is not a line.\n\nHowever, if we perform a feature cross on our features $x_1$ and $x_2$, we can\nthen represent the nonlinear relationship between the two features using a\n[**linear model**](/machine-learning/glossary#linear-model):\n$b + w_1x_1 + w_2x_2 + w_3x_3$ where $x_3$ is the feature cross between\n$x_1$ and $x_2$:\n**Figure 2.** By adding the feature cross *x* ~1~*x* ~2~, the linear model can learn a hyperbolic shape that separates the blue dots from the orange dots.\n\nNow consider the following dataset:\n**Figure 3.** A more difficult nonlinear classification problem.\n\nYou may also recall from the [Feature cross exercises](/machine-learning/crash-course/categorical-data/feature-cross-exercises)\nthat determining the correct feature crosses to fit a linear model to this data\ntook a bit more effort and experimentation.\n\nBut what if you didn't have to do all that experimentation yourself?\n[**Neural networks**](/machine-learning/glossary#neural_network) are a family\nof model architectures designed to find\n[**nonlinear**](/machine-learning/glossary#nonlinear)\npatterns in data. During training of a neural network, the\n[**model**](/machine-learning/glossary#model) automatically\nlearns the optimal feature crosses to perform on the input data to minimize\nloss.\n\nIn the following sections, we'll take a closer look at how neural networks work.\n| **Key terms:**\n|\n| - [Activation function](/machine-learning/glossary#activation_function)\n| - [Hidden layer](/machine-learning/glossary#hidden_layer)\n| - [Linear model](/machine-learning/glossary#linear-model)\n| - [Model](/machine-learning/glossary#model)\n| - [Neural network](/machine-learning/glossary#neural_network)\n| - [Nodes](/machine-learning/glossary#node-neural-network)\n- [Nonlinear](/machine-learning/glossary#nonlinear) \n[Help Center](https://support.google.com/machinelearningeducation)"]]
