Binning (auch Bucketing genannt) ist ein
Feature Engineering
Verfahren, das verschiedene numerische Teilbereiche in Bins oder
Buckets:
In vielen Fällen werden numerische Daten beim Binning in kategorische Daten umgewandelt.
Sehen wir uns zum Beispiel eine Funktion an.
namens X, deren niedrigster Wert 15 ist und
der höchste Wert bei 425 liegt. Mithilfe von Binning könnten Sie X mit der
folgende fünf Container:
- Container 1: 15–34
- Container 2: 35 bis 117
- Container 3: 118 bis 279
- Container 4: 280 bis 392
- Container 5: 393 bis 425
Container 1 umfasst den Bereich von 15 bis 34, sodass jeder Wert von X zwischen 15 und 34 liegt.
in Container 1 landet. Ein auf diesen Klassen trainiertes Modell reagiert nicht anders
auf die X-Werte 17 und 29, da sich beide Werte in Container 1 befinden.
Der Featurevektor repräsentiert auf die fünf Container:
| Klassennummer | Bereich | Featurevektor |
|---|---|---|
| 1 | 15-34 | [1,0, 0,0, 0,0, 0,0, 0,0] |
| 2 | 35-117 | [0,0, 1,0, 0,0, 0,0, 0,0] |
| 3 | 118-279 | [0,0, 0,0, 1,0, 0,0, 0,0] |
| 4 | 280-392 | [0,0, 0,0, 0,0, 1,0, 0,0] |
| 5 | 393-425 | [0,0, 0,0, 0,0, 0,0, 1,0] |
Obwohl X eine einzelne Spalte im Dataset ist, verursacht Binning ein Modell.
um X als fünf separate Funktionen zu behandeln. Daher lernt das Modell
separate Gewichte für jeden Container.
Gruppieren ist eine gute Alternative zur Skalierung. oder clipping, wenn entweder erfüllt sind:
- Die allgemeine lineare Beziehung zwischen dem Element und dem Element Das Label label ist schwach oder nicht vorhanden.
- Wenn die Featurewerte geclustert sind.
Das Gruppieren ist unlogisch, da das Modell im im vorherigen Beispiel die Werte 37 und 115 gleich behandelt. Wenn Sie jedoch ein Element un umständlicher als ein lineares Element erscheint, ist Gruppierung eine viel bessere Möglichkeit, die die Daten darstellen.
Beispiel für Gruppierung: Anzahl der Käufer im Vergleich zur Temperatur
Angenommen, Sie erstellen ein Modell, das die Anzahl der Käufer nach der Außentemperatur an diesem Tag. Hier ist ein Diagramm der im Vergleich zur Anzahl der Käufer:
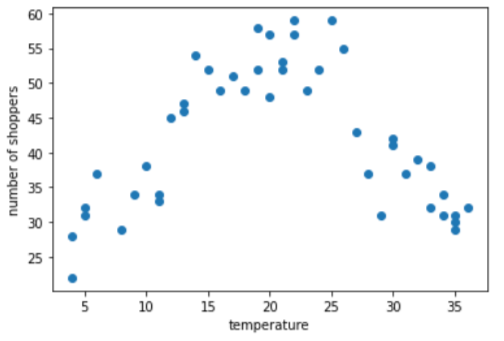
Das Diagramm zeigt, nicht überraschend, dass die Anzahl der Käufer am höchsten war, war die Temperatur am angenehmsten.
Sie könnten das Merkmal als Rohwerte darstellen: eine Temperatur von 35,0 im wäre im Featurevektor 35,0. Ist das die beste Idee?
Während des Trainings lernt ein lineares Regressionsmodell für jede . Wird die Temperatur als einzelnes Merkmal dargestellt, ist also ein eine Temperatur von 35,0 hat den fünffachen Einfluss (oder ein Fünftel der Einfluss) in einer Vorhersage als Temperatur von 7,0. Das Diagramm zeigt jedoch jede Art von linearer Beziehung zwischen dem Label und dem Featurewert.
Im Diagramm werden drei Cluster in den folgenden Teilbereichen vorgeschlagen:
- Container 1 ist der Temperaturbereich von 4 bis 11.
- Container 2 ist der Temperaturbereich von 12 bis 26.
- Container 3 ist der Temperaturbereich 27–36.

Das Modell lernt separate Gewichte für jeden Container.
Es ist zwar möglich, mehr als drei Klassen zu erstellen, auch für Temperatur messen, ist dies aus folgenden Gründen oft eine schlechte Idee:
- Ein Modell kann die Verknüpfung zwischen einem Container und einem Label nur dann lernen, wenn Beispiele dafür sind. In diesem Beispiel hat jeder der drei Container enthält mindestens 10 Beispiele, die möglicherweise für das Training ausreichen. Mit 33 separaten Behältern Keiner der Container würde genügend Beispiele für das Training des Modells enthalten.
- Ein separater Behälter für jede Temperatur führt zu 33 separate Temperaturfunktionen. In der Regel sollten Sie jedoch minimieren, die Anzahl der Merkmale in einem Modell.
Übung: Wissenstest
Das folgende Diagramm zeigt den Medianwert der Immobilienpreise pro 0,2 Grad Breitengrad für das sagenhafte Land Freedonia:
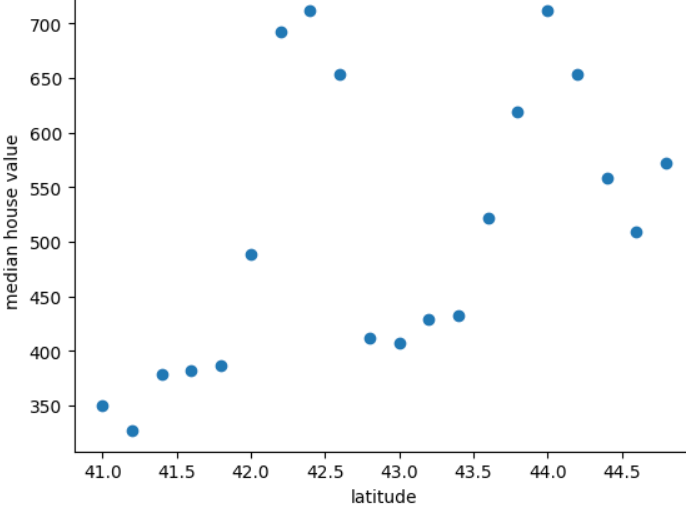 <ph type="x-smartling-placeholder">
<ph type="x-smartling-placeholder">Die Grafik zeigt ein nicht lineares Muster zwischen Basiswert und Breitengrad, Es ist daher unwahrscheinlich, dass die Darstellung des Breitengrads als Gleitkommawert hilfreich ist. um gute Vorhersagen zu machen. Vielleicht wäre das Bucketing von Breitengraden Idee?
- 41,0 bis 41,8
- 42,0 bis 42,6
- 42,8 bis 43,4
- 43,6 bis 44,8
Quantil-Bucketing
Beim Quantilen Bucketing werden Bucketing-Grenzen erstellt, sodass die Anzahl der Beispiele in jedem Bucket genau oder nahezu gleich ist. Quantil-Bucketing die Ausreißer größtenteils ausgeblendet.
Um das Problem zu veranschaulichen, das sich durch Quantil-Bucketing lösen lässt, betrachten wir das wie in der folgenden Abbildung dargestellt, in denen jeweils der zehn Buckets eine Spanne von genau 10.000 $. Beachten Sie,dass der Bucket von 0 bis 10.000 Dutzende von Beispielen enthält. aber der Bucket von 50.000 bis 60.000 enthält nur fünf Beispiele. Daher hat das Modell genug Beispiele, um mit den Werten von 0 bis 10.000 Bucket, aber nicht genügend Beispiele zum Trainieren für den Bucket von 50.000 bis 60.000.
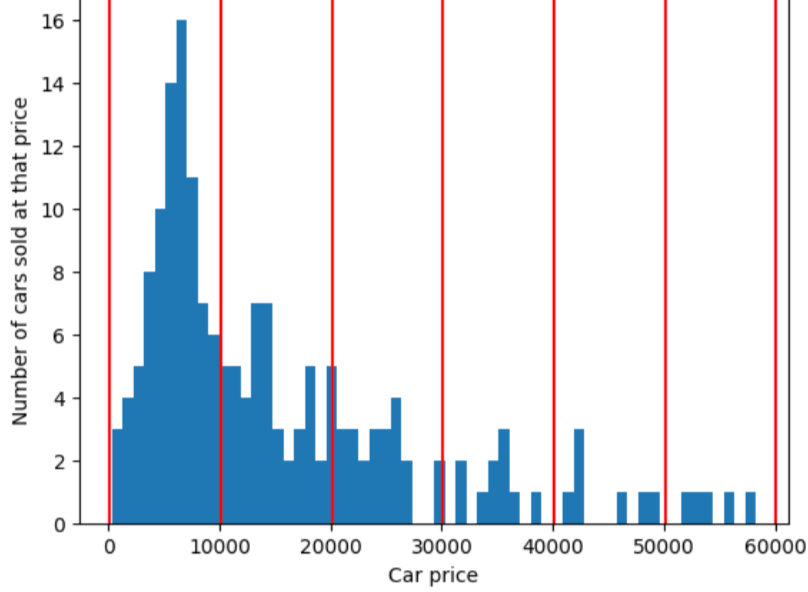 <ph type="x-smartling-placeholder">
<ph type="x-smartling-placeholder">Im Gegensatz dazu wird in der folgenden Abbildung das Quantil-Bucketing zur Aufteilung der Autopreise verwendet in Klassen mit ungefähr derselben Anzahl von Beispielen in jedem Bucket aufzuteilen. Beachten Sie, dass einige Klassen eine enge Preisspanne haben, während andere eine sehr große Preisspanne umfassen.
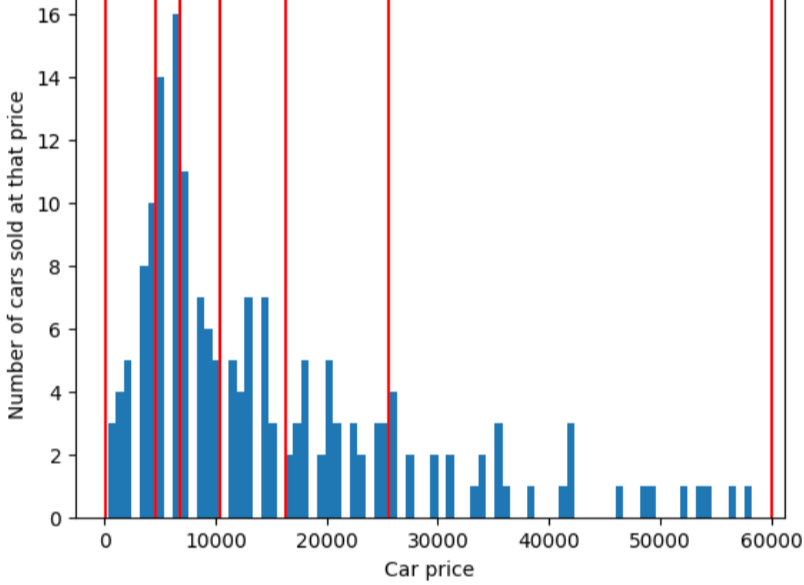 <ph type="x-smartling-placeholder">
<ph type="x-smartling-placeholder">