Numerische Daten: Normalisierung

Nachdem Sie Ihre Daten mithilfe statistischer und Visualisierungstechniken untersucht haben, sollten Sie sie so transformieren, dass Ihr Modell effektiver trainiert werden kann. Ziel der Normalisierung ist es, die Funktionen auf eine ähnliche Skala zu transformieren. Betrachten Sie beispielsweise die folgenden beiden Funktionen:

• Die Funktion X umfasst den Bereich von 154 bis 24.917.482.
• Das Element Y umfasst den Bereich 5 bis 22.

Diese beiden Funktionen haben sehr unterschiedliche Bereiche. Bei der Normalisierung werden X und Y möglicherweise so manipuliert, dass sie einen ähnlichen Bereich abdecken, z. B. 0 bis 1.

Die Normalisierung bietet folgende Vorteile:

• Hilft dabei, Modelle während des Trainings schneller zu konvergieren. Wenn verschiedene Funktionen unterschiedliche Bereiche haben, kann der Gradientenabstieg „abprallen“ und die Konvergenz verlangsamen. Fortgeschrittenere Optimierer wie Adagrad und Adam schützen jedoch vor diesem Problem, indem sie die effektive Lernrate im Laufe der Zeit ändern.
• Hilft Modellen, bessere Vorhersagen zu treffen. Wenn verschiedene Funktionen unterschiedliche Bereiche haben, sind die Vorhersagen des resultierenden Modells möglicherweise weniger nützlich.
• Hilft, die NaN-Falle zu vermeiden, wenn die Attributwerte sehr hoch sind. NaN ist eine Abkürzung für Not a Number (keine Zahl). Wenn ein Wert in einem Modell die Grenze der Gleitkommapräzision überschreitet, setzt das System den Wert auf NaN statt auf eine Zahl. Wenn eine Zahl im Modell zu einem NaN wird, werden auch andere Zahlen im Modell irgendwann zu einem NaN.
• Hilft dem Modell, entsprechende Gewichtungen für jedes Merkmal zu lernen. Ohne Merkmalskalierung schenkt das Modell Merkmalen mit großen Bereichen zu viel Aufmerksamkeit und Merkmalen mit schmalen Bereichen zu wenig.

Wir empfehlen, numerische Features zu normalisieren, die deutlich unterschiedliche Bereiche abdecken (z. B. Alter und Einkommen). Wir empfehlen auch, ein einzelnes numerisches Merkmal zu normalisieren, das einen großen Bereich abdeckt, z. B. city population..

Warnung: Wenn Sie ein Merkmal während des Trainings normalisieren, müssen Sie es auch bei der Vorhersage normalisieren.

Betrachten Sie die folgenden beiden Funktionen:

• Der niedrigste Wert für das Element A ist −0,5 und der höchste Wert ist +0,5.
• Der niedrigste Wert für das Element B ist −5,0 und der höchste Wert ist +5,0.

Die Spannweite von Feature A und Feature B ist relativ gering. Die Spanne von Element B ist jedoch zehnmal so breit wie die von Element A. Beispiele:

• Zu Beginn des Trainings geht das Modell davon aus, dass Merkmal B zehnmal „wichtiger“ ist als Merkmal A.
• Das Training dauert länger als es sollte.
• Das resultierende Modell ist möglicherweise nicht optimal.

Die Gesamtauswirkungen der fehlenden Normalisierung sind relativ gering. Wir empfehlen jedoch, Merkmal A und Merkmal B auf dieselbe Skala zu normalisieren, z. B. -1,0 bis +1,0.

Betrachten wir nun zwei Funktionen mit einem größeren Unterschied zwischen den Bereichen:

• Der niedrigste Wert für das Element C ist −1 und der höchste Wert ist +1.
• Der niedrigste Wert für das Element D ist +5.000 und der höchste Wert ist +1.000.000.000.

Wenn Sie das Attribut C und das Attribut D nicht normalisieren, ist Ihr Modell wahrscheinlich nicht optimal. Außerdem dauert es viel länger, bis das Training konvergiert, oder es konvergiert gar nicht.

In diesem Abschnitt werden drei gängige Normalisierungsmethoden behandelt:

• lineare Skalierung
• Z-Score-Skalierung
• Logarithmische Skalierung

In diesem Abschnitt wird außerdem Zuschneiden behandelt. Obwohl es sich nicht um eine echte Normalisierungstechnik handelt, werden durch das Zuschneiden unruhige numerische Merkmale in Bereiche eingegrenzt, die bessere Modelle ergeben.

Lineare Skalierung

Bei der linearen Skalierung (häufig auch nur Skalierung genannt) werden Gleitkommawerte aus ihrem natürlichen Bereich in einen Standardbereich umgewandelt, in der Regel 0 bis 1 oder −1 bis +1.

Klicken Sie auf das Symbol, um die Mathematik zu sehen.

Verwenden Sie die folgende Formel, um auf den Standardbereich von 0 bis 1 zu skalieren:

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

Dabei gilt:

• $x'$ ist der skalierte Wert.
• „x“ ist der ursprüngliche Wert.
• $x_{min}$ ist der niedrigste Wert im Datensatz dieser Funktion.
• $x_{max}$ ist der höchste Wert im Datensatz dieser Funktion.

Angenommen, Sie haben ein Feature namens quantity, dessen natürlicher Bereich von 100 bis 900 reicht. Angenommen, der natürliche Wert von quantity in einem bestimmten Beispiel ist 300. Der normalisierte Wert von 300 wird daher so berechnet:

• $x$ = 300
• $x_{min}$ = 100
• $x_{max}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

---

Die lineare Skalierung ist eine gute Wahl, wenn alle der folgenden Bedingungen erfüllt sind:

• Die Unter- und Obergrenzen Ihrer Daten ändern sich im Laufe der Zeit nicht wesentlich.
• Das Feature enthält wenige oder keine Ausreißer und diese Ausreißer sind nicht extrem.
• Die Merkmale sind im gesamten Bereich ungefähr gleichmäßig verteilt. Das heißt, ein Histogramm würde für die meisten Werte ungefähr gleichmäßige Balken zeigen.

Angenommen, age ist eine Funktion. Die lineare Skalierung ist ein gutes Normalisierungsverfahren für age, weil:

• Die ungefähren Unter- und Obergrenzen sind 0 bis 100.
• age enthält einen relativ geringen Prozentsatz an Ausreißern. Nur etwa 0,3% der Bevölkerung sind älter als 100 Jahre.
• Bestimmte Altersgruppen sind zwar etwas besser vertreten als andere, ein großer Datensatz sollte jedoch genügend Beispiele für alle Altersgruppen enthalten.

Hinweis: Die meisten realen Funktionen erfüllen nicht alle Kriterien für die lineare Skalierung. Die Z-Score-Skalierung ist in der Regel eine bessere Normalisierungsmethode als die lineare Skalierung.

Übung: Wissen testen

Angenommen, Ihr Modell hat ein Feature namens net_worth, das das Nettovermögen verschiedener Personen enthält. Wäre die lineare Skalierung eine gute Normalisierungstechnik für net_worth? Warum bzw. warum nicht?

Klicken Sie auf das Symbol, um die Antwort zu sehen.

Antwort:Die lineare Skalierung ist für die Normalisierung von net_worth nicht geeignet. Diese Funktion enthält viele Ausreißer und die Werte sind nicht gleichmäßig über den primären Bereich verteilt. Die meisten Menschen würden in einem sehr schmalen Bereich des Gesamtbereichs eingeklemmt.

---

Z-Score-Skalierung

Ein Z-Wert ist die Anzahl der Standardabweichungen eines Werts vom Mittelwert. Ein Wert, der beispielsweise 2 Standardabweichungen über dem Mittelwert liegt, hat einen Z-Wert von +2,0. Ein Wert, der 1,5 Standardabweichungen unter dem Mittelwert liegt, hat einen Z-Wert von −1,5.

Wenn ein Feature mit Z-Score-Skalierung dargestellt wird, wird der Z-Score dieses Features im Featurevektor gespeichert. Die folgende Abbildung zeigt beispielsweise zwei Histogramme:

• Links sehen Sie eine klassische Normalverteilung.
• Rechts ist dieselbe Verteilung zu sehen, die durch Z-Score-Skalierung normalisiert wurde.

Abbildung 4: Rohdaten (links) im Vergleich zum Z-Wert (rechts) für eine normale Verteilung.

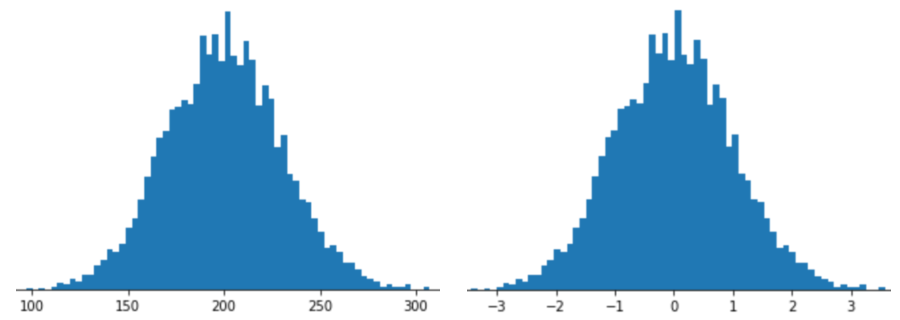
Die Z-Score-Skalierung eignet sich auch für Daten wie in der folgenden Abbildung, die nur eine ungenau normale Verteilung haben.

Abbildung 5: Rohdaten (links) im Vergleich zur Z-Wert-Skalierung (rechts) für eine nicht klassische Normalverteilung.

Klicken Sie auf das Symbol, um die Mathematik zu sehen.

Mit der folgenden Formel können Sie einen Wert „x“ auf seinen Z-Wert normalisieren:

$$ x' = (x - μ) / σ $$

Dabei gilt:

• $x'$ ist der Z-Wert.
• „x“ ist der Rohwert, also der Wert, der normalisiert wird.
• μ ist der Mittelwert.
• σ ist die Standardabweichung.

Angenommen, folgende Bedingungen sind erfüllt:

• mean = 100
• Standardabweichung = 20
• original value = 130

Beispiele:

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

---

Klicken Sie auf das Symbol, um mehr über Normalverteilungen zu erfahren.

Bei einer klassischen Normalverteilung:

• Mindestens 68,27% der Daten haben einen Z-Wert zwischen −1,0 und +1,0.
• Mindestens 95,45% der Daten haben einen Z-Wert zwischen −2,0 und +2,0.
• Bei mindestens 99,73% der Daten liegt der Z-Wert zwischen -3,0 und +3,0.
• Bei mindestens 99,994% der Daten liegt der Z-Wert zwischen -4,0 und +4,0.

Datenpunkte mit einem Z-Wert von weniger als −4, 0 oder mehr als +4, 0 sind also selten. Sind sie aber wirklich Ausreißer? Da Ausbrüche ein Konzept ohne strenge Definition ist, kann das niemand mit Sicherheit sagen. Beachten Sie, dass ein Dataset mit einer ausreichend großen Anzahl von Beispielen mit ziemlicher Sicherheit mindestens einige dieser „seltenen“ Beispiele enthält. Ein Feature mit einer Milliarde Beispielen, die einer klassischen Normalverteilung entsprechen, kann beispielsweise bis zu 60.000 Beispiele mit einem Wert außerhalb des Bereichs von -4,0 bis +4,0 haben.

---

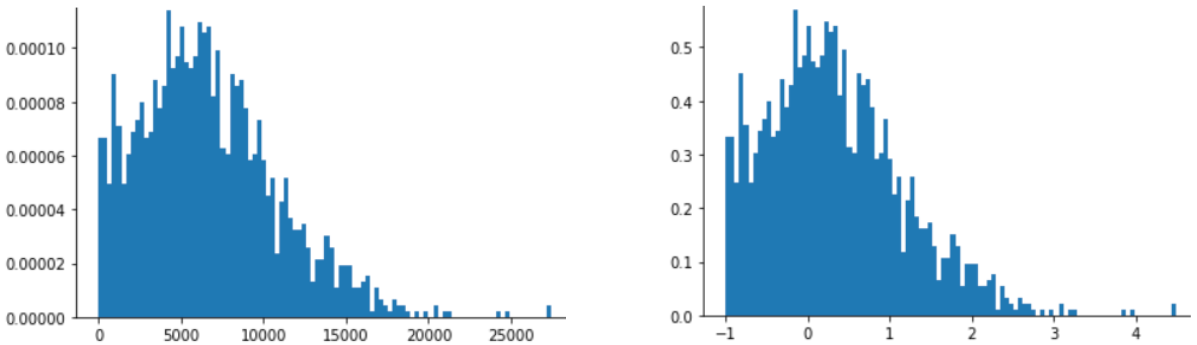
Der Z-Wert eignet sich gut, wenn die Daten einer Normalverteilung oder einer Verteilung folgen, die einer Normalverteilung ähnelt.

Einige Verteilungen können im Großteil ihres Bereichs normal sein, aber dennoch extreme Ausreißer enthalten. So können beispielsweise fast alle Punkte eines net_worth-Features genau in drei Standardabweichungen passen, aber einige Beispiele für dieses Feature können sich hunderte von Standardabweichungen vom Mittelwert entfernen. In diesen Fällen können Sie die Z-Score-Skalierung mit einer anderen Form der Normalisierung (in der Regel Clipping) kombinieren, um diese Situation zu bewältigen.

Übung: Wissen testen

Angenommen, Ihr Modell wird mit einem Feature namens height trainiert, das die Erwachsenengrößen von zehn Millionen Frauen enthält. Wäre die Z-Score-Skalierung eine gute Normalisierungsmethode für height? Warum bzw. warum nicht?

Klicken Sie auf das Symbol, um die Antwort zu sehen.

Antwort:Die Z-Score-Skalierung wäre eine gute Normalisierungstechnik für height, da dieses Merkmal einer Normalverteilung entspricht. Zehn Millionen Beispiele bedeuten viele Ausreißer – wahrscheinlich genug Ausreißer, damit das Modell Muster bei sehr hohen oder sehr niedrigen Z-Werten lernen kann.

---

Logarithmische Skalierung

Bei der Logarithmusskala wird der Logarithmus des Rohwerts berechnet. Theoretisch kann der Logarithmus jede beliebige Basis haben. In der Praxis wird bei der Logarithmusskala in der Regel der natürliche Logarithmus (ln) berechnet.

Klicken Sie auf das Symbol, um die Mathematik zu sehen.

Mit der folgenden Formel können Sie einen Wert x auf seinen Logarithmus normieren:

$$ x' = ln(x) $$

Dabei gilt:

• $x'$ ist der natürliche Logarithmus von $x$.
• original value = 54.598

Daher beträgt der Logarithmus des ursprünglichen Werts etwa 4, 0:

  4.0 = ln(54.598)

---

Die Logarithmusskala ist hilfreich, wenn die Daten einer Potenzgesetzverteilung folgen. Eine Potenzverteilung sieht in etwa so aus:

• Niedrige Werte von X haben sehr hohe Werte von Y.
• Wenn die Werte von X steigen, sinken die Werte von Y schnell. Hohe Werte von X haben daher sehr niedrige Werte von Y.

Filmbewertungen sind ein gutes Beispiel für eine Potenzgesetzverteilung. Beachten Sie in der folgenden Abbildung Folgendes:

• Einige Filme haben viele Nutzerbewertungen. Niedrige Werte für X haben hohe Werte für Y.
• Die meisten Filme haben nur sehr wenige Nutzerbewertungen. Hohe Werte für X haben niedrige Werte für Y.

Durch die Logarithmustransformation wird die Verteilung geändert, was dazu beiträgt, ein Modell zu trainieren, das bessere Vorhersagen trifft.

Abbildung 6: Vergleich einer Rohverteilung mit dem zugehörigen Log.

Als zweites Beispiel: Buchverkäufe folgen einer Potenzverteilung, weil:

• Die meisten veröffentlichten Bücher werden nur in sehr geringer Stückzahl verkauft, vielleicht ein bis zweihundert.
• Einige Bücher werden in moderater Auflage verkauft, in Tausenden.
• Nur wenige Bestseller werden in mehr als einer Million Exemplaren verkauft.

Angenommen, Sie trainieren ein lineares Modell, um die Beziehung zwischen Buchcovern und Buchverkäufen zu ermitteln. Bei der datengetriebenen Modellierung mit Rohdaten müsste ein lineares Modell etwas über Buchcover von Büchern finden, die eine Million Mal verkauft werden, das 10.000-mal leistungsfähiger ist als Buchcover von Büchern, die nur 100 Mal verkauft werden. Durch die Logarithmenskala aller Verkaufszahlen wird die Aufgabe jedoch wesentlich einfacher. Beispiel: Der Logarithmus von 100 ist:

  ~4.6 = ln(100)

Das Log von 1.000.000 ist:

  ~13.8 = ln(1,000,000)

Das Logarithmus von 1.000.000 ist also nur etwa dreimal größer als das Logarithmus von 100. Sie können sich wahrscheinlich vorstellen, dass das Cover eines Bestsellers in gewisser Weise etwa dreimal wirkungsvoller ist als das Cover eines Buches, das nur wenige Verkäufe erzielt.

Clipping

Ausbrüche sind ein Verfahren, mit dem der Einfluss extremer Ausreißer minimiert wird. Kurz gesagt: Beim Abrundungsverfahren wird der Wert von Ausreißern in der Regel auf einen bestimmten Maximalwert begrenzt (reduziert). Das Zuschneiden ist eine merkwürdige Idee, kann aber sehr effektiv sein.

Angenommen, ein Dataset enthält ein Merkmal namens roomsPerPerson, das die Anzahl der Zimmer (Gesamtzahl der Zimmer geteilt durch die Anzahl der Personen) für verschiedene Häuser darstellt. Das folgende Diagramm zeigt, dass über 99% der Merkmalswerte einer Normalverteilung entsprechen (ungefähr mit einem Mittelwert von 1,8 und einer Standardabweichung von 0,7). Die Funktion enthält jedoch einige Ausreißer, von denen einige extrem sind:

Abbildung 7: Im Großen und Ganzen normal, aber nicht ganz normal.

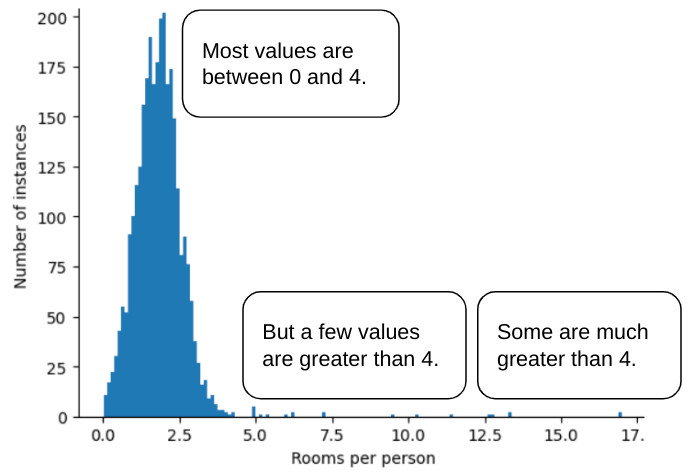
Wie können Sie den Einfluss dieser extremen Ausreißer minimieren? Das Histogramm ist keine gleichmäßige Verteilung, keine Normalverteilung und keine Potenzverteilung. Was ist, wenn Sie den Höchstwert von roomsPerPerson einfach auf einen beliebigen Wert begrenzen, z. B. 4,0?

Abbildung 8: Featurewerte werden bei 4,0 abgeschnitten.

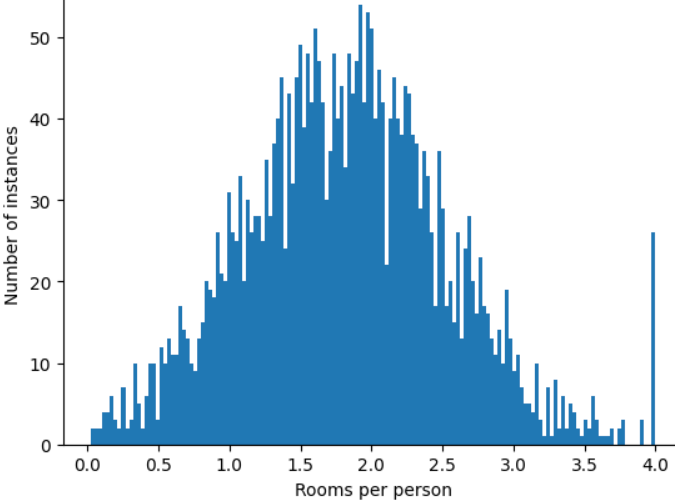
Wenn Sie den Feature-Wert auf 4,0 begrenzen, bedeutet das nicht, dass Ihr Modell alle Werte über 4,0 ignoriert. Vielmehr bedeutet es, dass alle Werte, die über 4,0 lagen, jetzt auf 4,0 gesetzt werden. Das erklärt den merkwürdigen Hügel bei 4,0. Trotz dieses Hügels ist der skalierte Funktionssatz jetzt nützlicher als die ursprünglichen Daten.

Einen Moment! Können Sie wirklich jeden Ausreißerwert auf einen beliebigen oberen Grenzwert reduzieren? Ja, beim Trainieren eines Modells.

Sie können Werte auch zuschneiden, nachdem Sie andere Formen der Normalisierung angewendet haben. Angenommen, Sie verwenden die Z-Score-Skalierung, aber einige Ausreißer haben absolute Werte, die weit über 3 liegen. In diesem Fall haben Sie folgende Möglichkeiten:

• Z-Werte, die größer als 3 sind, werden auf genau 3 gekürzt.
• Z-Werte unter -3 werden auf -3 gekürzt.

Durch das Zuschneiden wird verhindert, dass Ihr Modell unwichtige Daten überindexiert. Einige Ausreißer sind jedoch tatsächlich wichtig. Achten Sie also darauf, die Werte mit Bedacht zu kürzen.

Zusammenfassung der Normalisierungstechniken

Die beste Normalisierungstechnik ist die, die in der Praxis gut funktioniert. Probieren Sie also neue Ideen aus, wenn Sie der Meinung sind, dass sie für Ihre Feature-Verteilung gut geeignet sind.

Normalisierungstechnik	Formel	Anwendung
Lineare Skalierung	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	Wenn das Element gleichmäßig über einen festen Bereich verteilt ist.
Z-Score-Skalierung	$$ x' = \frac{x - μ}{σ}$$	Wenn die Merkmalsverteilung keine extremen Ausreißer enthält.
Logarithmische Skalierung	$$ x' = log(x)$$	Wenn die Funktion dem Potenzgesetz entspricht.
Clipping	Wenn $x > max$, setzen Sie $x' = max$. Wenn $x < min$, setzen Sie $x' = min$.	Wenn das Feature extreme Ausreißer enthält.

Übung: Wissen testen

Welche Methode eignet sich am besten für die Normalisierung eines Merkmals mit der folgenden Verteilung?

Z-Score-Skalierung

Die Datenpunkte folgen im Allgemeinen einer Normalverteilung. Bei der Z-Score-Skalierung werden sie daher in den Bereich von −3 bis +3 gezwungen.

Lineare Skalierung

Lesen Sie die Informationen zu den Normalisierungstechniken auf dieser Seite und versuchen Sie es noch einmal.

Logarithmische Skalierung

Lesen Sie die Informationen zu den Normalisierungstechniken auf dieser Seite und versuchen Sie es noch einmal.

Clipping

Lesen Sie die Informationen zu den Normalisierungstechniken auf dieser Seite und versuchen Sie es noch einmal.

Angenommen, Sie entwickeln ein Modell, mit dem die Produktivität eines Rechenzentrums anhand der im Rechenzentrum gemessenen Temperatur vorhergesagt wird. Fast alle temperature-Werte in Ihrem Datensatz liegen zwischen 15 und 30 °C, mit folgenden Ausnahmen:

• Ein- bis zweimal pro Jahr, an extrem heißen Tagen, werden in temperature einige Werte zwischen 31 und 45 erfasst.
• Jeder 1.000. Punkt in temperature ist auf 1.000 anstelle der tatsächlichen Temperatur festgelegt.

Welches wäre eine angemessene Normalisierungstechnik für temperature?

Ausreißerwerte zwischen 31 und 45 zuschneiden, aber Ausreißer mit dem Wert 1.000 löschen

Die Werte „1.000“ sind Fehler und sollten gelöscht und nicht gekürzt werden.

Die Werte zwischen 31 und 45 sind gültige Datenpunkte. Für diese Werte wäre es wahrscheinlich sinnvoll, die Werte zu begrenzen, vorausgesetzt, der Datensatz enthält nicht genügend Beispiele in diesem Temperaturbereich, um das Modell so zu trainieren, dass es gute Vorhersagen treffen kann. Beachten Sie jedoch, dass das gekippte Modell bei der Inferenz für eine Temperatur von 45 °C dieselbe Vorhersage wie für eine Temperatur von 35 °C trifft.

Alle Ausreißer zuschneiden

Lesen Sie die Informationen zu den Normalisierungstechniken auf dieser Seite und versuchen Sie es noch einmal.

Alle Ausreißer löschen

Lesen Sie die Informationen zu den Normalisierungstechniken auf dieser Seite und versuchen Sie es noch einmal.

Löschen Sie die Ausreißerwerte zwischen 31 und 45, aber beschneiden Sie die Ausreißer mit einem Wert von 1.000.

Lesen Sie die Informationen zu den Normalisierungstechniken auf dieser Seite und versuchen Sie es noch einmal.

Wichtige Begriffe:

• Zuschneiden
• NaN-Trap
• Normalisierung
• Skalieren
• Z-Transformation