O agrupamento por classes (também chamado de agrupamento por classes) é uma
engenharia de atributos
técnica que agrupa diferentes subintervalos numéricos em classes ou
buckets.
Em muitos casos, o agrupamento por classes transforma dados numéricos em dados categóricos.
Por exemplo, considere um recurso
chamado X, cujo menor valor é 15 e
o valor mais alto é 425. Ao usar o agrupamento por classes, é possível representar X com o
cinco agrupamentos a seguir:
- Agrupamento 1: 15 a 34
- Agrupamento 2: 35 a 117
- Agrupamento 3: 118 a 279
- Agrupamento 4: 280 a 392
- Agrupamento 5: 393 a 425
O agrupamento 1 abrange o intervalo de 15 a 34, portanto, todo valor de X entre 15 e 34
acaba na Agrupamento 1. Um modelo treinado nesses agrupamentos não reagirá da mesma forma
a valores X de 17 e 29, já que ambos estão no Agrupamento 1.
O vetor de recurso representa os cinco agrupamentos da seguinte forma:
| Número do agrupamento | Intervalo | Vetor do atributo |
|---|---|---|
| 1 | 15-34 | [1,0, 0,0, 0,0, 0,0, 0,0] |
| 2 | 35-117 | [0,0, 1,0, 0,0, 0,0, 0,0] |
| 3 | 118-279 | [0,0, 0,0, 1,0, 0,0, 0,0] |
| 4 | 280-392 | [0,0, 0,0, 0,0, 1,0, 0,0] |
| 5 | 393-425 | [0,0, 0,0, 0,0, 0,0, 1,0] |
Mesmo que X seja uma única coluna no conjunto de dados, o agrupamento por classes faz com que um modelo
para tratar X como cinco recursos diferentes. Assim, o modelo aprende
pesos separados para cada agrupamento.
O agrupamento por classes é uma boa alternativa ao escalonamento ou recorte quando um dos as seguintes condições sejam atendidas:
- A relação linear geral entre o atributo e o O rótulo é fraco ou inexistente.
- Quando os valores dos atributos são agrupados.
O agrupamento por classes pode parecer contraintuitivo, já que o modelo da exemplo anterior trata os valores 37 e 115 de maneira idêntica. Mas quando um recurso parece mais desajeitado do que o linear, o agrupamento por classes é uma maneira muito melhor de representam os dados.
Exemplo de agrupamento por classes: número de compradores versus temperatura
Suponha que você esteja criando um modelo que prevê o número de compradores pela temperatura externa naquele dia. Aqui está um gráfico temperatura em comparação com o número de compradores:
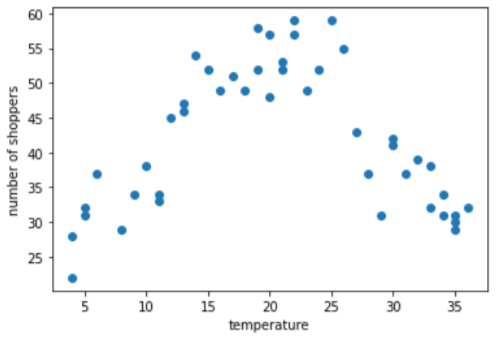
O gráfico mostra, sem surpresa, que o número de compradores foi maior quando e a temperatura era mais confortável.
Você pode representar o atributo como valores brutos: uma temperatura de 35,0 no no conjunto de dados seria 35,0 no vetor de atributo. Essa é a melhor ideia?
No treinamento, um modelo de regressão linear aprende um peso para cada . Portanto, se a temperatura for representada como um único atributo, temperatura de 35,0 teria uma influência cinco vezes maior (ou um quinto da influência) em uma previsão como uma temperatura de 7,0. No entanto, o gráfico não mostram qualquer tipo de relação linear entre o rótulo e o valor do atributo.
O gráfico sugere três clusters nos seguintes subintervalos:
- O agrupamento 1 é a faixa de temperatura de 4 a 11.
- O agrupamento 2 é o intervalo de temperatura de 12 a 26.
- O agrupamento 3 é o intervalo de temperatura de 27 a 36.

O modelo aprende pesos separados para cada agrupamento.
Embora seja possível criar mais de três agrupamentos, até mesmo um agrupamento separado para cada leitura de temperatura, essa não é uma boa ideia pelas seguintes razões:
- Um modelo só pode aprender a associação entre um agrupamento e um rótulo se houver há exemplos suficientes nesse agrupamento. No exemplo dado, cada um dos três agrupamentos contém pelo menos 10 exemplos, o que pode ser suficiente para o treinamento. Com 33 agrupamentos separados, nenhum dos agrupamentos conteria exemplos suficientes para o treinamento do modelo.
- Um compartimento separado para cada temperatura resulta em 33 recursos de temperatura separados. No entanto, você normalmente deve minimizar o número de atributos em um modelo.
Exercício: testar seu conhecimento
O gráfico a seguir mostra o preço médio residencial para cada 0,2 grau de latitude do país mítico da Freedonia:
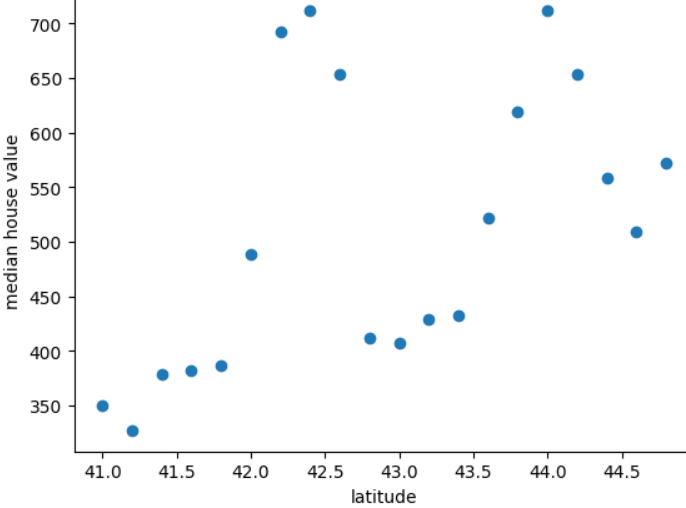
O gráfico mostra um padrão não linear entre o valor inicial e a latitude, portanto, representar a latitude como seu valor de ponto flutuante provavelmente não ajudará de um modelo fazer boas previsões. Talvez o agrupamento por classes de latitude seja uma opção ideia?
- 41,0 a 41,8
- 42,0 a 42,6
- 42,8 a 43,4
- 43,6 a 44,8
Agrupamento por classes quantil
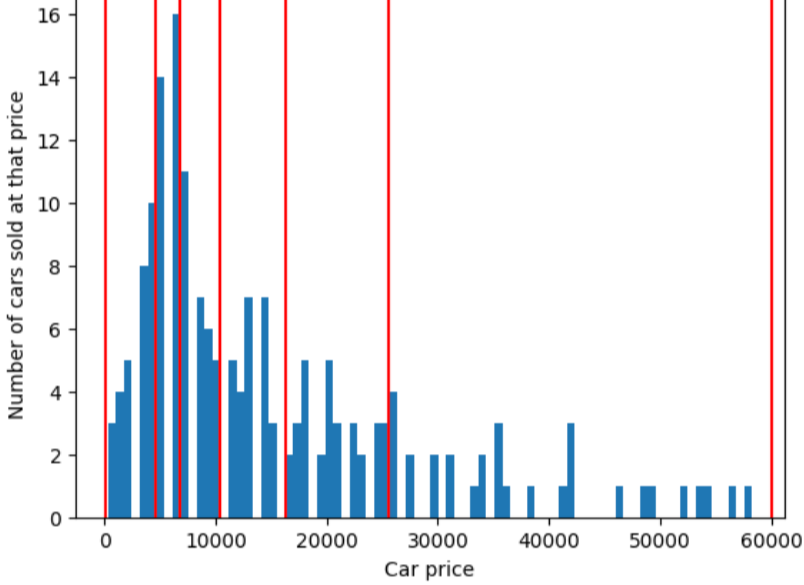
O agrupamento por classes de quantil cria limites de agrupamento, de modo que o número de exemplos em cada bucket é exatamente ou quase igual. Agrupamento por classes de quantis na maioria das vezes oculta os outliers.
Para ilustrar o problema que o agrupamento por classes de quantil resolve, considere o de buckets igualmente espaçados mostrados na figura a seguir, em que dos dez buckets representa um período de exatamente 10.000 dólares. O bucket de 0 a 10.000 contém dezenas de exemplos mas o bucket de 50.000 a 60.000 contém apenas 5 exemplos. Consequentemente, o modelo tem exemplos suficientes para ser treinado nos 0 a 10.000 mas não há exemplos suficientes para treinar para o bucket de 50.000 a 60.000.
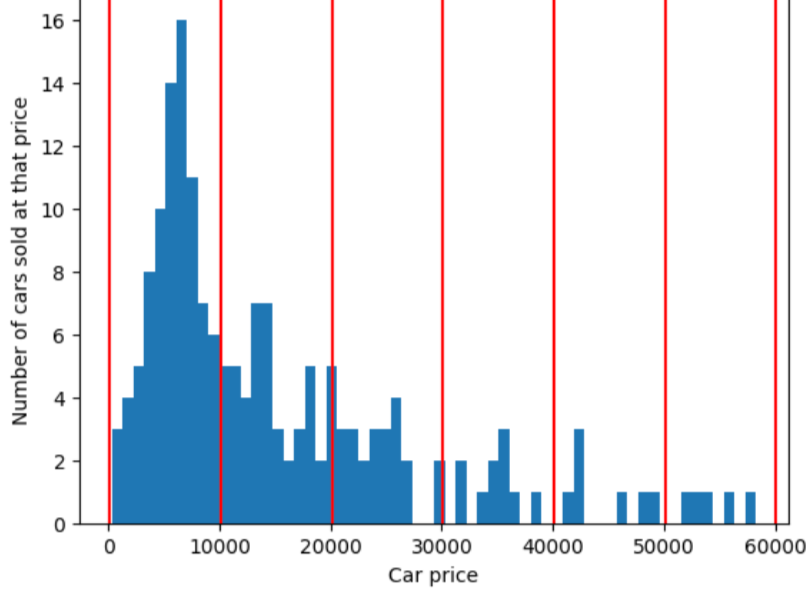
Em contraste, a figura a seguir usa o agrupamento por classes de quantis para dividir os preços dos carros em agrupamentos com aproximadamente o mesmo número de exemplos em cada um deles. Alguns dos agrupamentos têm uma faixa de preço estreita, enquanto outros abrangem uma faixa de preços muito ampla.