Depois de examinar seus dados usando técnicas estatísticas e de visualização, transforme-os de maneiras que ajudem a treinar o modelo de maneira mais eficaz. O objetivo da normalização é transformar atributos estejam em uma escala semelhante. Por exemplo, considere os dois exemplos a seguir recursos:
- O recurso
Xabrange o intervalo de 154 a 24.917.482. - O recurso
Yabrange o intervalo de 5 a 22.
Esses dois atributos abrangem períodos muito diferentes. A normalização pode manipular
X e Y para que eles tenham um intervalo semelhante, talvez de 0 a 1.
A normalização oferece os seguintes benefícios:
- Ajuda os modelos a convergir mais rapidamente durante o treinamento. Quando atributos diferentes têm intervalos distintos, o gradiente descendente pode "rejeitar" e convergência lenta. No entanto, otimizadores mais avançados, como Adagrad e Adam, protegem contra esse problema mudando a taxa de aprendizado efetiva ao longo do tempo.
- Ajuda os modelos a inferir previsões melhores. Quando recursos diferentes têm intervalos diferentes, o modelo resultante pode fazer previsões menos úteis.
- Ajuda a evitar a armadilha do NaN quando os valores do elemento são muito altos.
NaN é uma abreviação de
not a number (número inválido). Quando um valor em um modelo excede
limite de precisão de ponto flutuante, o sistema definirá o valor como
NaNde um número. Quando um número no modelo se torna um NaN, outros números no modelo também se tornam um NaN. - Ajuda o modelo a aprender pesos adequados para cada atributo. Sem o escalonamento de atributos, o modelo presta muita atenção para atributos com ampla amplitude e sem atenção suficiente para atributos intervalos estreitos.
Recomendamos a normalização de recursos numéricos que abrangem intervalos distintos (por exemplo, idade e renda).
Também recomendamos normalizar um único elemento numérico que abranja uma ampla faixa, como city population.
Considere os dois recursos a seguir:
- O menor valor do elemento
Aé -0,5 e o maior é +0,5. - O valor mais baixo do recurso
Bé -5,0, e o mais alto é +5,0.
Os recursos A e B têm extensões relativamente estreitas. No entanto, o período do recurso B é 10 vezes maior que o do recurso A. Assim:
- No início do treinamento, o modelo presume que o atributo
Aé dez vezes mais "importante" do que o atributoB. - O treinamento levará mais tempo do que deveria.
- O modelo resultante pode não ser o ideal.
O dano geral causado pela não normalização será relativamente pequeno; No entanto, recomendamos normalizar os atributos A e B na mesma escala, talvez de -1,0 a +1,0.
Agora, considere dois recursos com uma maior disparidade de intervalos:
- O valor mais baixo do recurso
Cé -1, e o mais alto é +1. - O menor valor do atributo
Dé +5.000, e o maior é +1.000.000.000.
Se você não normalizar os atributos C e D, o modelo provavelmente vai
ficar abaixo do ideal. Além disso, o treinamento levará muito mais tempo para
convergir ou até mesmo não convergir totalmente.
Esta seção aborda três métodos conhecidos de normalização:
- escalonamento linear
- Escala Z-score
- dimensionamento logarítmico
Esta seção também aborda cortes. Embora não seja um verdadeiro de normalização, o recorte doma atributos numéricos desordenados em que produzem modelos melhores.
Dimensionamento linear
Escalonamento linear (mais comumente encurtado para apenas escalonamento) significa converter valores de ponto flutuante de o intervalo natural em um intervalo padrão, geralmente de 0 a 1 ou -1 a +1.
O escalonamento linear é uma boa opção quando todas as condições a seguir são atendidas:
- Os limites inferior e superior dos dados não mudam muito com o tempo.
- O recurso tem poucos ou nenhum valor fora da curva, e esses valores não são extremos.
- O recurso é distribuído de forma aproximadamente uniforme em todo o intervalo. Ou seja, um histograma mostraria barras aproximadamente uniformes para a maioria dos valores.
Suponha que o age humano seja um recurso. O escalonamento linear é uma boa normalização
técnica para age porque:
- Os limites inferior e superior aproximados são de 0 a 100.
agecontém uma porcentagem relativamente pequena de valores discrepantes. Apenas cerca de 0,3% da população tem mais de 100 anos.- Embora certas idades sejam um pouco melhor representadas do que outras, uma grande deve conter exemplos suficientes de todas as idades.
Exercício: testar seu conhecimento
Suponha que seu modelo tenha um atributo chamadonet_worth que contém a rede
valor de pessoas diferentes. O escalonamento linear seria uma boa normalização
técnica para net_worth? Por que sim ou por que não?
Escalonamento do escore padronizado
Um valor Z é o número de desvios padrão de um valor em relação à média. Por exemplo, um valor maior que a média de duas vezes o desvio padrão tem um Z-score de +2,0. Um valor menor que 1,5 desvios padrão do que a média tem um valor Z de -1,5.
Representar um atributo com dimensionamento de Z-score significa armazenar o Z-score desse atributo no vetor de atributo. Por exemplo, a figura a seguir mostra duas histogramas:
- À esquerda, uma distribuição normal clássica.
- À direita, a mesma distribuição normalizada pelo escalonamento da pontuação Z.
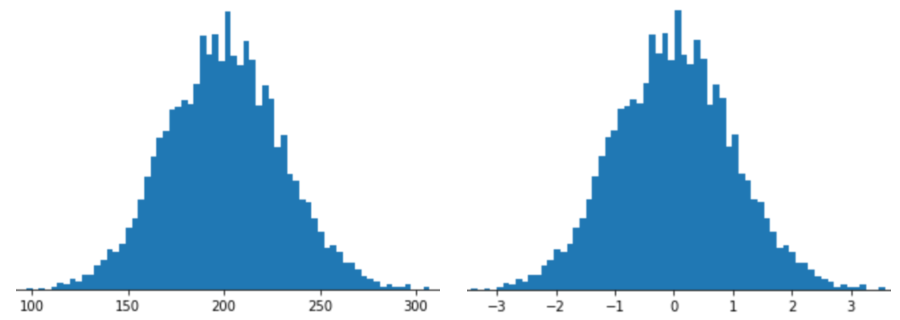
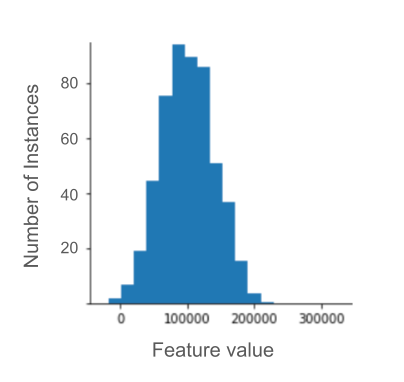
A escala de Z-score também é uma boa escolha para dados como os mostrados na figura a seguir, que tem apenas uma distribuição vagamente normal.
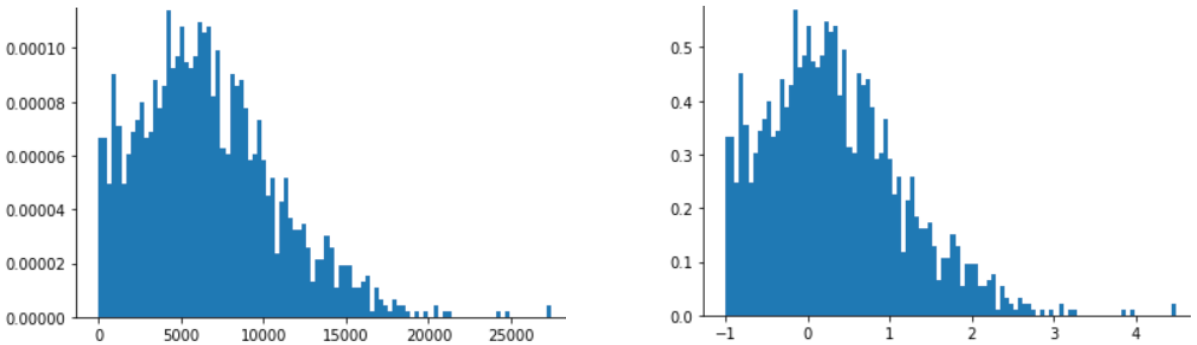
O z-score é uma boa opção quando os dados seguem uma distribuição normal ou uma distribuição semelhante a uma distribuição normal.
Algumas distribuições podem ser normais na maior parte
mas ainda contêm outliers extremos. Por exemplo, quase todos
em um atributo net_worth podem se encaixar perfeitamente em três desvios padrão:
mas alguns exemplos desse atributo podem ser centenas de desvios padrão
da média. Nessas situações, você pode combinar o escalonamento do valor Z com
outra forma de normalização (geralmente recorte) para lidar com essa situação.
Exercício: testar seu conhecimento
Suponha que seu modelo treine em um atributo chamadoheight que contenha o adulto.
de 10 milhões de mulheres. A escala Z seria uma boa normalização?
técnica para height? Por que sim ou por que não?
Dimensionamento logarítmico
A escala logarítmica calcula o logaritmo do valor bruto. Em teoria, o logaritmo pode ser qualquer base. Na prática, a escala logarítmica geralmente calcula o logaritmo natural (ln).
O escalonamento de registros é útil quando os dados estão em conformidade com uma distribuição da lei de potência. Informalmente, uma distribuição de lei de potência é assim:
- Valores baixos de
Xtêm valores muito altos deY. - À medida que os valores de
Xaumentam, os valores deYdiminuem rapidamente. Consequentemente, valores altos deXtêm valores muito baixos deY.
As classificações de filmes são um bom exemplo de distribuição da lei de poder. Nos seguintes Observe o seguinte:
- Alguns filmes têm muitas avaliações de usuários. Valores baixos de
Xtêm valores altos deY. - A maioria dos filmes tem poucas classificações dos usuários. Os valores altos de
Xtêm valores baixos deY.
A escala logarítmica muda a distribuição, o que ajuda a treinar um modelo que fará previsões melhores.
Como segundo exemplo, as vendas de livros se conformam a uma distribuição de lei de potência porque:
- A maioria dos livros publicados vende um número muito pequeno de cópias, talvez uma ou duas centenas.
- Alguns livros vendem um número moderado de cópias, aos milhares.
- Apenas alguns mais vendidos venderão mais de um milhão de cópias.
Suponha que você esteja treinando um modelo linear para encontrar a relação como capas de livros para vendas de livros. Um treinamento de modelo linear com valores brutos preciso encontrar algo sobre as capas dos livros que vendem um milhão de cópias que é 10.000 mais poderosa do que capas de livros que vendem apenas 100 cópias. No entanto, a escalação de registro de todos os valores de vendas torna a tarefa muito mais viável. Por exemplo, o registro de 100 é:
~4.6 = ln(100)
enquanto o registro de 1.000.000 é:
~13.8 = ln(1,000,000)
Portanto, o registro de 1.000.000 é apenas cerca de três vezes maior do que o registro de 100. Você provavelmente poderia imaginar que a capa de um livro mais vendido é cerca de três vezes mais poderosa (de alguma forma) do que a capa de um livro que vende pouco.
Corte
Recorte é uma técnica para minimizar a influência de outliers extremos. Em resumo, o truncamento geralmente limita (reduz) o valor de valores discrepantes para um valor máximo específico. O recorte é uma ideia estranha, mas pode ser muito eficaz.
Por exemplo, imagine um conjunto de dados com um recurso chamado roomsPerPerson,
que representa o número de cômodos (total de cômodos dividido
pelo número de ocupantes) de várias casas. O gráfico a seguir mostra que mais de 99% dos valores de atributos estão em conformidade com uma distribuição normal (aproximadamente uma média de 1,8 e um desvio padrão de 0,7). No entanto, o recurso contém
alguns valores atípicos, alguns extremos:
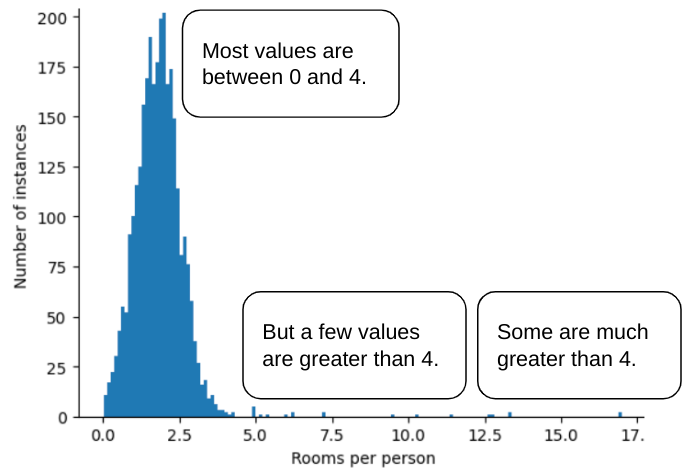
Como minimizar a influência desses outliers extremos? Bem, o
histograma não é uma distribuição uniforme, uma distribuição normal ou uma lei de potência
e distribuição de dados. E se você simplesmente limitar ou recortar o valor máximo
roomsPerPerson a um valor arbitrário, por exemplo, 4.0?
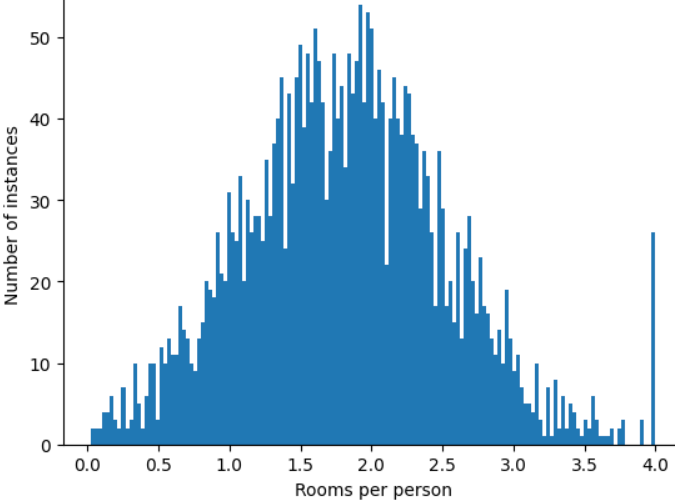
Cortar o valor do atributo em 4.0 não significa que o modelo ignora todas valores maiores que 4,0. Em vez disso, significa que todos os valores maiores que 4,0 agora se tornam 4,0. Isso explica a peculiar colina da 4.0. Apesar disso, o conjunto de recursos dimensionado agora é mais útil do que os dados originais.
Espere um momento! É possível reduzir todos os valores discrepantes para um limite superior arbitrário? Ao treinar um modelo, sim.
Também é possível cortar valores depois de aplicar outras formas de normalização. Por exemplo, suponha que você use a escala de Z-score, mas alguns valores discrepantes tenham valores absolutos muito maiores que 3. Nesse caso, você pode:
- Corte os valores Z maiores do que 3 para se tornar exatamente 3.
- Os escores Z menores que -3 são cortados para se tornarem exatamente -3.
O recorte impede que o modelo indexe demais dados sem importância. No entanto, alguns valores atípicos são importantes, então corte os valores com cuidado.
Resumo das técnicas de normalização
| Técnica de normalização | Fórmula | Quando usar |
|---|---|---|
| Dimensionamento linear | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | Quando o elemento é distribuído uniformemente em um intervalo fixo. |
| Escalonamento do escore padronizado | $$ x' = \frac{x - μ}{σ}$$ | Quando a distribuição de recursos não contém valores extremos. |
| Dimensionamento logarítmico | $$ x' = log(x)$$ | Quando o recurso está em conformidade com a lei de potência. |
| Recorte | Se $x > max$, definir $x' = máx. US$ Se $x < min$, definir $x' = mín. de$ |
Quando o atributo contém outliers extremos. |
Exercício: teste seus conhecimentos
Suponha que você esteja desenvolvendo um modelo que prevê a produtividade de um data center com base na temperatura medida dentro dele.
Quase todos os valores de temperature no conjunto de dados estão entre 15 e 30 (Celsius), com as seguintes exceções:
- Uma ou duas vezes por ano, em dias extremamente quentes, alguns valores entre
31 e 45 são registrados em
temperature. - Cada milésimo ponto em
temperatureé definido como 1.000, em vez da temperatura real.
Essa seria uma técnica de normalização razoável para
temperature?
Os valores de 1.000 são erros e devem ser excluídos cortada.
Os valores entre 31 e 45 são pontos de dados legítimos. O recorte seria uma boa ideia para esses valores, supondo que o conjunto de dados não contém exemplos suficientes treinar o modelo para fazer boas previsões. No entanto, durante a inferência, note que o modelo recortado faria a mesma previsão para uma temperatura de 45 para uma temperatura de 35.