La agrupación (también llamada agrupamiento) es un
ingeniería de atributos
técnica que agrupa diferentes subrangos numéricos en discretizaciones o
buckets.
En muchos casos, la discretización convierte datos numéricos en datos categóricos.
Por ejemplo, considera un atributo
llamado X cuyo valor más bajo es 15 y
el valor más alto es 425. Con la discretización, podrías representar X con el
siguientes cinco discretizaciones:
- Bandeja 1: 15 a 34
- Bandeja 2: 35 a 117
- Bandeja 3: 118 a 279
- Bandeja 4: 280 a 392
- Bandeja 5: 393 a 425
La discretización 1 abarca el rango de 15 a 34, por lo que cada valor de X se extiende entre 15 y 34.
termina en la bandeja 1. Un modelo entrenado con estos discretizaciones no reaccionará de manera diferente
a valores X de 17 y 29, ya que ambos valores están en la bandeja 1.
El vector de atributos representa las cinco discretizaciones de la siguiente manera:
| Número de bandeja | Rango | Vector de atributos |
|---|---|---|
| 1 | 15-34 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35-117 | [0.0, 1.0, 0.0, 0.0, 0.0] |
| 3 | 118-279 | [0.0, 0.0, 1.0, 0.0, 0.0] |
| 4 | 280-392 | [0.0, 0.0, 0.0, 1.0, 0.0] |
| 5 | 393-425 | [0.0, 0.0, 0.0, 0.0, 1.0] |
Aunque X es una sola columna en el conjunto de datos, la discretización causa un modelo
para tratar a X como cinco atributos independientes. Por lo tanto, el modelo aprende
pesos separados para cada discretización.
La discretización es una buena alternativa al escalamiento o recorte cuando cualquiera de los se cumplen las siguientes condiciones:
- La relación lineal general entre el atributo y el label es débil o inexistente.
- Cuando los valores de los atributos se agrupan en clústeres.
La discretización puede parecer contradictoria, dado que el modelo del el ejemplo anterior trata los valores 37 y 115 de manera idéntica. Pero cuando un atributo parece más torpe que el lineal, la discretización es una manera mucho mejor de representan los datos.
Ejemplo de discretización: cantidad de compradores frente a temperatura
Supongamos que creas un modelo que predice la cantidad de compradores por la temperatura exterior de ese día. Aquí hay un diagrama temperatura frente a la cantidad de compradores:

El gráfico muestra, como es lógico, que la cantidad de compradores fue mayor cuando la temperatura era la más cómoda.
Podrías representar el atributo como valores sin procesar: una temperatura de 35.0 en el sería 35.0 en el vector de atributos. ¿Es esa la mejor idea?
Durante el entrenamiento, un modelo de regresión lineal aprende un solo peso para cada . Por lo tanto, si la temperatura se representa como una única función, un temperatura de 35.0 tendría cinco veces la influencia (o un quinto influencia) en una predicción como una temperatura de 7.0. Sin embargo, el diagrama no mostrar algún tipo de relación lineal en el valor del atributo.
El gráfico sugiere tres clústeres en los siguientes subrangos:
- La discretización 1 es el rango de temperatura de 4 a 11.
- La discretización 2 es el rango de temperatura de 12 a 26.
- La discretización 3 es el rango de temperatura de 27 a 36.

El modelo aprende pesos separados para cada discretización.
Si bien es posible crear más de tres discretizaciones, incluso una independiente para cada medición de temperatura, esto suele ser una mala idea por las siguientes razones:
- Un modelo solo puede aprender la asociación entre una discretización y una etiqueta si hay hay suficientes ejemplos en esa bandeja. En el ejemplo dado, cada una de las 3 discretizaciones contiene al menos 10 ejemplos, que podrían ser suficientes para el entrenamiento. Con 33 bandejas separadas, ninguna de las discretizaciones contendrá suficientes ejemplos para que el modelo se entrene.
- Un depósito separado para cada temperatura da como resultado 33 funciones de temperatura separadas. Sin embargo, por lo general, debes minimizar la cantidad de atributos en un modelo.
Ejercicio: Comprueba tus conocimientos
El siguiente gráfico muestra la mediana del precio de una casa para cada 0.2 grados de del país mítico de Freedonia:
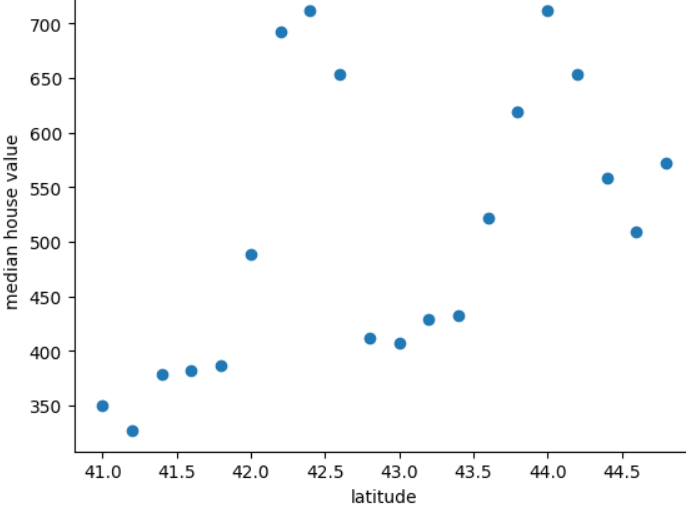
El gráfico muestra un patrón no lineal entre el valor de la casa y la latitud, por lo que es poco probable que representar la latitud como valor de punto flotante ayude que un modelo haga buenas predicciones. Quizás agrupar latitudes sería una mejor idea?
- 41.0 a 41.8
- 42.0 a 42.6
- 42.8 a 43.4
- 43.6 a 44.8
Agrupamiento en cuantiles
El agrupamiento en cuantiles crea límites de agrupamiento, de modo que la cantidad de ejemplos en cada bucket es exacta o casi igual. Agrupamiento en cuantiles principalmente oculta los valores atípicos.
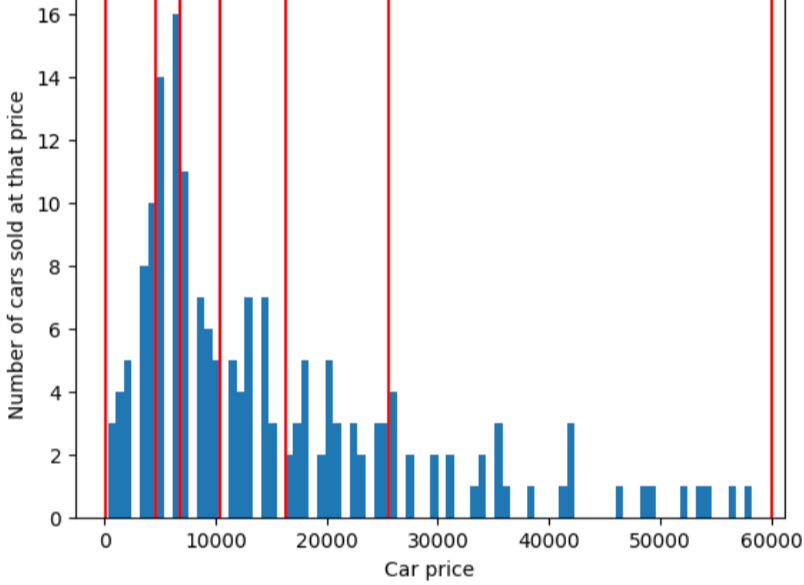
Para ilustrar el problema que resuelve el agrupamiento en cuantiles, considera buckets espaciados igual que se muestra en la siguiente figura, donde cada de los diez buckets representa un intervalo de exactamente 10,000 dólares. Observa que el bucket de 0 a 10,000 contiene decenas de ejemplos pero el bucket de 50,000 a 60,000 contiene solo 5 ejemplos. Por lo tanto, el modelo tiene suficientes ejemplos para entrenar en el rango de 0 a 10,000 pero no hay suficientes ejemplos para entrenar en el bucket de 50,000 a 60,000.
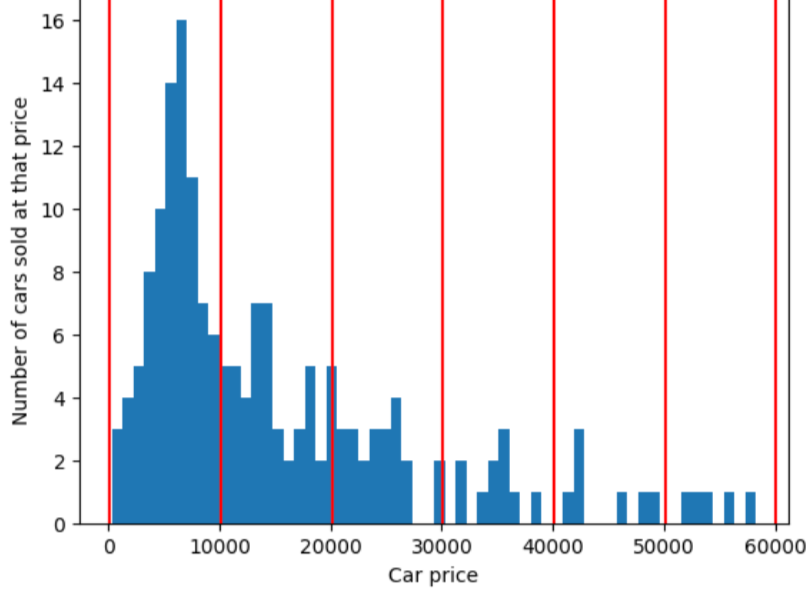
En cambio, la siguiente figura utiliza el agrupamiento en cuantiles para dividir los precios de los automóviles en discretizaciones con aproximadamente la misma cantidad de ejemplos en cada intervalo. Ten en cuenta que algunas discretizaciones abarcan un intervalo de precios limitado, mientras que otras abarcan un intervalo de precios muy amplio.