Después de examinar tus datos con técnicas estadísticas y de visualización, debes transformarlos de manera que ayuden a que tu modelo se entrene de manera más eficaz. El objetivo de normalization es transformar para que los atributos estén en una escala similar. Por ejemplo, considera las siguientes dos funciones:
- El atributo
Xabarca el rango de 154 a 24,917,482. - El atributo
Yabarca el rango de 5 a 22.
Estas dos funciones abarcan rangos muy diferentes. La normalización puede manipular
X y Y para que abarquen un rango similar, quizás de 0 a 1.
La normalización proporciona los siguientes beneficios:
- Ayuda a los modelos a converger más rápido durante el entrenamiento. Cuando diferentes atributos tienen diferentes rangos, el descenso por gradiente puede “rebotar” y ralentizar la convergencia. Dicho esto, los optimizadores más avanzados, como Adagrad y Adam lo protegen contra este problema y cambian la tasa de aprendizaje eficaz con el tiempo.
- Ayuda a los modelos a inferir mejores predicciones. Cuando diferentes atributos tienen distintos rangos, el resultado modelo podría hacer predicciones menos útiles.
- Ayuda a evitar la "trampa de NaN" cuando los valores de los atributos son muy altos.
NaN es la sigla en inglés de not a number. Cuando un valor en un modelo supera el
límite de precisión de punto flotante, el sistema establece el valor en
NaNen su lugar de un número. Cuando un número en el modelo se convierte en NaN, otros números en el modelo finalmente se convierte en un NaN. - Ayuda al modelo a aprender los pesos adecuados para cada atributo. Sin el escalamiento de atributos, el modelo presta demasiada atención a funciones con rangos amplios y no hay suficiente atención a las los rangos estrechos.
Recomendamos normalizar los atributos numéricos que abarcan rangos claramente diferentes (por ejemplo, edad e ingresos).
También recomendamos que se normalice un solo atributo numérico que cubra un rango amplio, como city population..
Considera las siguientes dos funciones:
- El valor más bajo del atributo
Aes -0.5 y el más alto es +0.5. - El valor más bajo del atributo
Bes -5.0 y el más alto, +5.0.
Los atributos A y B tienen intervalos relativamente estrechos. Sin embargo, la función B
es 10 veces más ancho que el intervalo del atributo A. Por lo tanto:
- Al comienzo del entrenamiento, el modelo supone que el atributo
Aes diez veces más “importante” que el atributoB. - El entrenamiento tardará más de lo debido.
- Es posible que el modelo resultante no sea el óptimo.
El daño general por no realizar la normalización será relativamente pequeño. Sin embargo, te recomendamos que normalices las funciones A y B en la misma escala, quizás de -1.0 a +1.0.
Ahora, considera dos atributos con una mayor disparidad de rangos:
- El valor más bajo de la función
Ces -1 y el más alto es +1. - El valor más bajo de la función
Des +5,000 y el más alto es +1,000,000,000.
Si no normalizas los atributos C
y D, es probable que tu modelo
ser subóptimo. Además, el entrenamiento llevará mucho más tiempo
o no converjan por completo.
En esta sección, se describen tres métodos de normalización populares:
- escalamiento lineal
- Escalamiento de la puntuación Z
- escalamiento logarítmico
Esta sección también abarca recorte Aunque no es una técnica de normalización real, el recorte controla los atributos numéricos ingobernables en rangos que producen mejores modelos.
Escalamiento lineal
Escalamiento lineal (con mayor frecuencia abreviado a solo escalamiento) significa convertir los valores de punto flotante de su rango natural dentro de un rango estándar, por lo general de 0 a 1, o De -1 a +1.
El escalamiento lineal es una buena opción cuando se cumplen todas las condiciones siguientes:
- Los límites inferior y superior de tus datos no cambian mucho con el tiempo.
- El atributo contiene pocos valores atípicos o ninguno, y esos valores no son extremo.
- El atributo se distribuye de forma aproximadamente uniforme en su rango. Es decir, un histograma mostraría barras aproximadamente iguales para la mayoría de los valores.
Supongamos que el age humano es un atributo. El escalamiento lineal es una buena técnica de normalización para age porque:
- Los límites inferior y superior aproximados son de 0 a 100.
agecontiene un porcentaje relativamente pequeño de valores atípicos. Solo el 0.3% de la población tiene más de 100 años.- Aunque ciertas edades están algo mejor representadas que otras, un conjunto de datos grande debe contener ejemplos suficientes de todas las edades.
Ejercicio: Comprueba tu comprensión
Supongamos que tu modelo tiene un atributo llamadonet_worth que contiene la red
de personas diferentes. ¿El escalamiento lineal sería una buena normalización
técnica para net_worth? ¿Por qué?
Escalamiento de puntuación Z
Una puntuación Z es la cantidad de desviaciones estándar que tiene un valor a partir de la media. Por ejemplo, un valor que es 2 desviaciones estándar mayores que la media tiene una puntuación Z de +2.0. Un valor que es 1.5 desviaciones estándar menos que la media tiene una puntuación Z de -1.5.
Representar un atributo con escalamiento de puntuación Z significa almacenar el atributo Puntuación Z en el vector de atributos Por ejemplo, en la siguiente figura, se muestran dos histogramas:
- A la izquierda, una distribución normal clásica.
- A la derecha, la misma distribución normalizada por escala de puntuación Z.
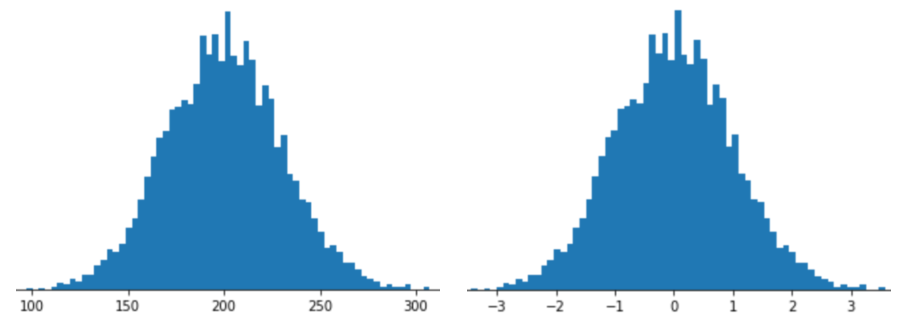
La escala de puntuación Z también es una buena opción para datos como los que se muestran en la siguiente figura, que tiene una distribución vagamente normal.
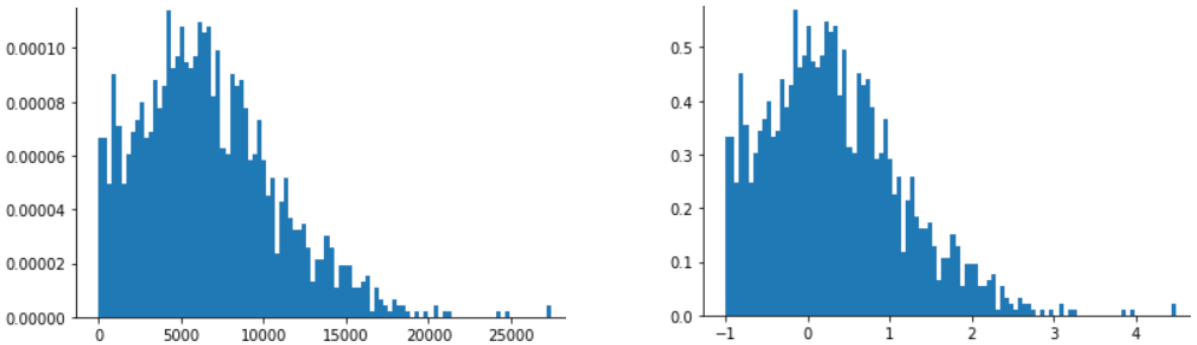
La puntuación z es una buena opción cuando los datos siguen una distribución normal o una distribución, algo similar a una distribución normal.
Ten en cuenta que algunas distribuciones pueden ser normales en la mayor parte de su rango, pero aún contienen valores extremos. Por ejemplo, casi todos los
los puntos de un atributo net_worth pueden encajar perfectamente en 3 desviaciones estándar,
pero algunos ejemplos de esta función
podrían ser cientos de desviaciones estándar
de la media. En estas situaciones, puedes combinar el escalamiento de puntuación Z con
Es otra forma de normalización (por lo general, recorte) para manejar esta situación.
Ejercicio: Comprueba tu comprensión
Supongamos que tu modelo se entrena en un atributo llamadoheight que contiene las alturas de diez millones de mujeres adultas. ¿El escalamiento de puntuación Z sería una buena normalización
técnica para height? ¿Por qué?
Escalamiento logarítmico
La escala de registro calcula el logaritmo del valor sin procesar. En teoría, el logaritmo podría ser cualquier base. En la práctica, la escala de registro suele calcular el logaritmo natural (ln).
La escala de registro es útil cuando los datos se ajustan a una distribución de ley de potencia. De manera casual, una distribución de una ley de poder se ve de la siguiente manera:
- Los valores bajos de
Xtienen valores muy altos deY. - A medida que aumentan los valores de
X, los valores deYdisminuyen rápidamente. En consecuencia, los valores altos deXtienen valores muy bajos deY.
Las calificaciones de las películas son un buen ejemplo de la distribución de una ley de poder. En la siguiente figura, observa lo siguiente:
- Algunas películas tienen muchas calificaciones de usuarios. (Los valores bajos de
Xtienen valores altos deY). - La mayoría de las películas tienen muy pocas calificaciones de los usuarios. (Los valores altos de
Xtienen valores bajos deY).
El escalamiento logarítmico cambia la distribución, lo que ayuda a entrenar un modelo que hacer mejores predicciones.
Como segundo ejemplo, las ventas de libros se ajustan a una distribución de ley de potencia porque:
- La mayoría de los libros publicados venden una pequeña cantidad de copias, quizás una o doscientas.
- Algunos libros venden una cantidad moderada de copias, por miles.
- Solo algunos bestsellers venderán más de un millón de copias.
Supongamos que entrenas un modelo lineal para encontrar la relación por ejemplo, portadas de libros para reservar ventas. Un modelo de entrenamiento lineal en valores sin procesar tendría que encontrar algo sobre las portadas de los libros que venden un millón de copias que sea 10,000 veces más potente que las portadas de los libros que venden solo 100 copias. Sin embargo, el escalamiento logarítmico de todas las cifras de ventas hace que la tarea sea mucho más factible. Por ejemplo, el registro de 100 es:
~4.6 = ln(100)
mientras que el registro de 1,000,000 es:
~13.8 = ln(1,000,000)
Por lo tanto, el logaritmo de 1,000,000 es solo tres veces mayor que el logaritmo de 100. Probablemente podrías imaginar que la portada de un libro de éxitos en ventas es tres veces. más poderosa (de alguna manera) que una portada de libro en venta pequeña.
Recorte
El recorte es una técnica para minimizar la influencia de valores atípicos extremos. En resumen, el recorte suele limitar (reduce) el valor de los valores atípicos a un valor máximo específico. El recorte es una idea extraña y, sin embargo, puede ser muy eficaz.
Por ejemplo, imagina un conjunto de datos que contiene un atributo llamado roomsPerPerson, que representa la cantidad de habitaciones (cantidad total de habitaciones dividida por la cantidad de ocupantes) de varias casas. En el siguiente gráfico, se muestra que más del 99% de los valores de la función se ajustan a una distribución normal (aproximadamente, una media de 1.8 y una desviación estándar de 0.7). Sin embargo, la función contiene
algunos valores atípicos, algunos extremos:
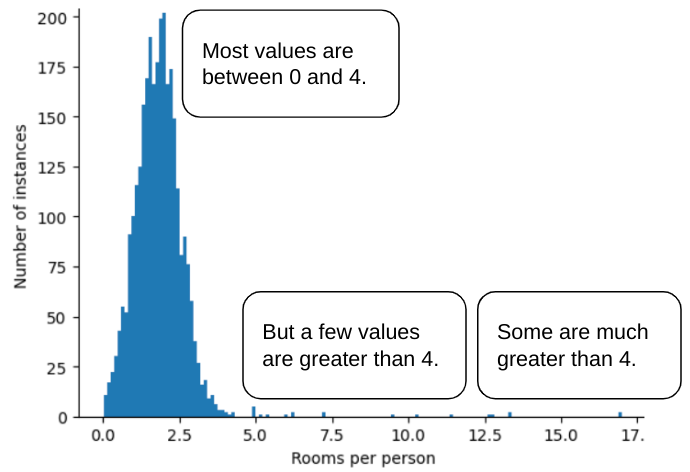
¿Cómo puedes minimizar la influencia de esos valores atípicos extremos? Bueno,
un histograma no es una distribución uniforme, una distribución normal o una ley de potencia
distribución. ¿Qué sucede si simplemente limitas o recortas el valor máximo de roomsPerPerson en un valor arbitrario, por ejemplo, 4.0?
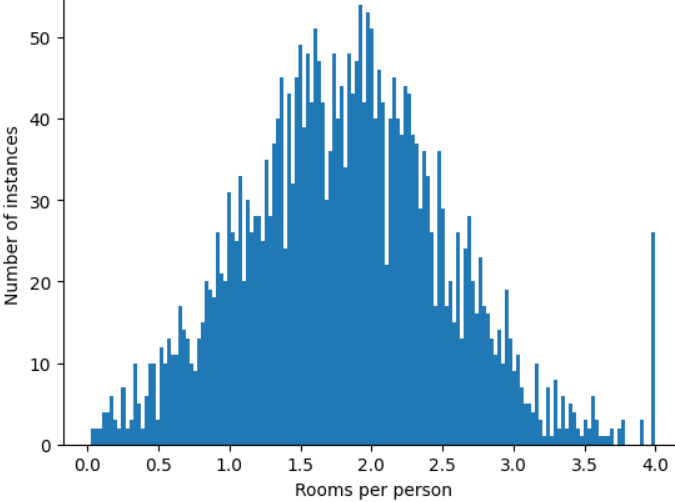
Recortar el valor de la función en 4.0 no significa que tu modelo omita todos los valores superiores a 4.0. En cambio, significa que todos los valores que fueron mayores a 4.0 ahora se convierten en 4.0. Esto explica la colina peculiar en 4.0. A pesar de esa colina, el conjunto de atributos ajustado ahora es más útil que los datos originales.
Espera un momento. ¿Realmente puedes reducir cada valor atípico a un umbral superior arbitrario? Sí, cuando entrenas un modelo.
También puedes recortar valores después de aplicar otras formas de normalización. Por ejemplo, supongamos que utilizas el escalamiento de puntuación Z, pero algunos valores atípicos tienen absolutos mayores que 3. En ese caso, podrías hacer lo siguiente:
- Recortar las puntuaciones Z superiores a 3 para que sean exactamente 3
- Corta las puntuaciones Z inferiores a -3 para que sean exactamente -3.
El recorte evita que tu modelo sobreindexe datos sin importancia. Sin embargo, algunos valores atípicos son importantes, por lo que debes recortar los valores con cuidado.
Resumen de las técnicas de normalización
| Técnica de normalización | Formula | Cuándo debe utilizarse |
|---|---|---|
| Escalamiento lineal | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | Cuando el componente se distribuye de manera uniforme en un rango fijo. |
| Escalamiento de puntuación Z | $$ x' = \frac{x - μ}{σ}$$ | Cuando la distribución de componentes no contiene valores atípicos extremos. |
| Escalamiento logarítmico | $$ x' = log(x)$$ | Cuando el atributo cumple con la ley de potencia. |
| Recorte | Si USD x > max$, establece $x' = máx.$ Si USD x < mín$, establecer $x' = min$ |
Cuando el atributo contiene valores extremos. |
Ejercicio: Pon a prueba tus conocimientos
Supongamos que estás desarrollando un modelo que predice la productividad de un centro de datos según la temperatura medida en su interior.
Casi todos los valores temperature de tu conjunto de datos caen
entre 15 y 30 (Celsius), con las siguientes excepciones:
- Una o dos veces al año, en días extremadamente calurosos, se registran algunos valores entre 31 y 45 en
temperature. - Cada 1,000 puntos en
temperaturese establece en 1,000 en lugar de la temperatura real.
¿Cuál sería una técnica de normalización razonable para
temperature?
Los valores de 1,000 son errores y se deben borrar en lugar de recortado.
Los valores entre 31 y 45 son datos legítimos. Es probable que sea una buena idea recortar estos valores, siempre que el conjunto de datos no contenga suficientes ejemplos en este rango de temperatura para entrenar al modelo y que realice buenas predicciones. Sin embargo, durante la inferencia, ten en cuenta que el modelo recortado haría la misma predicción para una temperatura de 45 grados y una temperatura de 35.