ビニング(バケット化とも呼ばれます)は、
特徴量エンジニアリング
異なる数値サブ範囲をビンまたは
bucket。
多くの場合、ビニングは数値データをカテゴリデータに変換します。
たとえば、対象物について考えてみましょう。
X の最小値が 15 で、
425 になります。ビニングを使用すると、X は次のように表せます。
5 つのビンがあります。
- ビン 1: 15 ~ 34
- ビン 2: 35 ~ 117
- ビン 3: 118 ~ 279
- ビン 4: 280 ~ 392
- ビン 5: 393 ~ 425
ビン 1 は 15 ~ 34 の範囲なので、X のすべての値は 15 ~ 34 です。
最終的にビン 1 に入りますこれらのビンでトレーニングされたモデルは、これまでと変わらない
17 と 29 の両方の値がビン 1 にあるため、X の値になります。
特徴ベクトルは以下を表します。 5 つのビンを分類します。
| ビン番号 | 範囲 | 特徴ベクトル |
|---|---|---|
| 1 | 15 ~ 34 歳 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35 ~ 117 | [0.0、1.0、0.0、0.0、0.0] |
| 3 | 118 ~ 279 | [0.0, 0.0, 1.0, 0.0, 0.0] |
| 4 | 280 ~ 392 | [0.0、0.0、0.0、1.0、0.0] |
| 5 | 393 ~ 425 | [0.0、0.0、0.0、0.0、1.0] |
X はデータセット内の単一の列ですが、ビニングによってモデルが
X を 5 つの独立した特徴として扱います。そのため、このモデルは
各ビンに別々の重みを設定します
ビニングはスケーリングの代替として使用できる クリッピングのいずれかが 次の条件が満たされています。
- 特徴と特徴の間の全体的な線形関係は、 ラベルが弱いか、存在しません。
- 特徴値がクラスタ化される場合。
ビニングのモデルは直感に反するかもしれませんが、 上記の例では、値 37 と 115 を同じように扱います。しかし、 特徴が線形よりもぼやけて見える場合は、ビニングが データを表します
ビニングの例: 買い物客数と温度
100 ミリ秒以内の数を予測するモデルを作成するとします。 予測していますこのグラフは、 買い物客の数に対する

このグラフから、当然のことながら、買い物客の数が最も多かったのが 温度が一番快適だったから。
この場合、この特徴を未加工の値として表現できます。 特徴ベクトルの 35.0 になりますよろしいでしょうか?
線形回帰モデルはトレーニング中に、モデルごとに 説明します。したがって、温度が 1 つの特徴として表される場合、 temperature を 35.0 に設定すると影響は 5 倍(つまり 温度 7.0 として予測を行う場合です。ただし、プロットは ラベルとラベルの間になんらかの直線関係がある 特徴値を取得します。
グラフには、次のサブ範囲の 3 つのクラスタがあります。
- ビン 1 は温度範囲 4 ~ 11 です。
- ビン 2 は温度範囲 12 ~ 26 です。
- ビン 3 は温度範囲 27 ~ 36 です。
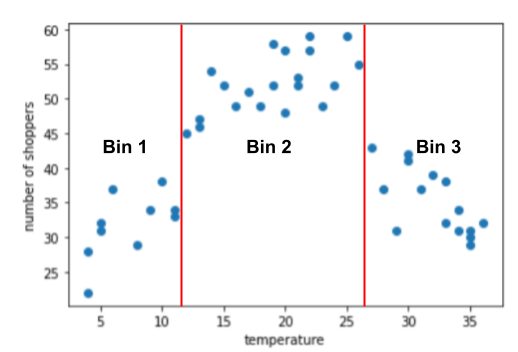
このモデルは、ビンごとに別々の重みを学習します。
3 つ以上のビンを作成することも可能ですが、 次のような理由から、この方法は多くの場合に適切ではありません。
- ビンとラベルの関連付けを学習できるのは、 十分な数の例を確認できます。上の例では、3 つのビンのそれぞれが 少なくとも 10 個のサンプルが含まれているので、トレーニングには十分な可能性があります。 33 個のビンがあり どのビンにもモデルのトレーニングに 十分なサンプルが含まれません
- 温度ごとに別個のビンを作成すると、次のようになります。 33 種類の温度特性。ただし、通常は、広告を最小化し、 モデル内の特徴の数です
演習:理解度をチェックする
次のプロットは、各 0.2 度ごとの住宅価格の中央値を示しています。 神話に登場する国「フリードニア」の緯度:

この図は、住宅の値と緯度の間の非線形パターンを示しています。 そのため、緯度を浮動小数点値で表現してもあまり役に立ちません。 良い予測ができるようになります緯度をバケット化することをおすすめします。 アイデア?
- 41.0 ~ 41.8
- 42.0 ~ 42.6
- 42.8 ~ 43.4
- 43.6 ~ 44.8
分位点バケット化
分位点バケット化は、バケット化の境界を作成し、 完全に同じか、ほぼ等しいと想定します。分位点バケット化 外れ値はほとんど非表示になります。
分位バケット化が解決する問題を説明するために、 等間隔のバケットを使用します。各バケットはそれぞれ、 10 個のバケットのうち、スパンは正確に 10,000 ドルに相当します。 0 ~ 10,000 のバケットに数十のサンプルが含まれていることに注意してください。 50,000 ~ 60,000 のバケットには 5 つの例しか含まれていません。 したがって、モデルには 0 ~ 10,000 のサンプルでトレーニングするのに十分なサンプルがあります。 十分な例がありません。

対照的に、次の図では、分位バケット化を使用して自動車価格を分割しています。 各バケットがほぼ同じ数のサンプルを持つビンに分割されます。 ビンには、範囲が狭いものもあれば、 非常に広範な価格帯が含まれています
