Trang này được dịch bởi Cloud Translation API.

Dữ liệu số: Chuẩn hoá

Sau khi kiểm tra dữ liệu thông qua các kỹ thuật thống kê và trực quan hoá, bạn nên chuyển đổi dữ liệu theo cách giúp mô hình huấn luyện hiệu quả hơn. Mục tiêu của việc bình thường hoá là biến đổi các đặc điểm để có cùng một quy mô. Ví dụ: hãy xem xét hai tính năng sau:

Tính năng X nằm trong khoảng từ 154 đến 24.917.482.
Tính năng Y nằm trong phạm vi từ 5 đến 22.

Hai tính năng này có phạm vi rất khác nhau. Quá trình chuẩn hoá có thể điều khiển X và Y để chúng nằm trong một phạm vi tương tự, có thể là từ 0 đến 1.

Việc chuẩn hoá mang lại các lợi ích sau:

Giúp các mô hình hội tụ nhanh hơn trong quá trình huấn luyện. Khi các đặc điểm khác nhau có các dải khác nhau, độ dốc giảm có thể "bật lại" và làm chậm quá trình hội tụ. Tuy nhiên, các trình tối ưu hoá nâng cao hơn như Adagrad và Adam sẽ ngăn chặn vấn đề này bằng cách thay đổi tốc độ học hiệu quả theo thời gian.
Giúp các mô hình dự đoán chính xác hơn. Khi các tính năng khác nhau có các phạm vi khác nhau, mô hình thu được có thể đưa ra dự đoán ít hữu ích hơn.
Giúp tránh "bẫy NaN" khi giá trị của đặc điểm rất cao. NaN là viết tắt của not a number (không phải số). Khi một giá trị trong mô hình vượt quá giới hạn độ chính xác dấu phẩy động, hệ thống sẽ đặt giá trị đó thành NaN thay vì một số. Khi một số trong mô hình trở thành NaN, các số khác trong mô hình cũng sẽ trở thành NaN.
Giúp mô hình tìm hiểu các trọng số phù hợp cho từng đặc điểm. Nếu không có tính năng điều chỉnh theo tỷ lệ, mô hình sẽ chú ý quá nhiều đến các tính năng có phạm vi rộng và không chú ý đủ đến các tính năng có phạm vi hẹp.

Bạn nên chuẩn hoá các đặc điểm dạng số có phạm vi khác nhau (ví dụ: tuổi và thu nhập). Bạn cũng nên chuẩn hoá một đặc điểm số duy nhất bao gồm nhiều phạm vi, chẳng hạn như city population.

Hãy xem xét hai tính năng sau:

Giá trị thấp nhất của tính năng A là -0,5 và giá trị cao nhất là +0,5.
Giá trị thấp nhất của tính năng B là -5.0 và giá trị cao nhất là +5.0.

Tính năng A và tính năng B có span tương đối hẹp. Tuy nhiên, span của Tính năng B rộng hơn 10 lần so với span của Tính năng A. Vì thế:

Khi bắt đầu huấn luyện, mô hình giả định rằng Tính năng B "quan trọng" gấp 10 lần so với Tính năng A.
Quá trình huấn luyện sẽ mất nhiều thời gian hơn dự kiến.
Mô hình thu được có thể không tối ưu.

Thiệt hại tổng thể do không chuẩn hoá sẽ tương đối nhỏ; tuy nhiên, bạn vẫn nên chuẩn hoá Tính năng A và Tính năng B theo cùng một tỷ lệ, có thể là từ -1,0 đến +1,0.

Bây giờ, hãy xem xét hai đặc điểm có độ chênh lệch lớn hơn về phạm vi:

Giá trị thấp nhất của tính năng C là -1 và giá trị cao nhất là +1.
Giá trị thấp nhất của tính năng D là +5000 và giá trị cao nhất là +1.000.000.000.

Nếu bạn không chuẩn hoá Tính năng C và Tính năng D, mô hình của bạn có thể sẽ không tối ưu. Hơn nữa, quá trình huấn luyện sẽ mất nhiều thời gian hơn để hội tụ hoặc thậm chí không thể hội tụ hoàn toàn!

Phần này trình bày 3 phương pháp chuẩn hoá phổ biến:

điều chỉnh theo tỷ lệ tuyến tính
Điều chỉnh theo điểm Z
chia tỷ lệ theo logarit

Phần này cũng đề cập đến việc cắt. Mặc dù không phải là kỹ thuật chuẩn hoá thực sự, nhưng việc cắt bớt sẽ giúp các đặc điểm số không theo quy tắc trở thành các dải tạo ra mô hình tốt hơn.

Chia độ tuyến tính

Điều chỉnh theo tỷ lệ tuyến tính (thường được rút gọn thành điều chỉnh theo tỷ lệ) có nghĩa là chuyển đổi các giá trị dấu phẩy động từ phạm vi tự nhiên thành phạm vi chuẩn – thường là từ 0 đến 1 hoặc từ -1 đến +1.

Nhấp vào biểu tượng để xem phép tính.

Sử dụng công thức sau để điều chỉnh theo phạm vi tiêu chuẩn từ 0 đến 1:

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

trong đó:

$x'$ là giá trị được điều chỉnh theo tỷ lệ.
$x$ là giá trị ban đầu.
$x_{min}$ là giá trị thấp nhất trong tập dữ liệu của đặc điểm này.
$x_{max}$ là giá trị cao nhất trong tập dữ liệu của đặc điểm này.

Ví dụ: hãy xem xét một đặc điểm có tên là quantity có phạm vi tự nhiên từ 100 đến 900. Giả sử giá trị tự nhiên của quantity trong một ví dụ cụ thể là 300. Do đó, bạn có thể tính giá trị chuẩn hoá là 300 như sau:

$x$ = 300
$x_{min}$ = 100
$x_{max}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

Bạn nên chọn phương pháp điều chỉnh theo tỷ lệ tuyến tính khi đáp ứng tất cả các điều kiện sau:

Giới hạn dưới và giới hạn trên của dữ liệu không thay đổi nhiều theo thời gian.
Biểu đồ chứa ít hoặc không có giá trị ngoại lai và các giá trị ngoại lai đó không quá lớn.
Tính năng này được phân phối gần như đồng đều trên phạm vi của nó. Tức là biểu đồ sẽ hiển thị các thanh gần như đồng đều cho hầu hết các giá trị.

Giả sử age của con người là một tính năng. Điều chỉnh tỷ lệ tuyến tính là một kỹ thuật chuẩn hoá tốt cho age vì:

Giới hạn dưới và giới hạn trên gần đúng là từ 0 đến 100.
age chứa một tỷ lệ phần trăm tương đối nhỏ các giá trị ngoại lai. Chỉ khoảng 0,3% dân số là trên 100 tuổi.
Mặc dù một số độ tuổi nhất định được thể hiện tốt hơn so với các độ tuổi khác, nhưng một tập dữ liệu lớn phải chứa đủ ví dụ về mọi độ tuổi.

Bài tập: Kiểm tra mức độ hiểu bài

Giả sử mô hình của bạn có một đặc điểm tên là net_worth chứa giá trị ròng của nhiều người. Việc điều chỉnh theo tỷ lệ tuyến tính có phải là kỹ thuật chuẩn hoá tốt cho net_worth không? Tại sao (hoặc tại sao lại không)?

Nhấp vào biểu tượng đó để xem câu trả lời.

Đáp án: Tỷ lệ tuyến tính sẽ là một lựa chọn không phù hợp để chuẩn hoá net_worth. Tính năng này chứa nhiều giá trị ngoại lai và các giá trị này không được phân phối đồng đều trên phạm vi chính. Hầu hết mọi người sẽ bị nén trong một dải rất hẹp của phạm vi tổng thể.

Điều chỉnh theo điểm Z

Điểm Z là số độ lệch chuẩn của một giá trị so với giá trị trung bình. Ví dụ: một giá trị lớn hơn 2 độ lệch chuẩn so với giá trị trung bình sẽ có điểm Z là +2.0. Một giá trị ít hơn 1,5 độ lệch chuẩn so với giá trị trung bình có điểm Z là -1,5.

Việc biểu thị một đặc điểm bằng tỷ lệ điểm Z có nghĩa là lưu trữ điểm Z của đặc điểm đó trong vectơ đặc điểm. Ví dụ: Hình sau đây cho thấy hai biểu đồ dạng thanh:

Ở bên trái, một phân phối chuẩn cổ điển.
Ở bên phải, cùng một phân phối được chuẩn hoá theo tỷ lệ điểm Z.

Hình 4. Hai biểu đồ: cả hai đều cho thấy phân phối chuẩn với
phân phối giống hệt nhau. Biểu đồ đầu tiên chứa dữ liệu thô có giá trị trung bình là 200 và độ lệch chuẩn là 30. Biểu đồ thứ hai chứa phiên bản điểm Z của phân phối thứ nhất có giá trị trung bình là 0 và độ lệch chuẩn là 1. — **Hình 4.** Dữ liệu thô (bên trái) so với điểm Z (bên phải) cho một phân phối chuẩn.

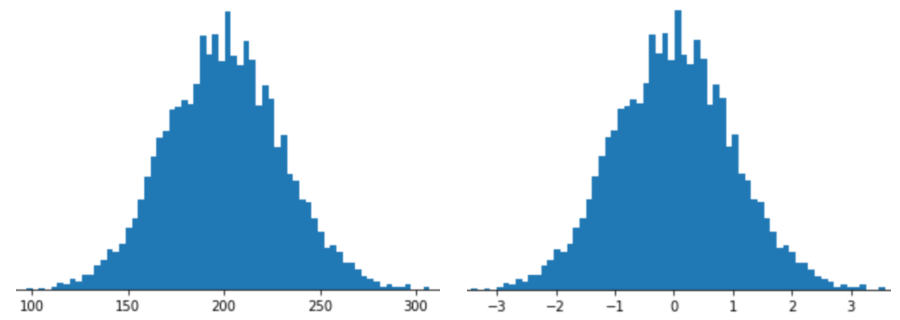
Việc điều chỉnh theo điểm Z cũng là một lựa chọn phù hợp cho dữ liệu như trong hình sau đây, dữ liệu này chỉ có phân phối chuẩn mơ hồ.

Hình 5. Hai biểu đồ có hình dạng giống hệt nhau, mỗi biểu đồ cho thấy một sự tăng mạnh lên một cao nguyên, sau đó giảm tương đối nhanh, theo sau là sự suy giảm dần. Một biểu đồ minh hoạ sự phân phối của dữ liệu thô; biểu đồ còn lại minh hoạ sự phân phối của dữ liệu thô khi được chuẩn hoá theo tỷ lệ điểm Z.
Các giá trị trên trục X của hai biểu đồ này rất khác nhau.
Biểu đồ dữ liệu thô trải dài từ 0 đến 29.000,trong khi biểu đồ theo tỷ lệ điểm Z dao động từ -1 đến khoảng +4, 8 — **Hình 5.** Dữ liệu thô (bên trái) so với tỷ lệ điểm Z (bên phải) cho một phân phối chuẩn không cổ điển.

Nhấp vào biểu tượng để xem phép tính.

Sử dụng công thức sau để chuẩn hoá một giá trị, $x$, thành điểm Z:

$$ x' = (x - μ) / σ $$

trong đó:

$x'$ là điểm Z.
$x$ là giá trị thô; tức là $x$ là giá trị bạn đang chuẩn hoá.
$μ$ là giá trị trung bình.
$σ$ là độ lệch chuẩn.

Ví dụ: giả sử:

mean = 100
độ lệch chuẩn = 20
giá trị ban đầu = 130

Vì thế:

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

Nhấp vào biểu tượng để tìm hiểu thêm về phân phối chuẩn.

Trong một phân phối chuẩn cổ điển:

Ít nhất 68,27% dữ liệu có điểm Z nằm trong khoảng từ -1 đến +1.
Ít nhất 95,45% dữ liệu có điểm Z nằm trong khoảng từ -2 đến +2.
Ít nhất 99,73% dữ liệu có điểm Z nằm trong khoảng từ -3 đến +3.
Ít nhất 99,994% dữ liệu có điểm Z nằm trong khoảng từ -4 đến +4.

Vì vậy, các điểm dữ liệu có điểm Z nhỏ hơn -4.0 hoặc lớn hơn +4.0 là rất hiếm, nhưng liệu chúng có thực sự là dữ liệu ngoại lai không? Vì điểm ngoại lai là một khái niệm không có định nghĩa nghiêm ngặt, nên không ai có thể nói chắc chắn. Xin lưu ý rằng một tập dữ liệu có đủ số lượng ví dụ sẽ gần như chắc chắn chứa ít nhất một vài ví dụ "hiếm" như vậy. Ví dụ: một đặc điểm có một tỷ ví dụ tuân theo một phân phối chuẩn cổ điển có thể có tới 60.000 ví dụ có điểm số nằm ngoài phạm vi -4, 0 đến +4,0.

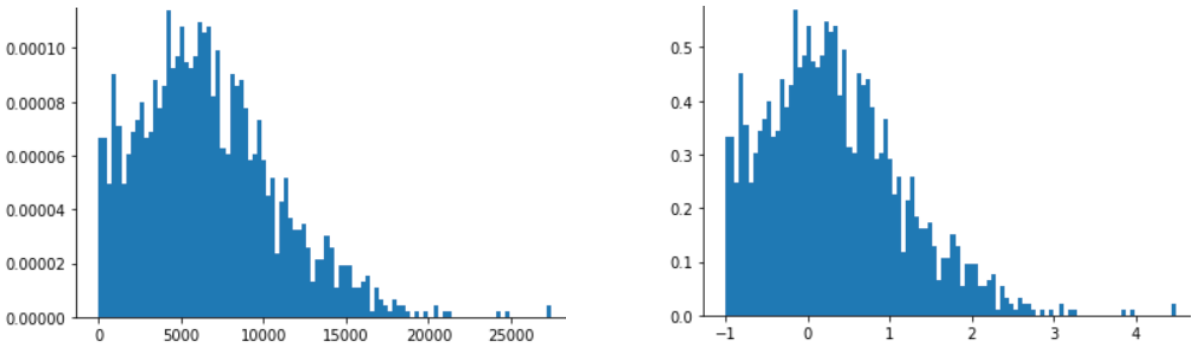
Điểm Z là một lựa chọn phù hợp khi dữ liệu tuân theo một phân phối chuẩn hoặc một phân phối tương tự như phân phối chuẩn.

Xin lưu ý rằng một số phân phối có thể là bình thường trong phần lớn phạm vi của chúng, nhưng vẫn chứa các giá trị ngoại lai cực đoan. Ví dụ: gần như tất cả các điểm trong một tính năng net_worth đều có thể vừa vặn với 3 độ lệch chuẩn, nhưng một vài ví dụ về tính năng này có thể cách trung bình hàng trăm độ lệch chuẩn. Trong những trường hợp này, bạn có thể kết hợp việc điều chỉnh theo điểm Z với một hình thức chuẩn hoá khác (thường là cắt bớt) để xử lý tình huống này.

Bài tập: Kiểm tra mức độ hiểu bài

Giả sử mô hình của bạn huấn luyện trên một đặc điểm có tên là height, chứa chiều cao của 10 triệu phụ nữ trưởng thành. Việc điều chỉnh theo điểm Z có phải là một kỹ thuật chuẩn hoá tốt cho height không? Tại sao (hoặc tại sao lại không)?

Nhấp vào biểu tượng đó để xem câu trả lời.

Đáp án: Điều chỉnh theo điểm Z sẽ là một kỹ thuật chuẩn hoá phù hợp cho height vì tính năng này tuân theo một phân phối chuẩn. 10 triệu ví dụ ngụ ý có rất nhiều giá trị ngoại lai – có thể đủ giá trị ngoại lai để mô hình học được các mẫu trên điểm Z rất cao hoặc rất thấp.

Chia tỷ lệ theo logarit

Tính năng điều chỉnh theo lôgarit sẽ tính lôgarit của giá trị thô. Về lý thuyết, lôgarit có thể là bất kỳ cơ số nào; trong thực tế, việc điều chỉnh theo lôgarit thường tính toán lôgarit tự nhiên (ln).

Nhấp vào biểu tượng để xem phép tính.

Sử dụng công thức sau để chuẩn hoá một giá trị, $x$, thành hàm logarit của giá trị đó:

$$ x' = ln(x) $$

trong đó:

$x'$ là logarit tự nhiên của $x$.
giá trị ban đầu = 54.598

Do đó, logarit của giá trị ban đầu là khoảng 4,0:

  4.0 = ln(54.598)

Việc điều chỉnh theo quy mô nhật ký sẽ hữu ích khi dữ liệu tuân theo một quy luật phân phối quy luật lũy thừa. Nói một cách đơn giản, hàm phân phối theo luật lũy thừa có dạng như sau:

Giá trị thấp của X có giá trị rất cao của Y.
Khi giá trị của X tăng lên, giá trị của Y sẽ nhanh chóng giảm xuống. Do đó, các giá trị cao của X có giá trị rất thấp của Y.

Điểm xếp hạng phim là một ví dụ điển hình về phân phối theo luật lũy thừa. Trong hình sau, hãy lưu ý:

Một số phim có nhiều điểm xếp hạng của người dùng. (Các giá trị thấp của X có giá trị cao của Y.)
Hầu hết các bộ phim đều có rất ít điểm xếp hạng của người dùng. (Các giá trị cao của X có giá trị thấp của Y.)

Việc điều chỉnh theo quy mô nhật ký sẽ thay đổi quá trình phân phối, giúp huấn luyện một mô hình sẽ đưa ra dự đoán chính xác hơn.

Hình 6. Hai biểu đồ so sánh dữ liệu thô với nhật ký dữ liệu thô.
Biểu đồ dữ liệu thô cho thấy nhiều điểm xếp hạng của người dùng ở đầu, theo sau là một đuôi dài. Biểu đồ nhật ký có mức phân phối đồng đều hơn. — **Hình 6.** So sánh một bản phân phối thô với nhật ký của bản phân phối đó.

Ví dụ thứ hai: doanh số bán sách tuân theo phân phối theo luật lũy thừa vì:

Hầu hết các cuốn sách được xuất bản đều bán được số lượng bản in rất nhỏ, có thể là một hoặc hai trăm bản.
Một số cuốn sách bán được số lượng bản in vừa phải, lên đến hàng nghìn bản.
Chỉ một số sách bán chạy nhất mới bán được hơn một triệu bản.

Giả sử bạn đang huấn luyện một mô hình tuyến tính để tìm mối quan hệ giữa, giả sử, ảnh bìa sách với doanh số bán sách. Một quy trình huấn luyện mô hình tuyến tính dựa trên các giá trị thô sẽ phải tìm thấy điều gì đó về ảnh bìa sách trên những cuốn sách bán được một triệu bản,tức là mạnh hơn 10.000 lần so với ảnh bìa sách chỉ bán được 100 bản. Tuy nhiên, việc điều chỉnh theo tỷ lệ logarit cho tất cả số liệu bán hàng sẽ giúp công việc này trở nên khả thi hơn nhiều. Ví dụ: logarit của 100 là:

  ~4.6 = ln(100)

trong khi logarit của 1.000.000 là:

  ~13.8 = ln(1,000,000)

Do đó, logarit của 1.000.000 chỉ lớn hơn logarit của 100 khoảng ba lần. Bạn có thể có thể tưởng tượng rằng ảnh bìa của một cuốn sách bán chạy có sức mạnh gấp ba lần (theo một cách nào đó) so với ảnh bìa của một cuốn sách bán rất ít.

Cắt

Cắt bớt là một kỹ thuật để giảm thiểu ảnh hưởng của các giá trị ngoại lai cực đoan. Tóm lại, việc cắt bớt thường giới hạn (giảm) giá trị của các giá trị ngoại lai xuống một giá trị tối đa cụ thể. Việc cắt bớt là một ý tưởng lạ, nhưng có thể rất hiệu quả.

Ví dụ: hãy tưởng tượng một tập dữ liệu chứa một đặc điểm có tên là roomsPerPerson, đại diện cho số phòng (tổng số phòng chia cho số người lưu trú) của nhiều ngôi nhà. Biểu đồ sau đây cho thấy hơn 99% giá trị đặc điểm tuân theo một phân phối chuẩn (gần như có giá trị trung bình là 1,8 và độ lệch chuẩn là 0,7). Tuy nhiên, tính năng này chứa một số giá trị ngoại lai, một số giá trị ngoại lai cực đoan:

Hình 7. Biểu đồ roomsPerPerson trong đó gần như tất cả các giá trị
đều nằm trong khoảng từ 0 đến 4, nhưng có một đuôi rất dài
kéo dài đến 17 phòng cho mỗi người — **Hình 7.** Chủ yếu là bình thường, nhưng không hoàn toàn bình thường.

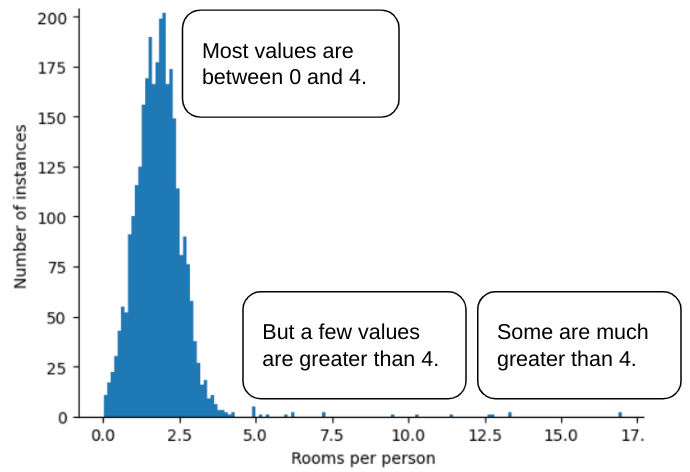
Làm cách nào để giảm thiểu ảnh hưởng của những giá trị ngoại lai cực đoan đó? Vâng, biểu đồ này không phải là một phân phối đều, phân phối chuẩn hoặc phân phối theo luật lũy thừa. Nếu bạn chỉ giới hạn hoặc cắt giá trị tối đa của roomsPerPerson ở một giá trị tuỳ ý, chẳng hạn như 4.0 thì sao?

Biểu đồ roomsPerPerson trong đó tất cả các giá trị nằm trong khoảng từ 0 đến
4.0. Biểu đồ có hình chuông, nhưng có một đỉnh bất thường ở 4,0 — **Hình 8.** Cắt bớt giá trị của đối tượng ở mức 4.0.

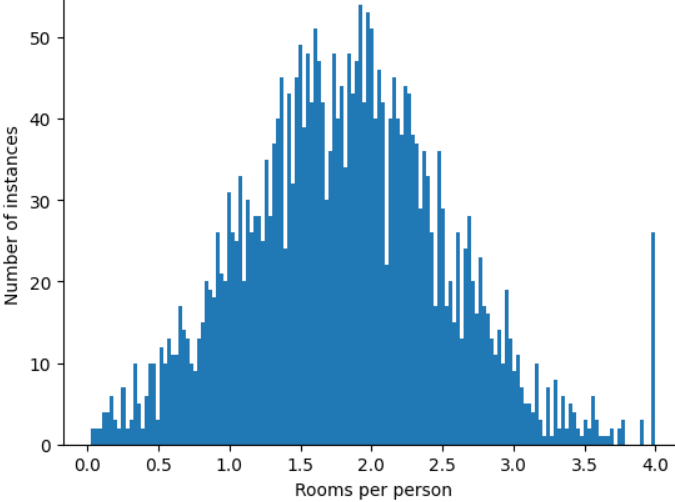
Việc cắt giá trị đặc điểm ở mức 4.0 không có nghĩa là mô hình của bạn bỏ qua tất cả giá trị lớn hơn 4.0. Thay vào đó, điều này có nghĩa là tất cả các giá trị lớn hơn 4.0 hiện trở thành 4.0. Điều này giải thích cho sự khác biệt ở 4.0. Mặc dù có đồi đó, nhưng tập hợp tính năng theo tỷ lệ hiện hữu ích hơn dữ liệu ban đầu.

Đợi một chút! Bạn có thực sự có thể giảm mọi giá trị ngoại lai xuống một ngưỡng trên tuỳ ý không? Có, khi huấn luyện mô hình.

Bạn cũng có thể cắt bớt các giá trị sau khi áp dụng các hình thức chuẩn hoá khác. Ví dụ: giả sử bạn sử dụng phương pháp điều chỉnh theo điểm Z, nhưng một vài giá trị ngoại lai có giá trị tuyệt đối lớn hơn nhiều so với 3. Trong trường hợp này, bạn có thể:

Cắt bớt các điểm số Z lớn hơn 3 để trở thành chính xác 3.
Cắt bớt các điểm số Z nhỏ hơn -3 để trở thành chính xác -3.

Tính năng cắt giúp mô hình của bạn không lập chỉ mục quá nhiều dữ liệu không quan trọng. Tuy nhiên, một số giá trị ngoại lai thực sự quan trọng, vì vậy, hãy cắt bớt các giá trị một cách cẩn thận.

Tóm tắt các kỹ thuật chuẩn hoá

Kỹ thuật chuẩn hoá	Công thức	Trường hợp sử dụng
Chia độ tuyến tính	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	Khi đặc điểm được phân phối đồng đều trên một phạm vi cố định.
Điều chỉnh theo điểm Z	$$ x' = \frac{x - μ}{σ}$$	Khi phân phối đặc điểm không chứa các giá trị ngoại lai cực đoan.
Chia tỷ lệ theo logarit	$$ x' = log(x)$$	Khi tính năng tuân theo quy luật hàm mũ.
Cắt	Nếu $x > max$, hãy đặt $x' = max$ Nếu $x < min$, hãy đặt $x' = min$	Khi đặc điểm chứa các giá trị ngoại lai cực đoan.

Bài tập: Kiểm tra kiến thức

Kỹ thuật nào phù hợp nhất để chuẩn hoá một đặc điểm có phân phối sau đây?

Biểu đồ thanh cho thấy một cụm dữ liệu có các giá trị trong khoảng từ 0 đến 200.000. Số điểm dữ liệu tăng dần trong phạm vi từ 0 đến 100.000, sau đó giảm dần từ 100.000 xuống 200.000.

Điều chỉnh theo điểm Z

Các điểm dữ liệu thường tuân theo một phân phối chuẩn, vì vậy, việc điều chỉnh theo điểm Z sẽ buộc các điểm dữ liệu đó nằm trong phạm vi –3 đến +3.

Chia độ tuyến tính

Xem lại nội dung thảo luận về các kỹ thuật chuẩn hoá trên trang này rồi thử lại.

Chia tỷ lệ theo logarit

Xem lại nội dung thảo luận về các kỹ thuật chuẩn hoá trên trang này rồi thử lại.

Cắt

Xem lại nội dung thảo luận về các kỹ thuật chuẩn hoá trên trang này rồi thử lại.

Giả sử bạn đang phát triển một mô hình dự đoán năng suất của trung tâm dữ liệu dựa trên nhiệt độ được đo lường bên trong trung tâm dữ liệu. Hầu hết các giá trị temperature trong tập dữ liệu của bạn nằm trong khoảng từ 15 đến 30 (C), ngoại trừ các trường hợp sau:

Một hoặc hai lần mỗi năm, vào những ngày cực nóng, một vài giá trị từ 31 đến 45 được ghi lại trong temperature.
Mỗi điểm thứ 1.000 trong temperature được đặt thành 1.000 thay vì nhiệt độ thực tế.

Kỹ thuật chuẩn hoá nào là hợp lý cho temperature?

Cắt bớt các giá trị ngoại lai trong khoảng từ 31 đến 45, nhưng xoá các giá trị ngoại lai có giá trị là 1.000

Giá trị 1.000 là lỗi và bạn nên xoá thay vì cắt.

Các giá trị từ 31 đến 45 là các điểm dữ liệu hợp lệ. Bạn nên cắt bớt các giá trị này, giả sử rằng tập dữ liệu không chứa đủ ví dụ trong phạm vi nhiệt độ này để huấn luyện mô hình nhằm đưa ra dự đoán chính xác. Tuy nhiên, trong quá trình suy luận, lưu ý rằng mô hình đã cắt sẽ đưa ra dự đoán giống nhau cho nhiệt độ 45 và nhiệt độ 35.

Cắt bỏ tất cả các giá trị ngoại lai

Xem lại nội dung thảo luận về các kỹ thuật chuẩn hoá trên trang này rồi thử lại.

Xoá tất cả các giá trị ngoại lai

Xem lại nội dung thảo luận về các kỹ thuật chuẩn hoá trên trang này rồi thử lại.

Xoá các giá trị ngoại lai từ 31 đến 45, nhưng cắt bớt các giá trị ngoại lai có giá trị là 1.000.

Xem lại nội dung thảo luận về các kỹ thuật chuẩn hoá trên trang này rồi thử lại.

Bài tập lập trình (10 phút)

Tiếp

Kết hợp (15 phút)