কখনও কখনও, যখন ML অনুশীলনকারীর ডোমেন জ্ঞান থাকে যে একটি ভেরিয়েবল অন্য একটি ভেরিয়েবলের বর্গক্ষেত্র, ঘনক্ষেত্র বা অন্যান্য শক্তির সাথে সম্পর্কিত, তখন বিদ্যমান সংখ্যাসূচক বৈশিষ্ট্যগুলির একটি থেকে একটি কৃত্রিম বৈশিষ্ট্য তৈরি করা কার্যকর।
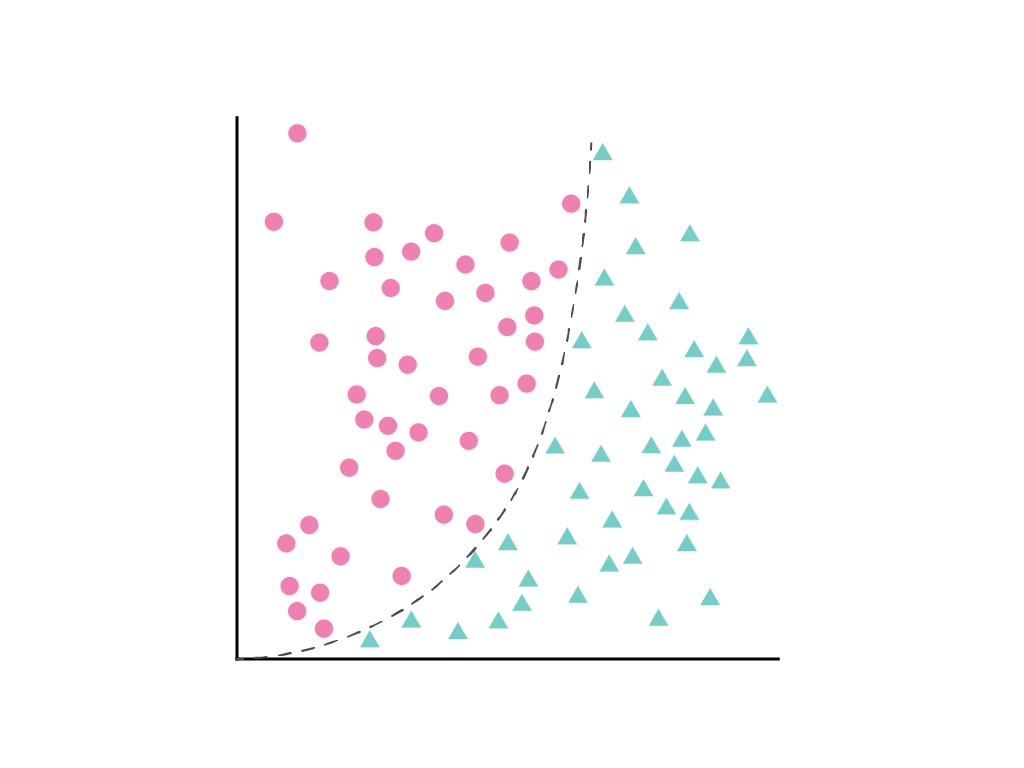
নিম্নলিখিত ডেটা পয়েন্টগুলির বিস্তার বিবেচনা করুন, যেখানে গোলাপী বৃত্তগুলি একটি শ্রেণী বা বিভাগ (উদাহরণস্বরূপ, গাছের একটি প্রজাতি) এবং সবুজ ত্রিভুজগুলি অন্য একটি শ্রেণি (বা গাছের প্রজাতি) প্রতিনিধিত্ব করে:
দুটি শ্রেণীকে পরিষ্কারভাবে আলাদা করে এমন একটি সরল রেখা আঁকা সম্ভব নয়, তবে এটি এমন একটি বক্ররেখা আঁকা সম্ভব :
লিনিয়ার রিগ্রেশন মডিউলে যেমন আলোচনা করা হয়েছে, একটি বৈশিষ্ট্য সহ একটি রৈখিক মডেল, $x_1$, রৈখিক সমীকরণ দ্বারা বর্ণনা করা হয়েছে:
অতিরিক্ত বৈশিষ্ট্য শর্তাবলী যোগ দ্বারা পরিচালিত হয় \(w_2x_2\),\(w_3x_3\), ইত্যাদি
গ্রেডিয়েন্ট ডিসেন্ট ওজন খুঁজে পায় $w_1$ (বা ওজন\(w_1\), \(w_2\), \(w_3\), অতিরিক্ত বৈশিষ্ট্যের ক্ষেত্রে) যা মডেলের ক্ষতি কমিয়ে দেয়। কিন্তু দেখানো তথ্য পয়েন্ট একটি লাইন দ্বারা পৃথক করা যাবে না. কি করা যায়?
রৈখিক সমীকরণ উভয়ই রাখা সম্ভব এবং একটি নতুন শব্দ সংজ্ঞায়িত করে অরৈখিকতার অনুমতি দেওয়া সম্ভব, \(x_2\), যে সহজভাবে \(x_1\) বর্গক্ষেত্র:
এই সিন্থেটিক বৈশিষ্ট্য, যাকে বহুপদী রূপান্তর বলা হয়, অন্য যে কোনো বৈশিষ্ট্যের মতোই বিবেচনা করা হয়। পূর্ববর্তী রৈখিক সূত্রটি হয়ে যায়:
এটি এখনও একটি রৈখিক রিগ্রেশন সমস্যা হিসাবে বিবেচনা করা যেতে পারে, এবং একটি লুকানো বর্গাকার শব্দ থাকা সত্ত্বেও, বহুপদী রূপান্তরটি স্বাভাবিকের মতো গ্রেডিয়েন্ট ডিসেন্টের মাধ্যমে নির্ধারিত ওজন। রৈখিক মডেল কীভাবে ট্রেন করে তা পরিবর্তন না করে, একটি বহুপদী রূপান্তর সংযোজন মডেলটিকে $y = b + w_1x + w_2x^2$ ফর্মের একটি বক্ররেখা ব্যবহার করে ডেটা পয়েন্টগুলিকে আলাদা করতে দেয়।
সাধারণত সুদের সংখ্যাগত বৈশিষ্ট্যটি নিজেই গুণিত হয়, অর্থাৎ কিছু শক্তিতে উত্থাপিত হয়। কখনও কখনও একজন এমএল অনুশীলনকারী উপযুক্ত সূচক সম্পর্কে একটি জ্ঞাত অনুমান করতে পারেন। উদাহরণস্বরূপ, ভৌত জগতের অনেক সম্পর্ক বর্গাকার পদের সাথে সম্পর্কিত, যার মধ্যে রয়েছে মহাকর্ষের কারণে ত্বরণ, দূরত্বের উপর আলো বা শব্দের ক্ষয় এবং স্থিতিস্থাপক সম্ভাব্য শক্তি।
শ্রেণীবদ্ধ ডেটাতে একটি সম্পর্কিত ধারণা হল বৈশিষ্ট্য ক্রস , যা প্রায়শই দুটি ভিন্ন বৈশিষ্ট্যকে সংশ্লেষ করে।