في بعض الأحيان، عندما يكون لدى ممارس الذكاء الاصطناعي معرفة بالموضوع تشير إلى أنّ متغيّرًا واحدًا مرتبط بمربع متغيّر آخر أو مكعبه أو أيّ درجة أخرى من السمات الحالية، يكون من المفيد إنشاء سمة اصطناعية من أحد السمات الرقمية الحالية.
فكِّر في الانتشار التالي لنقاط البيانات، حيث تمثّل الدوائر الوردية فئة أو تصنيفًا واحدًا (مثلاً، نوع من الأشجار) والمثلثات الخضراء فئة أخرى (أو نوعًا آخر من الأشجار):
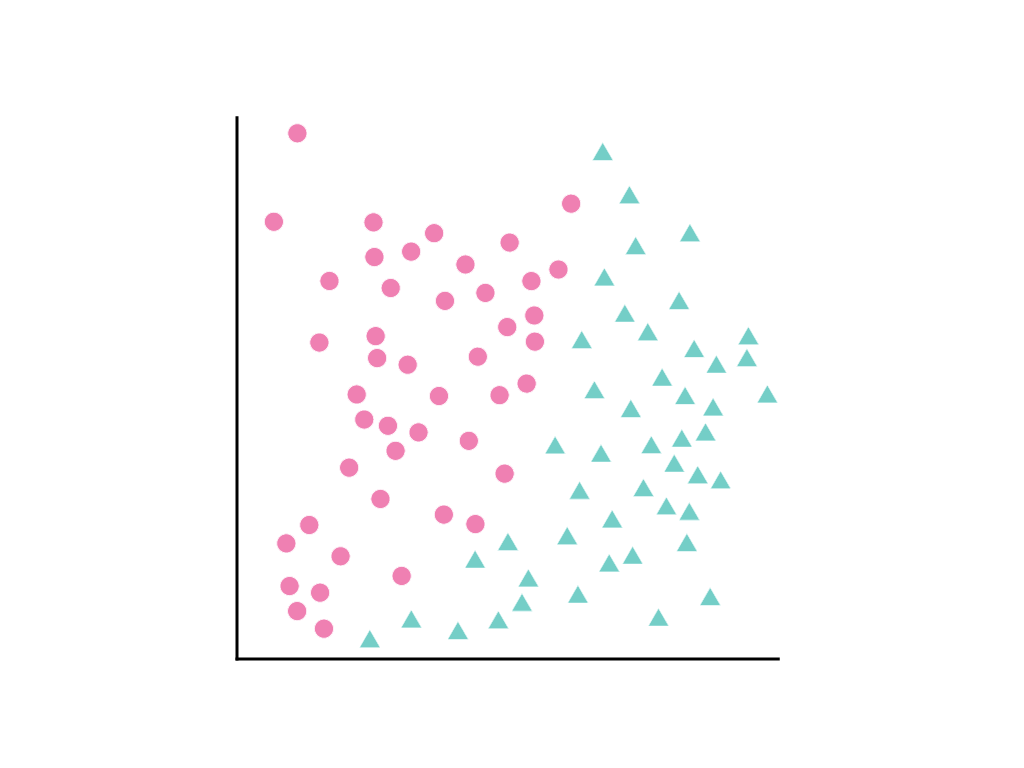
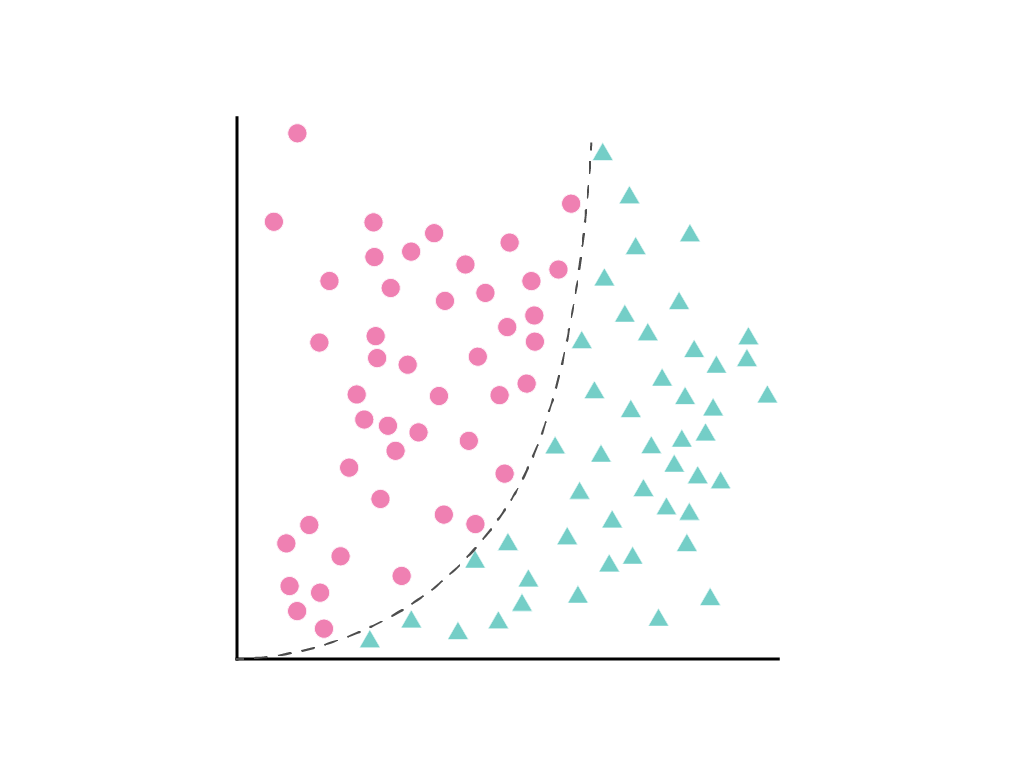
لا يمكن رسم خط مستقيم يفصل بين الفئتَين بوضوح، ولكن يمكن رسم منحنى يفصل بينهما:
كما هو موضّح في وحدة الانحدار الخطي، يتم وصف نموذج خطي يتضمّن سمة واحدة، وهي $x_1$، بالمعادلة الخطية التالية:
يتم التعامل مع الميزات الإضافية من خلال إضافة المصطلحات \(w_2x_2\) \(w_3x_3\)وما إلى ذلك.
تبحث الطريقة التنازلية للانحدار عن المرجح $w_1$ (أو المرجحين \(w_1\)و \(w_2\)و \(w_3\)في حال توفّر ميزات إضافية) الذي يقلل إلى أدنى حدّ من خسارة النموذج. ولكن لا يمكن فصل نقاط البيانات المعروضة بخط. ما الذي يمكنني فعله؟
من الممكن الاحتفاظ بالمعادلة الخطية والسماح بعدم الخطية من خلال تحديد مصطلح جديد، \(x_2\)، وهو ببساطة \(x_1\) مربّع:
تُعامل هذه الميزة الاصطناعية، التي تُعرف باسم التحويل المتعدد الحدود، مثل أي ميزة أخرى. تصبح الصيغة الخطية السابقة على النحو التالي:
لا يزال بالإمكان التعامل مع ذلك على أنّه مشكلة الانحدار الخطي ، ويتم تحديد الأوزان من خلال التدرج التنازلي كالمعتاد، على الرغم من احتوائها على مصطلح مربّع مخفي، وهو التحويل المتعدّد الحدود. بدون تغيير طريقة تدريب النموذج الخطي، تسمح إضافة تحويل متعدد الحدود لل النموذج بفصل نقاط البيانات باستخدام منحنى من الشكل $y = b + w_1x + w_2x^2$.
عادةً ما يتم ضرب السمة الرقمية المعنيّة بنفسها، أي يتم رفعها إلى بعض الأسس. في بعض الأحيان، يمكن لأحد خبراء الذكاء الاصطناعي إجراء تخمين مدروس حول الأس المناسب. على سبيل المثال، ترتبط العديد من العلاقات في الصعيد الفيزيائي بعوامل مربّعة، بما في ذلك التسارع الناتج عن الجاذبية، وتلاشي الضوء أو الصوت على مسافة معيّنة، والطاقة الكامنة المرنة.
إذا كنت تحوّل سمة بطريقة تغيّر مقياسها، ننصحك بالتفكير في تجربة تسويتها أيضًا. قد يؤدي تسويف البيانات بعد تحويلها إلى تحسين أداء النموذج. لمزيد من المعلومات، يُرجى الاطّلاع على البيانات الرقمية: التسويّة.
من المفاهيم ذات الصلة في البيانات الفئوية هو تداخل الميزة، الذي يجمع بين سمتَين مختلفتَين بشكلٍ متكرّر.