Czasami, gdy specjalista od uczenia maszynowego ma wiedzę z danej dziedziny, która sugeruje, że jedna zmienna jest powiązana z kwadratem, sześcianem lub inną potęgą innej zmiennej, warto utworzyć cechę syntetyczną na podstawie jednej z dostępnych cech liczbowych.
Rozważ rozrzut punktów danych, gdzie różowe kółka reprezentują jedną klasę lub kategorię (np. gatunek drzewa), a zielone trójkąty inną klasę (lub gatunek drzewa):
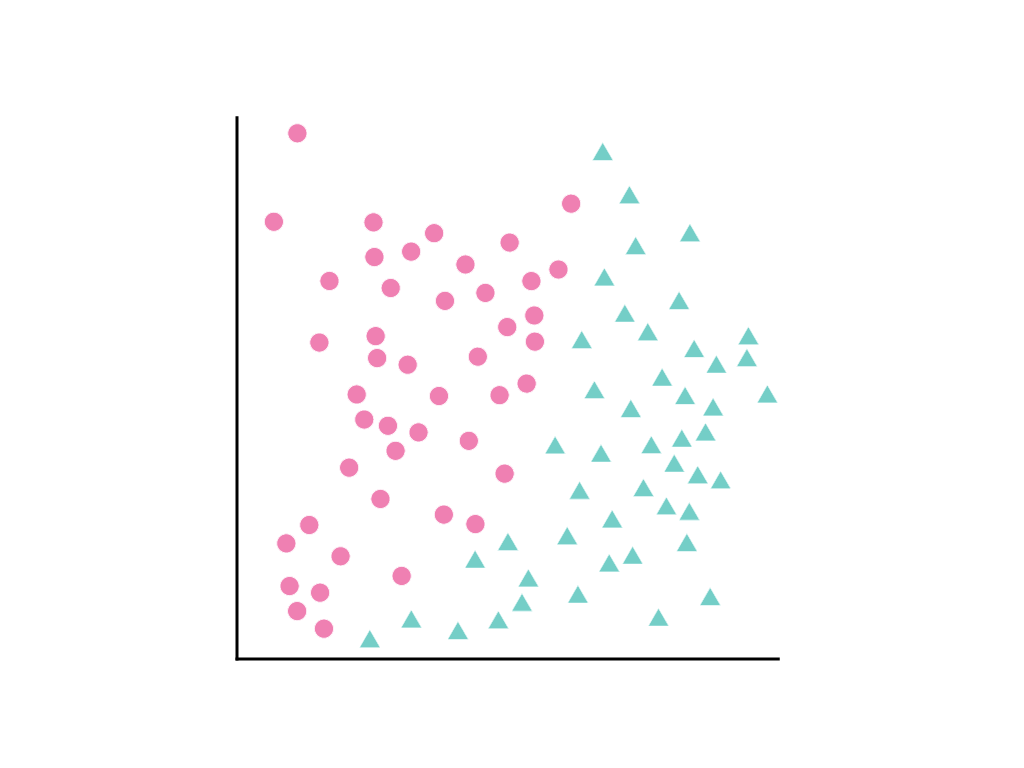
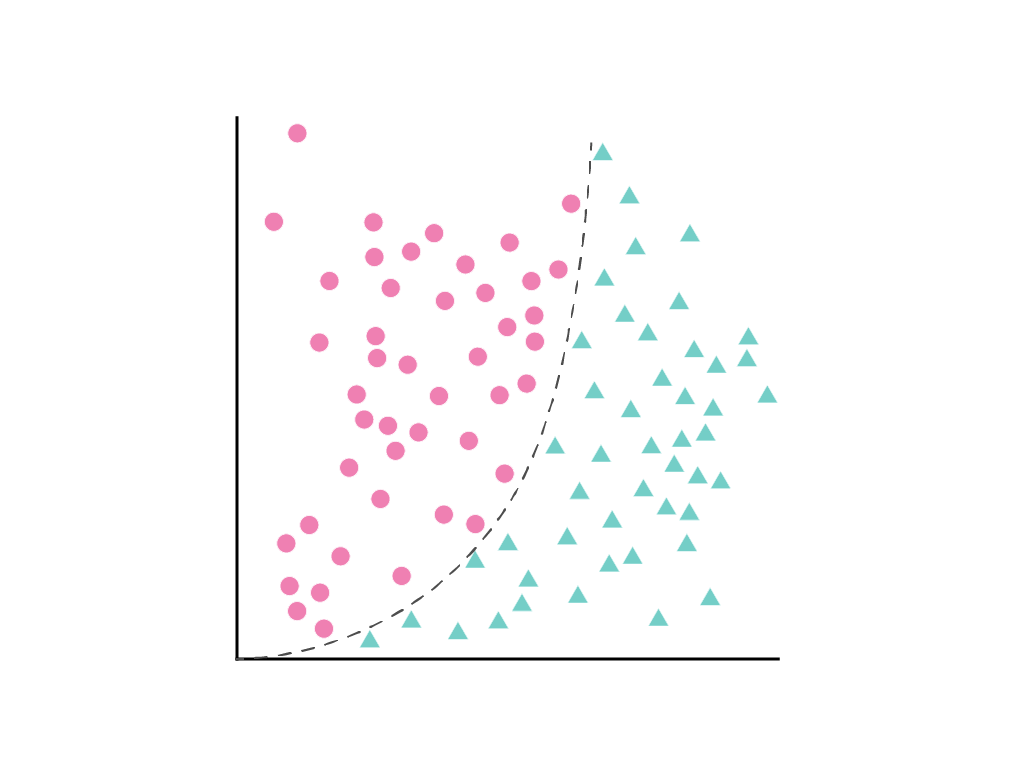
Nie można narysować linii prostej, która wyraźnie oddziela obie klasy, ale można narysować krzywą:
Jak opisano w module Regresja liniowa, model liniowy z 1 cechą, $x_1$, jest opisany równaniem liniowym:
Dodatkowe funkcje są obsługiwane przez dodawanie warunków \(w_2x_2\), \(w_3x_3\)itp.
Metoda gradientu prostego znajduje wagę $w_1$ (lub wagi\(w_1\), \(w_2\), \(w_3\)w przypadku dodatkowych funkcji), która minimalizuje stratę modelu. Punkty danych nie mogą być jednak rozdzielone linią. Co można zrobić w tej sprawie?
Można zachować równanie liniowe i zezwolić na nieliniowości,definiując nowy termin \(x_2\), który jest po prostu kwadratem \(x_1\) :
Ta syntetyczna cecha, zwana transformatem wielomianowym, jest traktowana jak każda inna cecha. Poprzednia formuła liniowa staje się:
Można je nadal traktować jak problem regresji liniowej, a wagi określane jak zwykle za pomocą zejścia gradientu, mimo że zawiera ona ukryty człon kwadratowy, czyli transformację wielomianową. Dodanie transformacji wielomianowej pozwala modelowi oddzielić punkty danych za pomocą krzywej w postaci $y = b + w_1x + w_2x^2$, nie zmieniając sposobu trenowania modelu liniowego.
Zwykle interesująca cecha liczbowa jest mnożona przez siebie, czyli podnoszona do jakiejś potęgi. Czasami specjalista od uczenia maszynowego może zgadnąć odpowiedni wykładnik. Na przykład wiele zależności w świecie fizycznym jest związanych z wykładnikami kwadratowymi, w tym przyspieszeniem ziemskim, tłumieniem światła lub dźwięku na odległość oraz sprężystym potencjałem energii.
Jeśli przekształcisz cechę w sposób, który zmienia jej skalę, rozważ jej znormalizowanie. Normalizacja po przekształceniu może poprawić skuteczność modelu. Więcej informacji znajdziesz w artykule Dane liczbowe: normalizacja.
Powiązaną koncepcją w przypadku danych kategorialnych jest krzyżowanie cech, które częściej łączy 2 różne cechy.