勾配降下法は、損失が最小になるモデルを生成する重みとバイアスを反復的に見つける数学的手法です。勾配降下法では、ユーザー定義の反復回数だけ次のプロセスを繰り返して、最適な重みとバイアスを見つけます。
モデルは、ゼロに近いランダムな重みとバイアスでトレーニングを開始し、次の手順を繰り返します。
現在の重みとバイアスで損失を計算します。
損失を減らす重みとバイアスを移動する方向を決定します。
損失を減らす方向に重みとバイアスの値を少しずつ移動します。
ステップ 1 に戻り、モデルが損失をさらに減らすことができなくなるまで、このプロセスを繰り返します。
次の図は、勾配降下法が損失が最小のモデルを生成する重みとバイアスを見つけるために実行する反復ステップの概要を示しています。
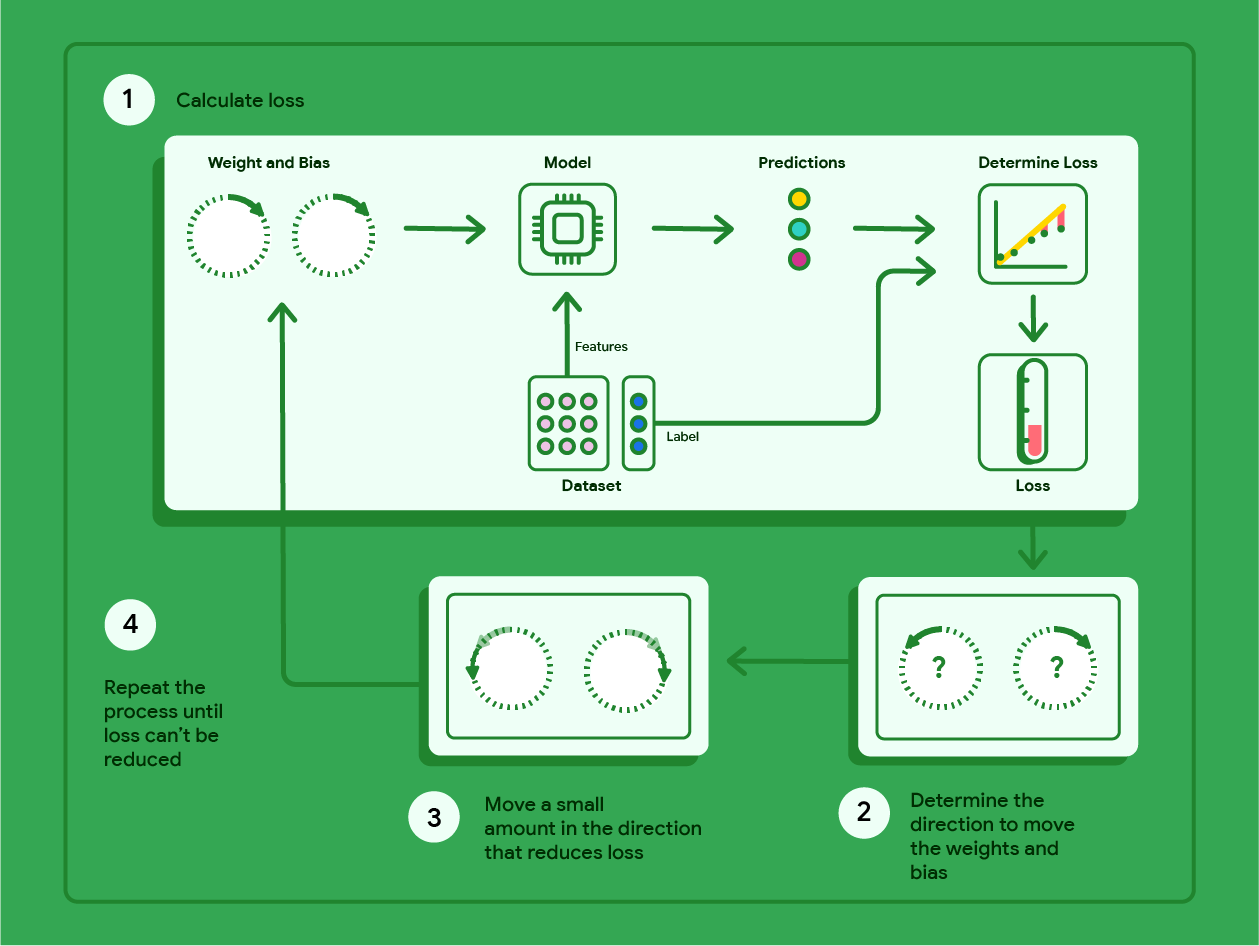
図 11. 勾配降下法は、損失が最小になるモデルを生成する重みとバイアスを見つける反復プロセスです。
プラスアイコンをクリックすると、勾配降下法の背後にある数学について詳しく確認できます。
具体的なレベルでは、車の重量(ポンド)と燃費(マイル / ガロン)の 7 つの例を含む小さなデータセットを使用して、勾配降下法のステップを確認できます。
| ポンド(1,000 単位)(特徴) | マイル / ガロン(ラベル) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- モデルは、重みとバイアスをゼロに設定してトレーニングを開始します。
- 現在のモデル パラメータで MSE 損失を計算します。
- 各重みとバイアスにおける損失関数の接線の傾きを計算します。
- 負の傾斜の方向に少し移動して、次の重みとバイアスを取得します。ここでは、便宜的に「少額」を 0.01 と定義します。
プラスアイコンをクリックすると、傾斜の計算方法が表示されます。
重みとバイアスに接する線の傾きを取得するには、重みとバイアスに関する損失関数の導関数を取得し、方程式を解きます。
予測を行う方程式は $ f_{w,b}(x) = (w*x)+b $ と記述します。
実際の値は $ y $ とします。
MSE は次の式で計算します。
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
ここで、$i$ は $ith$ トレーニング例、$M$ は例の数を表します。
重みに関する損失関数の導関数は次のように記述されます。
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
次の値に評価されます。
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
まず、予測値から実際の値を減算した値を合計し、その値を特徴値の 2 倍で乗算します。次に、合計を例の数で割ります。結果は、重みの値に接する線の傾きです。
重みとバイアスを 0 にしてこの方程式を解くと、直線の傾きは -119.7 になります。
バイアスの導関数
バイアスに関する損失関数の導関数は次のように記述されます。
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
次のように評価されます。
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
まず、各予測値から実測値を減算した値を合計し、その結果に 2 を掛けます。次に、合計を例の数で割ります。結果は、バイアスの値に接する線の傾きです。
重みとバイアスを 0 にしてこの方程式を解くと、線の傾きは -34.3 になります。
新しい重みとバイアスを使用して損失を計算し、これを繰り返します。このプロセスを 6 回繰り返すと、次の重み、バイアス、損失が得られます。
| 繰り返し | 重量 | バイアス | 損失(MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
重みとバイアスが更新されるたびに損失が減少していることがわかります。この例では、6 回の反復処理後に停止しました。実際には、モデルは収束するまでトレーニングされます。モデルが収束すると、勾配降下法によって損失をほぼ最小限に抑える重みとバイアスが見つかるため、追加のイテレーションを行っても損失は減少しません。
モデルが収束を超えてトレーニングを続けると、モデルがパラメータを最小値付近で継続的に更新するため、損失がわずかに変動し始めます。これにより、モデルが実際に収束したことを確認することが難しくなる可能性があります。モデルが収束したことを確認するには、損失が安定するまでトレーニングを続けます。
モデルの収束と損失曲線
モデルをトレーニングするときは、損失曲線を見て、モデルが収束したかどうかを判断することがよくあります。損失曲線は、モデルのトレーニング中に損失がどのように変化するかを示します。一般的な損失曲線は次のようになります。Y 軸が損失、X 軸がイテレーションです。
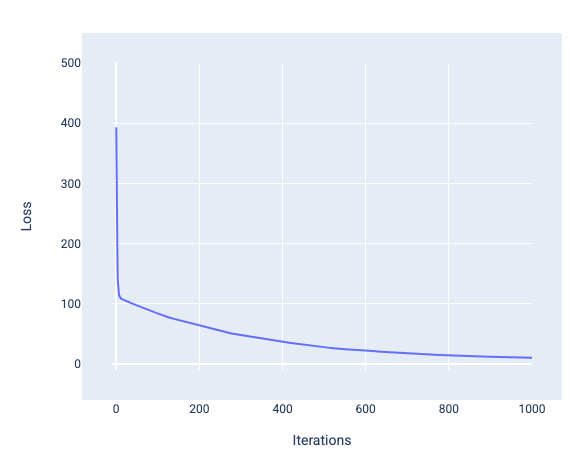
図 12. モデルが 1,000 回目の反復処理のマーク付近で収束していることを示す損失曲線。
最初の数回の反復処理で損失が大幅に減少し、その後徐々に減少して、1,000 回目の反復処理あたりで平坦になっていることがわかります。1,000 回のイテレーション後、モデルが収束したとほぼ確信できます。
次の図では、トレーニング プロセスの開始時、中間時、終了時の 3 つのポイントでモデルを描画しています。トレーニング プロセスのスナップショットでモデルの状態を可視化すると、重みとバイアスの更新、損失の削減、モデルの収束の関連性が明確になります。
図では、特定のイテレーションで導出された重みとバイアスを使用してモデルを表します。データポイントとモデル スナップショットのグラフでは、モデルからデータポイントまでの青い損失線が損失の量を示しています。線が長いほど、損失が大きくなります。
次の図では、2 回目のイテレーション付近で損失が大きいため、モデルの予測精度が低下していることがわかります。
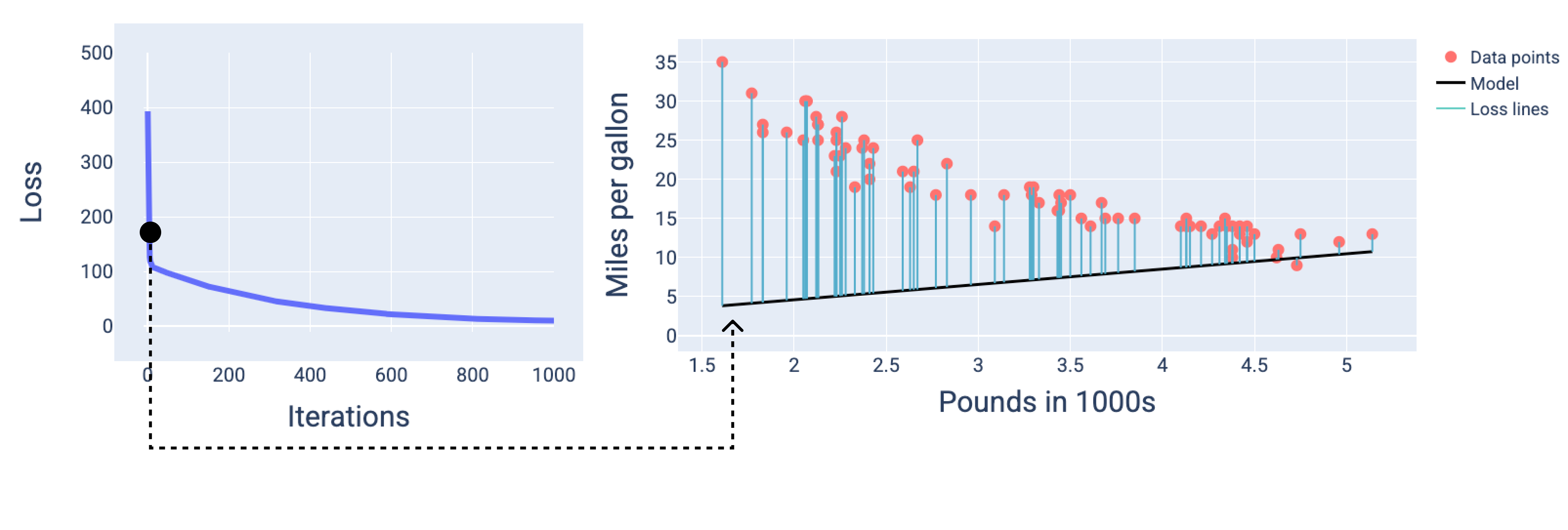
図 13. トレーニング プロセスの開始時の損失曲線とモデルのスナップショット。
400 回目の反復あたりで、勾配降下法によって、より優れたモデルを生成する重みとバイアスが見つかったことがわかります。
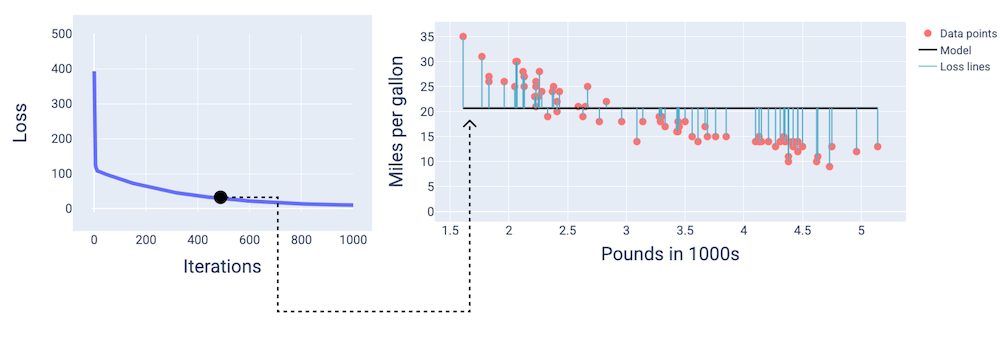
図 14. トレーニングの中間付近の損失曲線とモデルのスナップショット。
約 1,000 回の反復で、モデルが収束し、損失が最小限に抑えられたモデルが生成されていることがわかります。
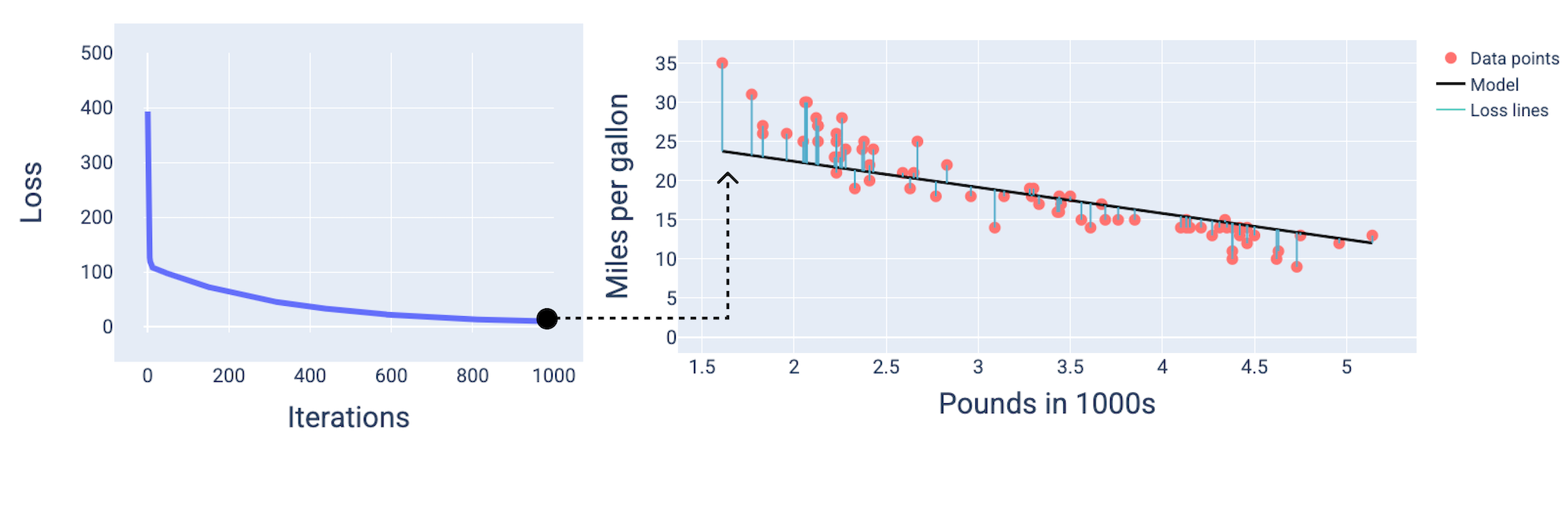
図 15. 損失曲線とトレーニング プロセスの終了近くのモデルのスナップショット。
演習: 理解度を確認する
収束と凸関数
線形モデルの損失関数は、常に凸面を生成します。このプロパティの結果として、線形回帰モデルが収束すると、モデルが最小の損失を生成する重みとバイアスを見つけたことがわかります。
1 つの特徴を持つモデルの損失曲面をグラフにすると、その凸形状を確認できます。次の図は、仮想の燃費データセットの損失曲面です。重みは x 軸、バイアスは y 軸、損失は z 軸に表示されます。
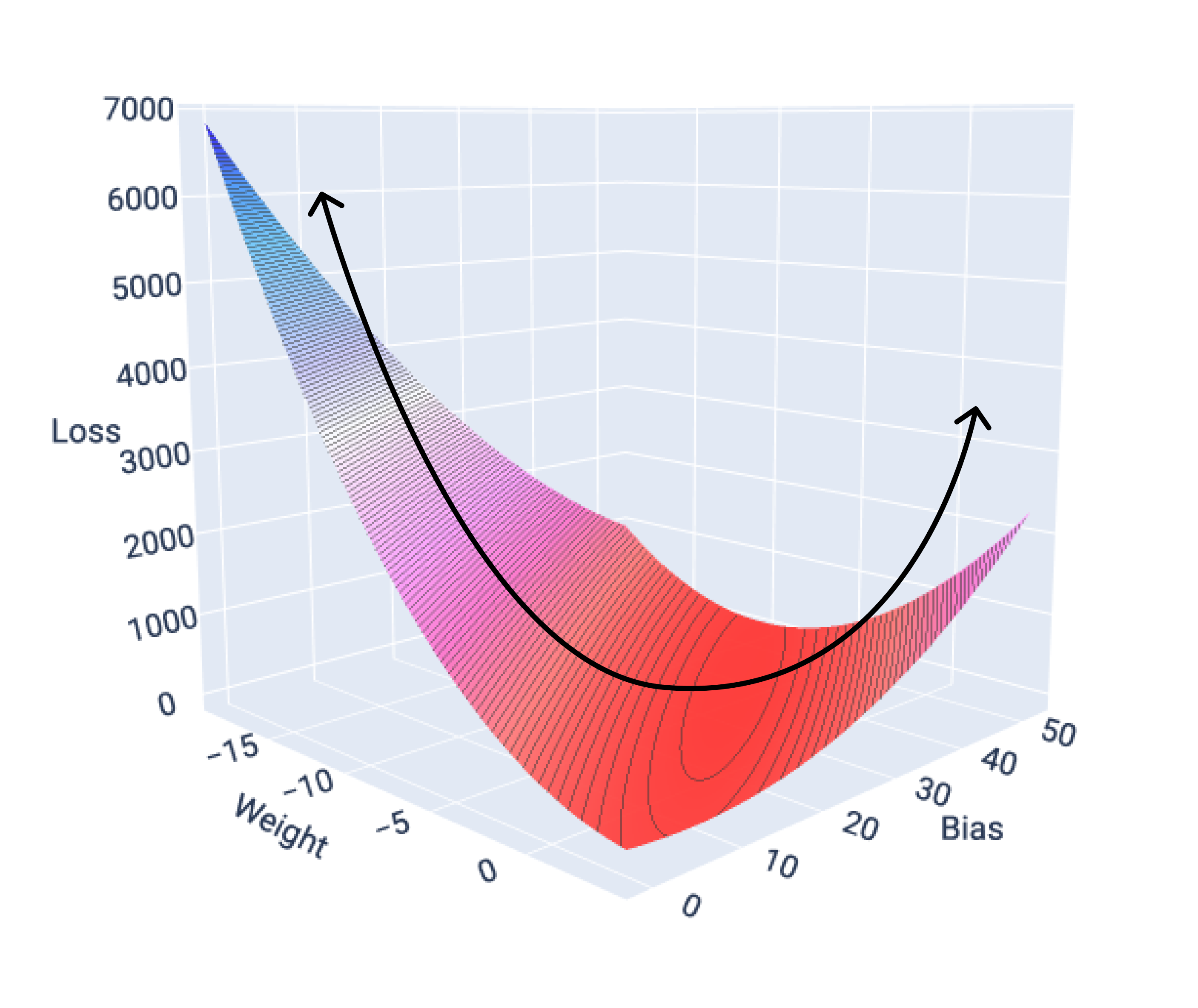
図 16. 凸形状を示す損失曲面。
この例では、重み -5.44 とバイアス 35.94 で損失が最小の 5.54 になります。
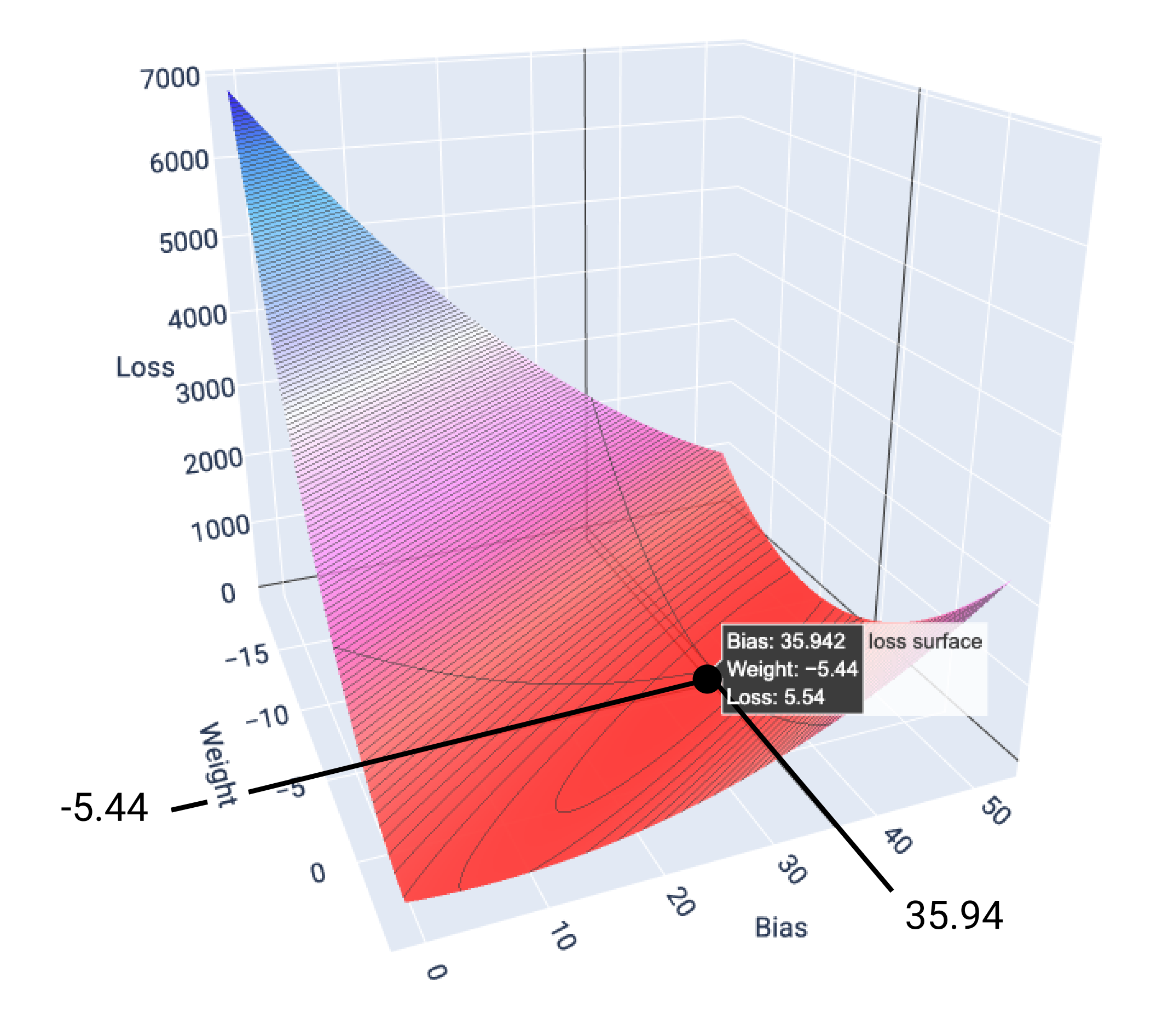
図 17. 損失が最小になる重みとバイアスの値を示す損失曲面。
線形モデルは、最小損失が見つかると収束します。したがって、追加の反復では、勾配降下法によって重みとバイアスの値が最小値の周辺でわずかに移動するだけです。勾配降下法で重みとバイアス点をグラフにすると、点は丘を転がり落ちるボールのように見え、最終的に下り坂がなくなった点で止まります。
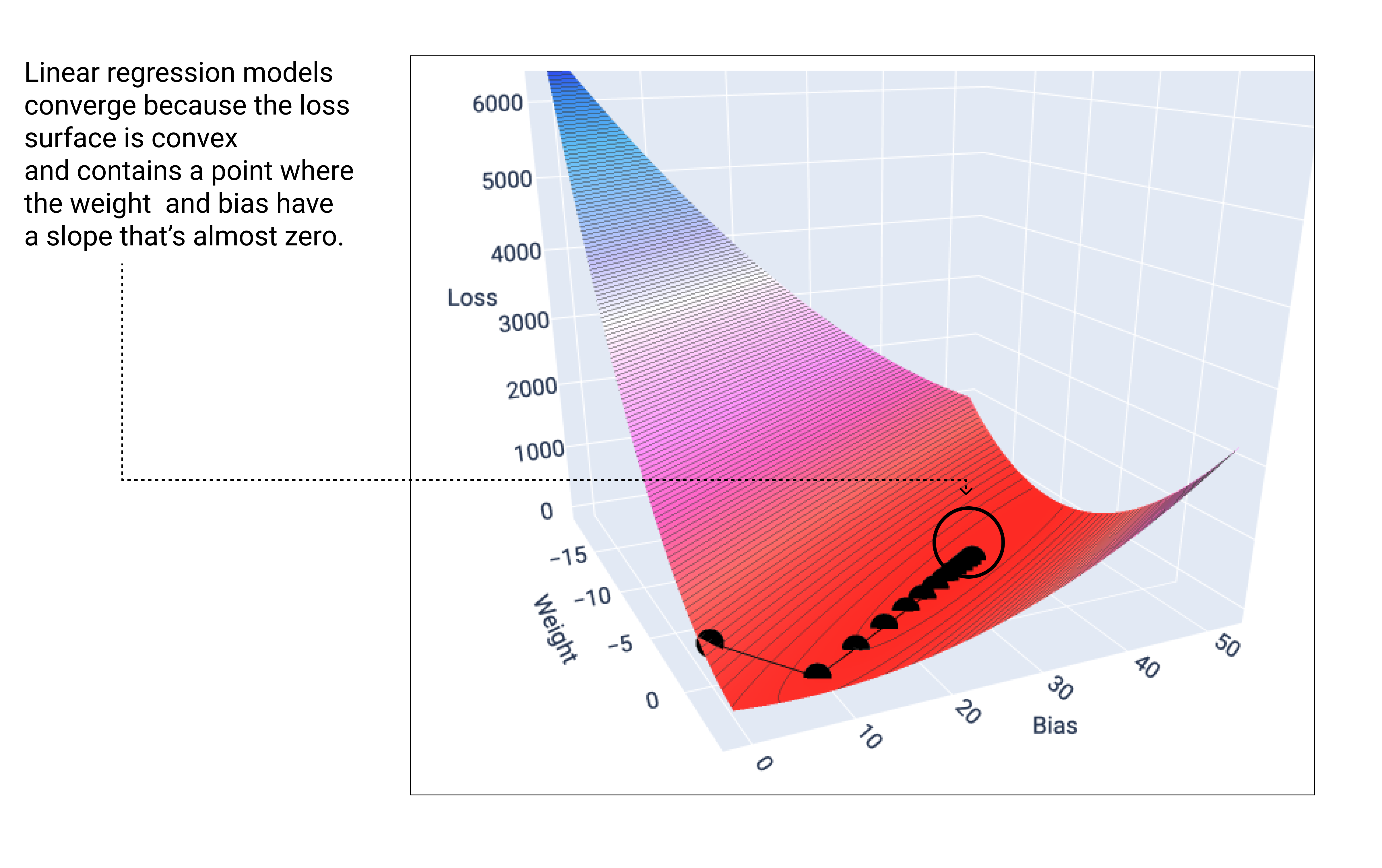
図 18. 損失グラフ。グラフの最低点で停止する勾配降下点を示しています。
黒い損失点が損失曲線の形状を正確に表していることに注目してください。損失曲線の形状は、急激に減少してから、損失曲面の最低点に達するまで徐々に減少する形状です。
モデルが各重みとバイアスの正確な最小値を検出することはほとんどなく、それに非常に近い値を検出することに注意してください。重みとバイアスの最小値は損失がゼロになる値ではなく、そのパラメータで最小の損失を生成する値であることに注意することも重要です。
損失が最小になる重みとバイアスの値(この場合は重みが -5.44、バイアスが 35.94)を使用して、モデルをグラフ化し、データへの適合度を確認します。
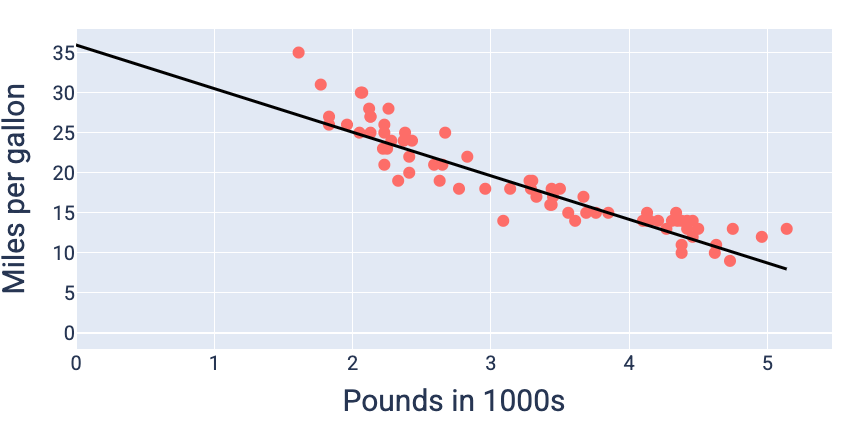
図 19. 損失が最小になる重みとバイアスの値を使用してグラフ化したモデル。
このデータセットでは、これ以外の重みとバイアスの値で損失がより少ないモデルを生成できないため、これが最適なモデルになります。
