Dans la section précédente, nous avons évalué l'équité de notre modèle d'admission à l'aide de parité démographique, en comparant les taux d'acceptation globaux pour les deux groupes démographiques.
Nous pourrions également comparer les taux d'acceptation pour les seuls taux d'acceptation des candidats du groupe majoritaire et du groupe minoritaire. Si les taux d'acceptation que tous les élèves qualifiés des deux groupes soient égaux, le modèle présente Égalité des chances: les étudiants ayant notre libellé préféré ("qualifiés pour l'admission") ont un total de de chances d'être acceptés, quel que soit le groupe démographique auquel ils appartiennent. auxquelles vous souhaitez vous connecter.
Reprenons le pool de candidats de la section précédente:
| Groupe majoritaire | Groupe minoritaire | |
|---|---|---|
| Qualifié | 35 | 15 |
| Non qualifié | 45 | 5 |
Supposons que le modèle d'admissions accepte 14 candidats du groupe majoritaire et six candidats du groupe minoritaire. Les décisions du modèle satisfont l'égalité des chances, comme le taux d'acceptation à la fois pour la majorité qualifiée et les candidats issus de minorités qualifiées est de 40%.
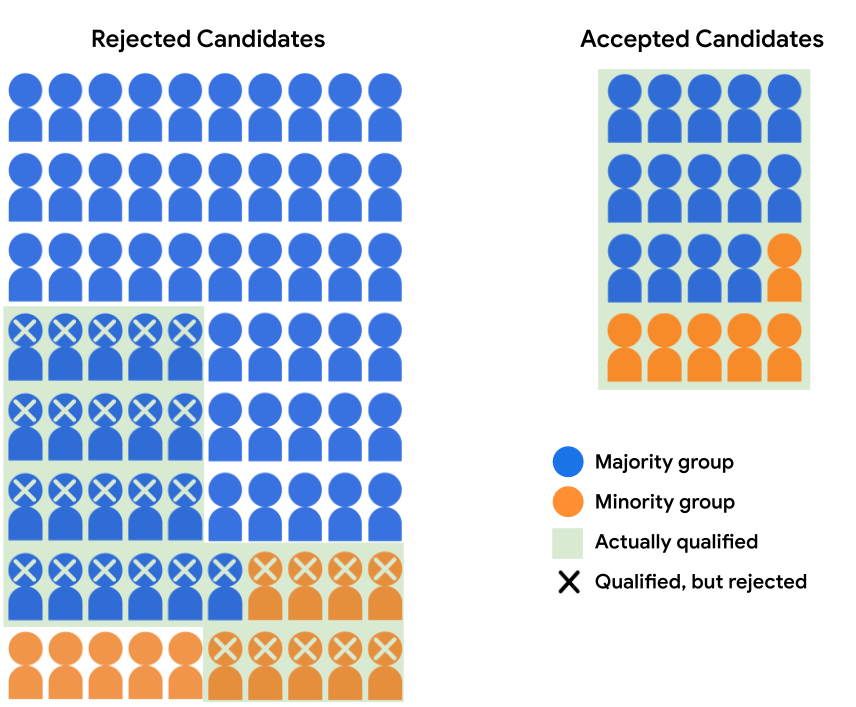
Le tableau suivant quantifie les nombres accompagnant les demandes candidats comme indiqué dans la Figure 4.
| Groupe majoritaire | Groupe minoritaire | |||
|---|---|---|---|---|
| Accepté | Refusé | Accepté | Refusé | |
| Qualifié | 14 | 21 | 6 | 9 |
| Non qualifié | 0 | 45 | 0 | 5 |
Avantages et inconvénients
Le principal avantage de l'égalité des chances est qu'elle permet le rapport entre les prédictions positives et négatives varie selon les groupes démographiques. à condition que le modèle puisse prédire l'étiquette préférée de la même manière ("qualifié(e) pour l'admission") aux deux groupes.
Les prédictions du modèle de la figure 4 ne satisfont pas à la parité démographique. en tant qu'étudiant dans le groupe majoritaire, a 17,5% de chances d'être accepté. un étudiant du groupe minoritaire a 30% de chances d'être accepté. Toutefois, un étudiant qualifié a 40% de chances d'être accepté, quel que soit du groupe auquel ils appartiennent, ce qui est sans doute plus juste dans ce cas. un cas d'utilisation particulier du modèle.
L'un des inconvénients de l'égalité des chances est qu'elle est conçue pour être utilisée les cas où il existe un libellé préféré clairement défini. S'il est tout aussi important que le modèle prédise à la fois la classe positive ("qualifié(e) pour l'admission") et la classe négative ("non éligible pour l'admission") pour tous les groupes démographiques. il peut être judicieux d'utiliser plutôt la métrique cotes égales, qui applique des taux de réussite égaux pour les deux étiquettes.
Un autre inconvénient de l'égalité
des chances est qu'elle évalue l'impartialité
en comparant les taux d'erreur agrégés des groupes démographiques, ce qui peut
ne sera pas toujours réalisable. Par exemple, si l'ensemble de données de notre modèle d'admissions
n'avait pas la caractéristique demographic_group, il ne serait pas possible de
répartir les taux d'acceptation des candidats à la majorité qualifiée et des candidats issus de minorités
et les comparer pour voir si l’égalité des chances est satisfaite.
Dans la section suivante, nous examinerons une autre métrique d'équité : l’impartialité, qui peut être utilisée dans des scénarios où les données démographiques ne existent pour tous les exemples.
Exercice: tester vos connaissances
Les prédictions d'un modèle peuvent répondre à la fois aux critères démographiques la parité et l'égalité des chances.
Prenons l'exemple d'un classificateur binaire (dont l'étiquette préférée est la classe positive) est évaluée sur 100 exemples, avec des résultats indiquées dans les matrices de confusion suivantes, décomposées par groupe démographique (majorité et minorité):
| Groupe majoritaire | Groupe minoritaire | |||
|---|---|---|---|---|
| Valeur positive prédite | Valeur négative prédite | Valeur positive prédite | Valeur négative prédite | |
| Valeur réelle positive | 6 | 12 | 3 | 6 |
| Valeur réelle négative | 10 | 36 | 6 | 21 |
|
\(\text{Positive Rate} = \frac{6+10}{6+10+12+36} = \frac{16}{64} = \text{25%}\) \(\text{True Positive Rate} = \frac{6}{6+12} = \frac{6}{18} = \text{33%}\) |
\(\text{Positive Rate} = \frac{3+6}{3+6+6+21} = \frac{9}{36} = \text{25%}\) \(\text{True Positive Rate} = \frac{3}{3+6} = \frac{3}{9} = \text{33%}\) |
|||
Les groupes majoritaires et minoritaires présentent un taux de prédiction positif de 25%, qui respecte la parité démographique et un taux de vrais positifs (pourcentage d'exemples avec l'étiquette préférée qui sont correctement classée) de 33%, ce qui satisfait l'égalité des chances.
