Binning (که به آن سطل نیز میگویند) یک تکنیک مهندسی ویژگی است که زیرمجموعههای عددی مختلف را در سطلها یا سطلها گروهبندی میکند. در بسیاری از موارد، binning داده های عددی را به داده های طبقه ای تبدیل می کند. به عنوان مثال، یک ویژگی به نام X را در نظر بگیرید که کمترین مقدار آن 15 و بالاترین مقدار آن 425 است. با استفاده از binning، می توانید X با پنج bin زیر نشان دهید:
- بن 1: 15 تا 34
- Bin 2: 35 تا 117
- بن 3: 118 تا 279
- Bin 4: 280 تا 392
- بن 5: 393 تا 425
Bin 1 محدوده 15 تا 34 را در بر می گیرد، بنابراین هر مقدار X بین 15 و 34 به Bin 1 ختم می شود. مدلی که روی این bin ها آموزش داده شده است، هیچ واکنش متفاوتی به X مقادیر 17 و 29 نشان نمی دهد زیرا هر دو مقدار در Bin 1 هستند.
بردار ویژگی پنج bin را به صورت زیر نشان می دهد:
| شماره بن | محدوده | بردار ویژگی |
|---|---|---|
| 1 | 15-34 | [1.0، 0.0، 0.0، 0.0، 0.0] |
| 2 | 35-117 | [0.0، 1.0، 0.0، 0.0، 0.0] |
| 3 | 118-279 | [0.0، 0.0، 1.0، 0.0، 0.0] |
| 4 | 280-392 | [0.0، 0.0، 0.0، 1.0، 0.0] |
| 5 | 393-425 | [0.0، 0.0، 0.0، 0.0، 1.0] |
حتی اگر X یک ستون در مجموعه داده است، binning باعث می شود که یک مدل X به عنوان پنج ویژگی جداگانه در نظر بگیرد. بنابراین، مدل وزنهای جداگانهای را برای هر سطل یاد میگیرد.
هنگامی که یکی از شرایط زیر برآورده می شود، باینینگ جایگزین خوبی برای پوسته پوسته شدن یا بریدن است:
- رابطه خطی کلی بین ویژگی و برچسب ضعیف است یا وجود ندارد.
- زمانی که مقادیر ویژگی ها خوشه بندی می شوند.
با توجه به اینکه مدل در مثال قبلی با مقادیر 37 و 115 به طور یکسان رفتار می کند، Binning می تواند غیر منطقی به نظر برسد. اما زمانی که یک ویژگی بیشتر از خطی به نظر می رسد، ترکیب بندی روش بسیار بهتری برای نمایش داده ها است.
مثال بنینگ: تعداد خریداران در مقابل دما
فرض کنید در حال ایجاد مدلی هستید که تعداد خریداران را بر اساس دمای بیرون برای آن روز پیش بینی می کند. در اینجا نمودار دما در مقابل تعداد خریداران آمده است:

این طرح نشان میدهد، جای تعجب نیست که تعداد خریداران در زمانی که دما راحتتر بود، بالاترین میزان بود.
شما می توانید ویژگی را به صورت مقادیر خام نمایش دهید: دمای 35.0 در مجموعه داده، 35.0 در بردار ویژگی خواهد بود. آیا این بهترین ایده است؟
در طول آموزش، یک مدل رگرسیون خطی یک وزن واحد را برای هر ویژگی میآموزد. بنابراین، اگر دما به عنوان یک ویژگی منفرد نشان داده شود، دمای 35.0 پنج برابر تأثیر (یا یک پنجم تأثیر) در پیشبینی دمای 7.0 خواهد داشت. با این حال، نمودار واقعاً هیچ نوع رابطه خطی بین برچسب و مقدار ویژگی را نشان نمی دهد.
نمودار سه خوشه را در زیرمجموعه های زیر نشان می دهد:
- Bin 1 محدوده دمایی 4-11 است.
- Bin 2 محدوده دمایی 12-26 است.
- Bin 3 محدوده دمایی 27-36 است.
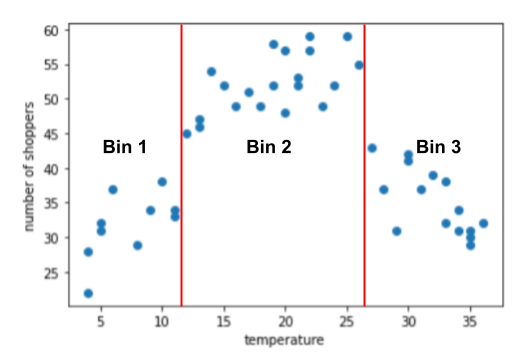
مدل وزن های جداگانه ای را برای هر سطل یاد می گیرد.
در حالی که امکان ایجاد بیش از سه سطل، حتی یک سطل جداگانه برای هر اندازه گیری دما وجود دارد، این اغلب به دلایل زیر ایده بدی است:
- یک مدل تنها زمانی می تواند ارتباط بین bin و برچسب را یاد بگیرد که نمونه های کافی در آن bin وجود داشته باشد. در مثال داده شده، هر یک از 3 سطل شامل حداقل 10 مثال است که ممکن است برای آموزش کافی باشد. با وجود 33 سطل جداگانه، هیچ یک از سطل ها شامل نمونه های کافی برای آموزش مدل نیستند.
- یک سطل جداگانه برای هر دما منجر به 33 ویژگی دمای جداگانه می شود. با این حال، معمولاً باید تعداد ویژگیهای یک مدل را به حداقل برسانید .
تمرین: درک خود را بررسی کنید
نمودار زیر میانگین قیمت خانه را برای هر 0.2 درجه عرض جغرافیایی برای کشور افسانه ای Freedonia نشان می دهد:

این نمودار یک الگوی غیر خطی بین ارزش اصلی و عرض جغرافیایی را نشان می دهد، بنابراین بعید است که نشان دادن عرض جغرافیایی به عنوان مقدار ممیز شناور به یک مدل کمک کند تا پیش بینی خوبی داشته باشد. شاید سطل کردن عرض های جغرافیایی ایده بهتری باشد؟
- 41.0 تا 41.8
- 42.0 تا 42.6
- 42.8 تا 43.4
- 43.6 تا 44.8
کوانتیل باکتینگ
سطل کوانتیل مرزهای سطلی را ایجاد می کند به طوری که تعداد نمونه ها در هر سطل دقیقاً یا تقریباً برابر است. کوانتیل سطل بیشتر نقاط پرت را پنهان می کند.
برای نشان دادن مشکلی که سطل چندک حل می کند، سطل های با فاصله مساوی را که در شکل زیر نشان داده شده اند، در نظر بگیرید، جایی که هر یک از ده سطل نشان دهنده یک دهانه دقیقاً 10000 دلار است. توجه داشته باشید که سطل از 0 تا 10000 شامل ده ها مثال است اما سطل از 50000 تا 60000 فقط شامل 5 مثال است. در نتیجه، این مدل نمونههای کافی برای آموزش در سطل 0 تا 10000 دارد، اما نمونههای کافی برای آموزش برای سطل 50000 تا 60000 وجود ندارد.

در مقابل، در شکل زیر از سطل چندکی برای تقسیم قیمت خودروها به سطلهایی با تعداد نمونههای تقریباً یکسان در هر سطل استفاده میشود. توجه داشته باشید که برخی از سطلها دامنه قیمتی باریکی را در بر میگیرند در حالی که برخی دیگر دامنه قیمتی بسیار وسیعی را در بر میگیرند.

