הוגנות: שוויון הזדמנויות

בקטע הקודם, הערכה הוגנת של מודל הקבלה שלנו שוויון דמוגרפי, על ידי השוואה של שיעורי ההסכמה הכוללים של שני הסוגים קבוצות דמוגרפיות.

לחלופין, נוכל להשוות את שיעורי הקבלה של מועמדים בקבוצת הרוב ובקבוצת המיעוט. אם שיעורי האישור לתלמידים מוסמכים בשתי הקבוצות הם שווי ערך, המודל מוצג שוויון הזדמנויות: תלמידים עם התווית המועדפת שלנו ('עומדים בדרישות להרשמה') מקבלים סיכוי להתקבל לתוכנית, בלי קשר לקבוצה הדמוגרפית שהם שייכים ל.

נחזור למאגר המועמדים מהקטע הקודם:

	קבוצת רוב	קבוצת מיעוט
עומד בדרישות	35	15
לא כשיר	45	5

נניח שמודל הקבלה מקבל 14 מועמדים מקבוצת הרוב ו-6 מועמדים מקבוצת מיעוט. ההחלטות שהמודל יצר שוויון הזדמנויות, כמו שיעור ההתקבלות לרוב המאושרים והמועמדים למיעוט שעומדים בדרישות הם 40%.

איור 4. פירוט של המועמדים שנדחו והמועמדים שהתקבלו, עם כל סטודנטים מוסמכים הן בקבוצות הרוב וגם בקבוצות המיעוט, מוצללות בצבע ירוק. מתוך 35 הסטודנטים בקבוצת הרוב, 14 היו התקבל. מתוך 15 הסטודנטים בקבוצת מיעוט מוסמכים, 6 היו התקבל. לכן שיעור ההצטרפות לשתי הקבוצות הוא 40% עבור סטודנטים מוסמכים.

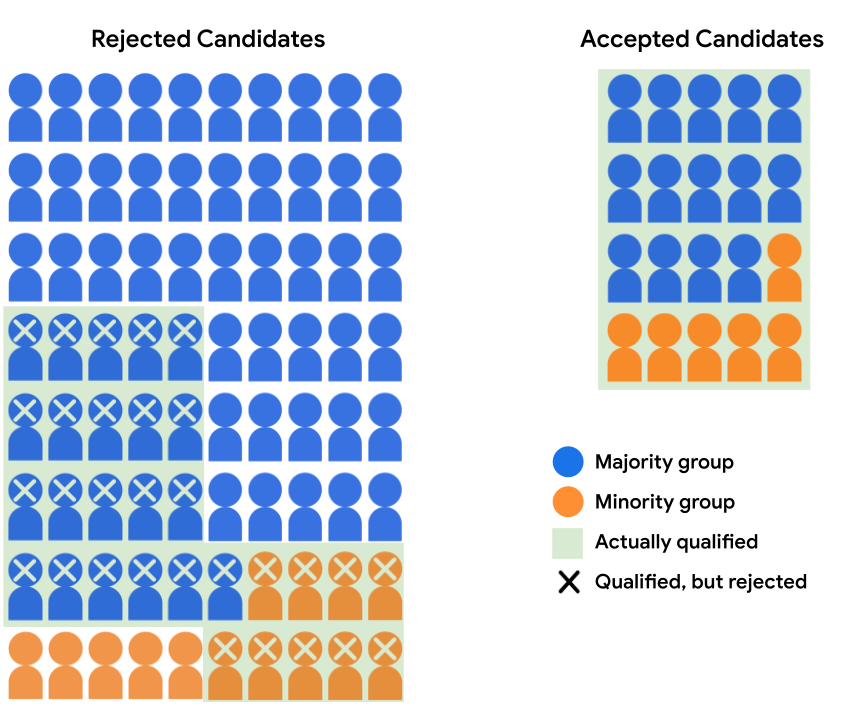
בטבלה הבאה מוצגים הערכים של מספרי הטלפון שתומכים למילות מפתח שנדחו ואושרו המועמדים השונים, כפי שמתואר באיור 4.

	קבוצת רוב		קבוצת מיעוט
	אושרו	נדחה	אושרו	נדחה
עומד בדרישות	14	21	6	9
לא כשיר	0	45	0	5

יתרונות וחסרונות

היתרון המרכזי של שוויון הזדמנויות הוא שהוא מאפשר למודל היחס בין חיזויים חיוביים לשליליים, שישתנו בין קבוצות דמוגרפיות שונות, בתנאי שהמודל מוצלח באותה מידה בחיזוי התווית המועדפת ('עומדת בדרישות כניסה') לשתי הקבוצות.

תחזיות המודל באיור 4 לא תואמות לשוויון הדמוגרפי, לתלמיד בקבוצת הרוב יש סיכוי של 17.5% להתקבל, לתלמיד בקבוצת המיעוט יש סיכוי של 30% להתקבל. אבל, לפעמים יש סיכוי של 40% להתקבל לסטודנט מוסמך, בלי קשר הקבוצה שאליה הם שייכים, שניתן לטעון שתוצאה הוגנת יותר במקרה זה של מודל ספציפי.

אחד החסרונות של שוויון הזדמנויות הוא שהוא נועד לשימוש במקרים שבהם יש תווית מועדפת ברורה. אם זה חשוב באותה מידה שהמודל חוזים גם את הסיווג החיובי ('כשיר לזכאות לדמי כניסה') ו- אולי כדאי להשתמש במקום זאת במדד שוויון סיכויים, שאוכף שיעורי הצלחה זהים עבור שתי התוויות.

חיסרון נוסף של שוויון הזדמנויות הוא ההערכה של הוגנות באמצעות השוואת שיעורי שגיאות באופן מצטבר עבור קבוצות דמוגרפיות, שעשוי לא תמיד שימושי. לדוגמה, אם מערך הנתונים של מודל הכניסה לא היה מאפיין של demographic_group, לפרט את שיעורי הקבלה למועמדים המתאימים לרוב ומיעוט ולהשוות ביניהם כדי לראות אם שוויון ההזדמנויות מרוצה.

בקטע הבא נבחן מדד אחר של הוגנות, הוגנות, ניתן להשתמש בה בתרחישים שבהם נתונים דמוגרפיים לא קיימים בכל הדוגמאות.

תרגיל: בדקו את ההבנה שלכם

True או False: לא ניתן להשתמש במודל סיווג בינארי כדי לספק שוויון דמוגרפי וגם שוויון הזדמנויות אותה קבוצת חיזויים.

נכון

ייתכן שהתחזיות של המודל יענו על שתי קבוצות דמוגרפיות שוויון הזדמנויות ושוויון הזדמנויות. נסו לחשוב על רעיון שבו שני המדדים מתקיימים, ואז לבחור כדי לקרוא את ההסבר שלנו.

לא נכון

ייתכן שהתחזיות של המודל יענו על שתי קבוצות דמוגרפיות שוויון הזדמנויות ושוויון הזדמנויות.

לדוגמה, נניח שהמסווג הבינארי (התווית המועדפת עליו הוא המחלקה החיובית) מוערך על סמך 100 דוגמאות, ותוצאות במטריצות הבלבול הבאות, בחלוקה לפי קבוצה דמוגרפית (רוב ומיעוט):

	קבוצת רוב		קבוצת מיעוט
	צפי חיובי	ערך שלילי חזוי	צפי חיובי	ערך שלילי חזוי
חיובי בפועל	6	12	3	6
שלילית בפועל	10	36	6	21
	\(\text{Positive Rate} = \frac{6+10}{6+10+12+36} = \frac{16}{64} = \text{25%}\) \(\text{True Positive Rate} = \frac{6}{6+12} = \frac{6}{18} = \text{33%}\)		\(\text{Positive Rate} = \frac{3+6}{3+6+6+21} = \frac{9}{36} = \text{25%}\) \(\text{True Positive Rate} = \frac{3}{3+6} = \frac{3}{9} = \text{33%}\)

גם לקבוצת הרוב וגם לקבוצות המיעוט יש שיעור חיזוי חיובי של 25%, שוויון דמוגרפי מתאים ושיעור חיובי אמיתי (אחוז הדוגמאות עם התווית המועדפת שסווג בצורה נכונה) של 33%, תוך הבטחת שוויון הזדמנויות.

מונחי מפתח:

• הטיה (אתיקה/הגינות)
• שוויון הזדמנויות
• סיכויים שווים