Cette section aborde les trois questions suivantes :
- Quelle est la différence entre les ensembles de données équilibrés et ceux qui ne le sont pas ?
- Pourquoi est-il difficile d'entraîner un ensemble de données déséquilibré ?
- Comment surmonter les problèmes liés à l'entraînement d'ensembles de données déséquilibrés ?
Ensembles de données équilibrés par classe et ensembles de données avec déséquilibre des classes
Prenons l'exemple d'un ensemble de données contenant un libellé catégoriel dont la valeur correspond à la classe positive ou négative. Dans un ensemble de données équilibré, le nombre de classes positives et de classes négatives est à peu près égal. Par exemple, un ensemble de données contenant 235 classes positives et 247 classes négatives est un ensemble de données équilibré.
Dans un ensemble de données avec déséquilibre des classes, une étiquette est beaucoup plus fréquente que l'autre. Dans le monde réel, les ensembles de données avec déséquilibre des classes sont beaucoup plus courants que ceux avec équilibre des classes. Par exemple, dans un ensemble de données de transactions par carte de crédit, les achats frauduleux peuvent représenter moins de 0,1 % des exemples. De même, dans un ensemble de données de diagnostic médical, le nombre de patients atteints d'un virus rare peut représenter moins de 0,01 % du nombre total d'exemples. Dans un ensemble de données avec déséquilibre des classes :
- L'étiquette la plus courante est appelée classe majoritaire.
- L'étiquette la moins courante est appelée classe minoritaire.
Difficulté d'entraîner des ensembles de données avec un déséquilibre des classes important
L'entraînement vise à créer un modèle qui distingue correctement la classe positive de la classe négative. Pour ce faire, les lots doivent comporter un nombre suffisant de classes positives et négatives. Cela ne pose pas de problème lors de l'entraînement sur un ensemble de données légèrement déséquilibré, car même les petits lots contiennent généralement suffisamment d'exemples de la classe positive et de la classe négative. Toutefois, un ensemble de données présentant un déséquilibre de classe important peut ne pas contenir suffisamment d'exemples de classe minoritaire pour un entraînement approprié.
Par exemple, prenons l'ensemble de données avec déséquilibre des classes illustré à la figure 6, dans lequel :
- 200 étiquettes appartiennent à la classe majoritaire.
- Deux libellés appartiennent à la classe minoritaire.
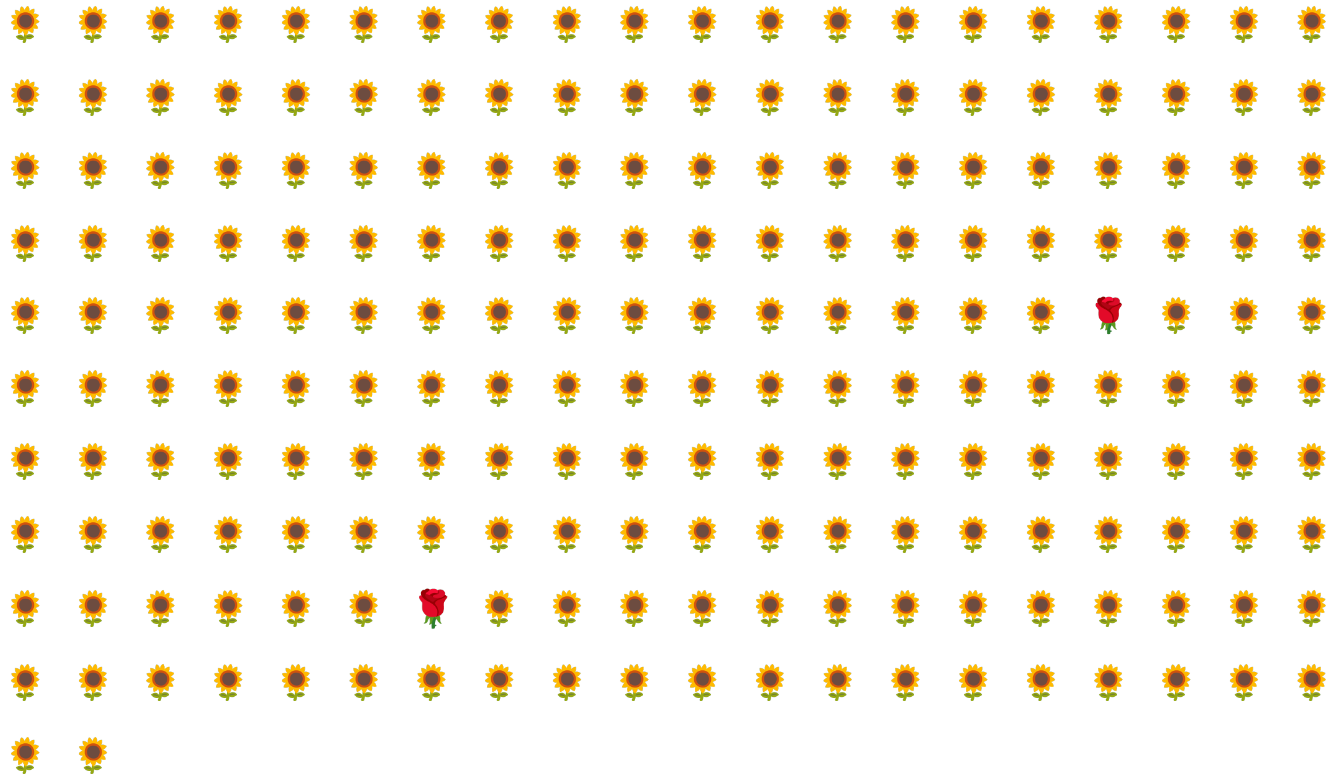
Si la taille de lot est de 20, la plupart des lots ne contiendront aucun exemple de la classe minoritaire. Si la taille du lot est de 100, chaque lot ne contiendra en moyenne qu'un seul exemple de classe minoritaire, ce qui est insuffisant pour un entraînement approprié. Même une taille de lot beaucoup plus importante donnera toujours une proportion aussi déséquilibrée que le modèle risque de ne pas s'entraîner correctement.
Entraîner un ensemble de données avec déséquilibre des classes
Lors de l'entraînement, un modèle doit apprendre deux choses :
- À quoi ressemble chaque classe ? Autrement dit, à quelle classe correspondent les valeurs des caractéristiques ?
- La fréquence de chaque classe, c'est-à-dire la distribution relative des classes.
L'entraînement standard confond ces deux objectifs. En revanche, la technique en deux étapes suivante, appelée sous-échantillonnage et surpondération de la classe majoritaire, sépare ces deux objectifs, ce qui permet au modèle d'atteindre les deux objectifs.
Étape 1 : Sous-échantillonner la classe majoritaire
Le sous-échantillonnage consiste à entraîner le modèle sur un pourcentage excessivement faible d'exemples de la classe majoritaire. En d'autres termes, vous forcez artificiellement un ensemble de données déséquilibrées en termes de classes à devenir un peu plus équilibré en omettant de nombreux exemples de la classe majoritaire de l'entraînement. Le sous-échantillonnage augmente considérablement la probabilité que chaque lot contienne suffisamment d'exemples de la classe minoritaire pour entraîner le modèle correctement et efficacement.
Par exemple, l'ensemble de données déséquilibré en termes de classes présenté sur la figure 6 se compose de 99 % d'exemples de la classe majoritaire et de 1 % d'exemples de la classe minoritaire. Le sous-échantillonnage de la classe majoritaire par un facteur 25 crée artificiellement un ensemble d'entraînement plus équilibré (80 % de classe majoritaire et 20 % de classe minoritaire), comme suggéré dans la figure 7 :

Étape 2 : Augmenter le poids de la classe sous-échantillonnée
Le sous-échantillonnage introduit un biais de prédiction en montrant au modèle un monde artificiel où les classes sont plus équilibrées que dans le monde réel. Pour corriger ce biais, vous devez "surpondérer" les classes majoritaires par le facteur de sous-échantillonnage. La surpondération signifie que la perte sur un exemple de classe majoritaire est traitée plus sévèrement que la perte sur un exemple de classe minoritaire.
Par exemple, nous avons sous-échantillonné la classe majoritaire par un facteur de 25. Nous devons donc surpondérer la classe majoritaire par un facteur de 25. Autrement dit, lorsque le modèle prédit à tort la classe majoritaire, traitez la perte comme s'il s'agissait de 25 erreurs (multipliez la perte habituelle par 25).

Dans quelle mesure devez-vous sous-échantillonner et surpondérer pour rééquilibrer votre ensemble de données ? Pour déterminer la réponse, vous devez tester différents facteurs de sous-échantillonnage et de surpondération, comme vous le feriez avec d'autres hyperparamètres.
Avantages de cette technique
Le sous-échantillonnage et la surpondération de la classe majoritaire présentent les avantages suivants :
- Meilleur modèle : le modèle résultant "connaît" les deux éléments suivants :
- Le lien entre les caractéristiques et les libellés
- La distribution réelle des classes
- Convergence plus rapide : pendant l'entraînement, le modèle voit plus souvent la classe minoritaire, ce qui l'aide à converger plus rapidement.