W tej sekcji odpowiemy na te 3 pytania:
- Czym różnią się zbiory danych z równowagą klas od zbiorów danych z nierównowagą klas?
- Dlaczego trenowanie modelu na niezrównoważonym zbiorze danych jest trudne?
- Jak można rozwiązać problemy związane z trenowaniem niezrównoważonych zbiorów danych?
Zbiory danych z równowagą klas a zbiory danych z nierównowagą klas
Rozważ zbiór danych zawierający etykietę kategorialną, której wartość jest klasą pozytywną lub negatywną. W zbiorze danych o zrównoważonych klasach liczba klas pozytywnych i klas negatywnych jest mniej więcej równa. Na przykład zbiór danych zawierający 235 klas pozytywnych i 247 klas negatywnych jest zrównoważony.
W zbiorze danych z nierównowagą klas jedna etykieta występuje znacznie częściej niż druga. W rzeczywistości zbiory danych z nierównowagą klas są znacznie częstsze niż zbiory danych z równowagą klas. Na przykład w zbiorze danych transakcji kartą kredytową oszukańcze zakupy mogą stanowić mniej niż 0,1% przykładów. Podobnie w zbiorze danych dotyczących diagnoz medycznych liczba pacjentów z rzadkim wirusem może stanowić mniej niż 0,01% wszystkich przykładów. W zbiorze danych z niezrównoważonymi klasami:
- Etykieta częstsza jest nazywana klasą większościową.
- Rzadziej wybierana etykieta jest nazywana klasą mniejszościową.
Trudności związane z trenowaniem zbiorów danych z dużą nierównowagą klas
Trenowanie ma na celu utworzenie modelu, który skutecznie odróżnia klasę pozytywną od negatywnej. W tym celu partie muszą zawierać wystarczającą liczbę zarówno klas pozytywnych, jak i negatywnych. Nie stanowi to problemu podczas trenowania na zbiorze danych z niewielką nierównowagą klas, ponieważ nawet małe partie zwykle zawierają wystarczającą liczbę przykładów zarówno klasy pozytywnej, jak i negatywnej. Jednak zbiór danych z dużą nierównowagą klas może nie zawierać wystarczającej liczby przykładów klasy mniejszościowej do prawidłowego trenowania.
Rozważmy na przykład zbiór danych z nierównomiernym rozkładem klas przedstawiony na rysunku 6, w którym:
- 200 etykiet należy do klasy większościowej.
- 2 etykiety należą do klasy mniejszościowej.
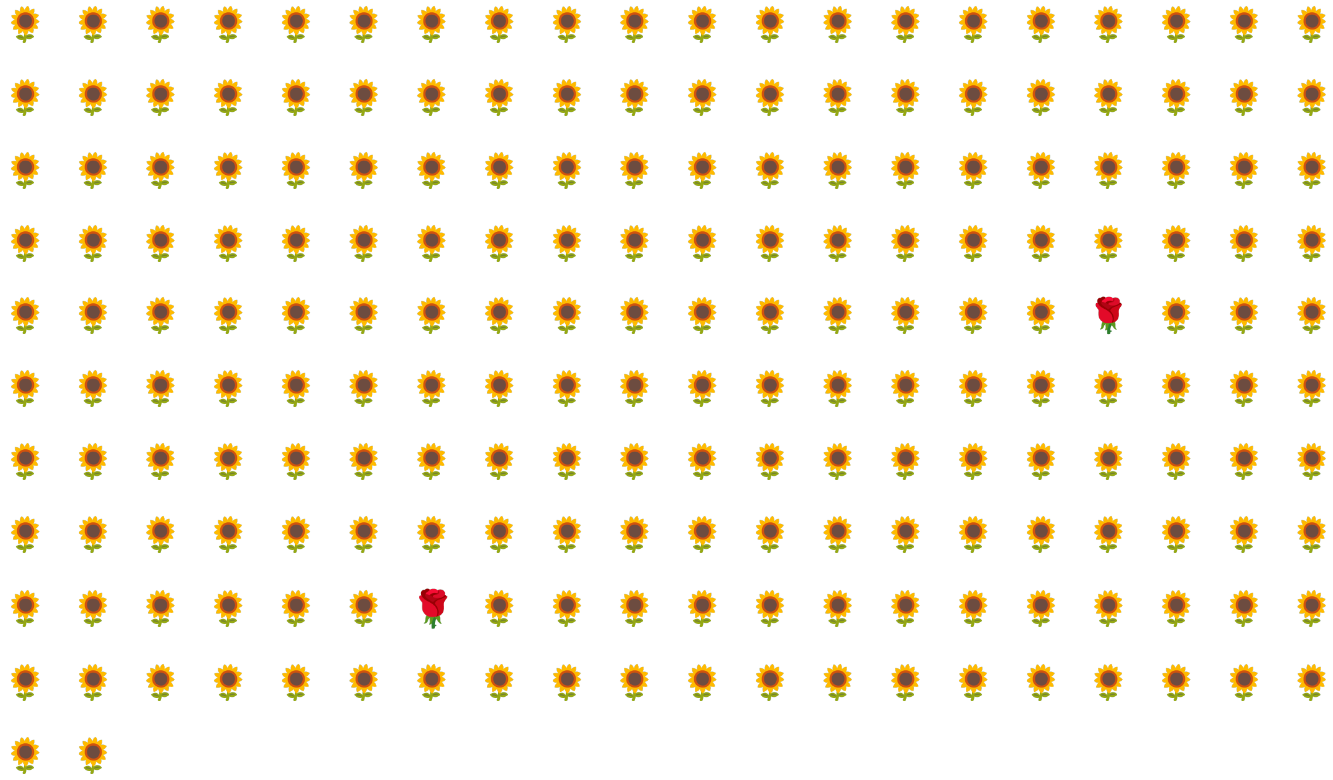
Jeśli rozmiar partii wynosi 20, większość partii nie będzie zawierać żadnych przykładów klasy mniejszościowej. Jeśli rozmiar partii wynosi 100, każda partia będzie zawierać średnio tylko 1 przykład klasy mniejszościowej, co jest niewystarczające do prawidłowego trenowania. Nawet znacznie większy rozmiar partii nadal będzie dawać tak niezrównoważoną proporcję, że model może nie zostać prawidłowo wytrenowany.
Trenowanie zbioru danych z nierównowagą klas
Podczas trenowania model powinien nauczyć się dwóch rzeczy:
- Jak wygląda każda klasa, czyli jakie wartości cech odpowiadają jakiej klasie.
- Jak często występuje każda klasa, czyli jaki jest względny rozkład klas?
Standardowe trenowanie łączy te 2 cele. Natomiast poniższa 2-etapowa technika o nazwie downsampling and upweighting the majority class (zmniejszanie próbkowania i zwiększanie wagi klasy większościowej) rozdziela te 2 cele, dzięki czemu model może osiągnąć oba z nich.
Krok 1. Zmniejsz próbę klasy większościowej
Zmniejszanie liczby próbek oznacza trenowanie na nieproporcjonalnie małym odsetku przykładów klasy większościowej. Oznacza to, że sztucznie wymuszasz, aby zbiór danych z nierównowagą klas stał się nieco bardziej zrównoważony, pomijając w procesie trenowania wiele przykładów klasy większościowej. Downsampling znacznie zwiększa prawdopodobieństwo, że każdy pakiet zawiera wystarczającą liczbę przykładów klasy mniejszościowej, aby prawidłowo i skutecznie wytrenować model.
Na przykład zbiór danych z niezrównoważonymi klasami przedstawiony na rysunku 6 składa się z 99% przykładów klasy większościowej i 1% przykładów klasy mniejszościowej. Zmniejszenie próbkowania większościowej klasy o współczynnik 25 sztucznie tworzy bardziej zrównoważony zbiór treningowy (80% klasy większościowej i 20% klasy mniejszościowej), co przedstawiono na rysunku 7:

Krok 2. Zwiększ wagę klasy z próbkowaniem w dół
Downsampling wprowadza błąd prognozy, ponieważ pokazuje modelowi sztuczny świat, w którym klasy są bardziej zrównoważone niż w rzeczywistości. Aby skorygować to odchylenie, musisz „zwiększyć wagę” klas większości o współczynnik, o który zmniejszyłeś próbę. Zwiększanie wagi oznacza traktowanie straty w przypadku przykładu z klasy większościowej surowiej niż straty w przypadku przykładu z klasy mniejszościowej.
Na przykład zmniejszyliśmy próbę klasy większości 25-krotnie, więc musimy zwiększyć jej wagę 25-krotnie. Oznacza to, że gdy model błędnie przewiduje klasę większościową, traktuj stratę tak, jakby było 25 błędów (pomnóż zwykłą stratę przez 25).

O ile należy zmniejszyć próbę i zwiększyć wagę, aby przywrócić równowagę w zbiorze danych? Aby znaleźć odpowiedź, eksperymentuj z różnymi współczynnikami próbkowania w dół i zwiększania wagi, tak jak eksperymentujesz z innymi hiperparametrami.
Zalety tej techniki
Zmniejszenie próbkowania i zwiększenie wagi klasy większości przynosi następujące korzyści:
- Lepszy model: wynikowy model „wie” o obu tych kwestiach:
- związek między cechami a etykietami,
- rzeczywisty rozkład klas,
- Szybsza konwergencja: podczas trenowania model częściej widzi klasę mniejszościową, co pomaga mu szybciej się dostosować.