コンピュータ サイエンスにおける多くの問題は、ノードとノード間のリンクで構成されるグラフで表すことができます。たとえば、鉄道システムなどのネットワークを介して商品や資材を輸送する場合に、ネットワーク フローの問題があります。
ノードが都市で、円弧がノード間の線であるグラフでネットワーク フローを表すことができます。（これらの特徴は、パイプのネットワークに流れる水の性質に似ているため「フロー」と呼ばれます）。
ネットワーク フローの主な制約事項は、各アークに容量（アーク全体で一定時間内に転送できる最大量）があることです。
最大フローの問題は、容量の制約に応じて、ネットワーク内のすべてのアークで転送できる最大合計量を決定することです。
この問題を最初に研究したのは、1930 年代にロシアの数学者 A.N. Tolstoi でした。以下の地図は、最大のフローを求める実際の鉄道網を示しています。
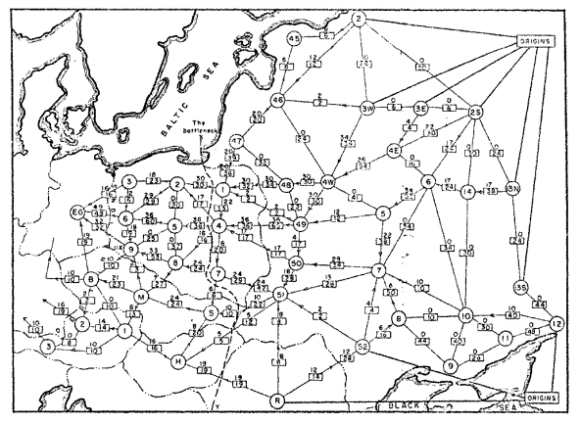
OR-Tools には、グラフ ライブラリのネットワーク フローの問題に対して、いくつかのソルバーが用意されています。
以降のセクションでは、ネットワーク フローの問題の例と、解決方法について説明します。