网络流
计算机科学中的许多问题都可以由一个包含节点及其间的链接的图表来表示。例如，涉及网络（例如铁路系统）运输商品或材料的网络流问题。
您可以通过一个图来表示网络流，该图中的节点是城市，而弧线是它们之间的铁轨。（之所以称为“流”，是因为它们的特性与流经管道网络的水类似。）
网络流中的一个关键限制是，每个弧线都有一个容量，即可在固定时间段内跨弧传送的最大容量。
最大流量问题用于确定在流量限制范围内可跨网络所有弧线传输的最大总量。
第一个研究这个问题的人是 20 世纪 30 年代的俄罗斯数学家托尔斯泰。下面的地图显示了他希望达到最大交通流的实际铁路网络。
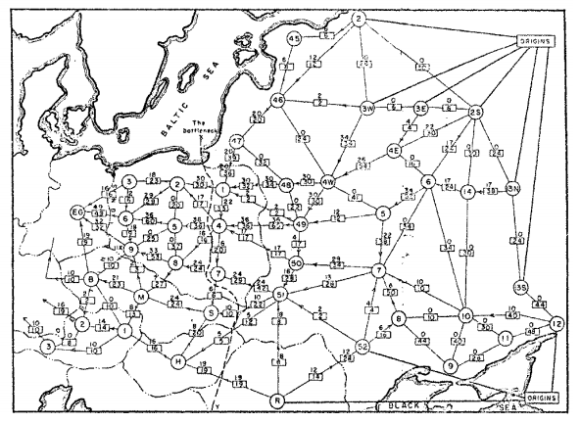
OR-Tools 在其图库中为网络流问题提供了多个求解器。
以下部分提供了网络流问题示例，并说明了如何解决这些问题：
如未另行说明，那么本页面中的内容已根据知识共享署名 4.0 许可获得了许可，并且代码示例已根据 Apache 2.0 许可获得了许可。有关详情，请参阅 Google 开发者网站政策。Java 是 Oracle 和/或其关联公司的注册商标。
最后更新时间 (UTC)：2024-08-09。
[null,null,["最后更新时间 (UTC)：2024-08-09。"],[[["Network flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits."],["The maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints."],["OR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows."],["Example applications of network flows include assignments with individual workers or teams, solvable using OR-Tools."]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"]]
