Nhiều vấn đề trong khoa học máy tính có thể được biểu thị bằng một biểu đồ bao gồm các nút và liên kết giữa chúng. Ví dụ như sự cố luồng mạng, liên quan đến việc vận chuyển hàng hoá hoặc vật liệu trên mạng, chẳng hạn như hệ thống đường sắt.
Bạn có thể biểu diễn luồng mạng bằng một biểu đồ có các nút là thành phố và có các đường thẳng là các đường ray ở giữa. (Chúng được gọi là luồng vì các thuộc tính của chúng giống với thuộc tính của nước chảy qua một mạng lưới đường ống.)
Một hạn chế chính trong các luồng mạng là mỗi vòng cung có một dung lượng — số lượng tối đa có thể được truyền qua vòng cung trong một khoảng thời gian cố định.
Vấn đề tối đa về luồng là xác định tổng số lượng tối đa có thể truyền tải qua tất cả các vòng cung trong mạng, tuỳ thuộc vào các hạn chế về dung lượng.
Người đầu tiên nghiên cứu vấn đề này là nhà toán học người Nga A.N. Tolstoi, vào những năm 1930. Bản đồ dưới đây cho thấy mạng lưới đường sắt thực tế mà anh muốn tìm một lưu lượng tối đa.
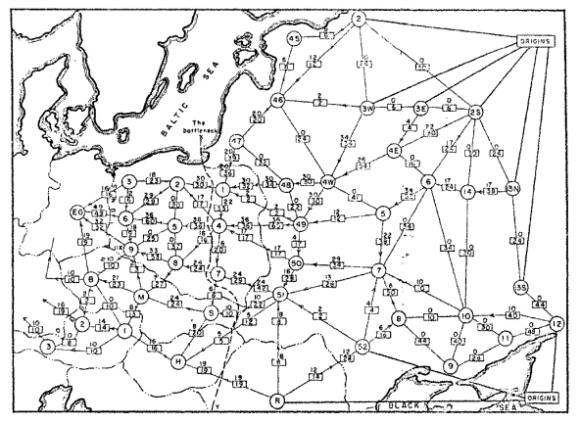
OR-Tools cung cấp một số giải pháp cho các vấn đề về luồng mạng trong thư viện graph của biểu đồ đó.
Các phần sau đây trình bày ví dụ về các vấn đề về luồng mạng và hướng dẫn cách giải quyết:
[null,null,["Cập nhật lần gần đây nhất: 2024-08-09 UTC."],[[["Network flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits."],["The maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints."],["OR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows."],["Example applications of network flows include assignments with individual workers or teams, solvable using OR-Tools."]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"]]
