網路流程
電腦科學中的許多問題可以用圖表組成，這些節點由節點及其節點之間的連結組成。例如「網路流程」問題，這類問題涉及網路 (例如鐵道系統) 傳輸物品或材料。
您可以使用一個節點來呈現網路流程，該節點的節點是城市，其弧形是節點之間的鐵線。(這些屬性稱為「資料流」，因為其屬性與透過管線網路流入的水類似)。
網路流程中的一個關鍵限制就是，每個弧線都有「容量」，也就是在固定時間範圍內，跨弧的傳輸量上限。
「最大流程問題」是用於決定網路中所有弧形的傳輸上限，取決於容量限制。
第一個研究這個問題的人是 1930 年代的俄羅斯數學家 A.N. Tolstoi下方地圖顯示他想要尋找最大流程的實際鐵路網路。
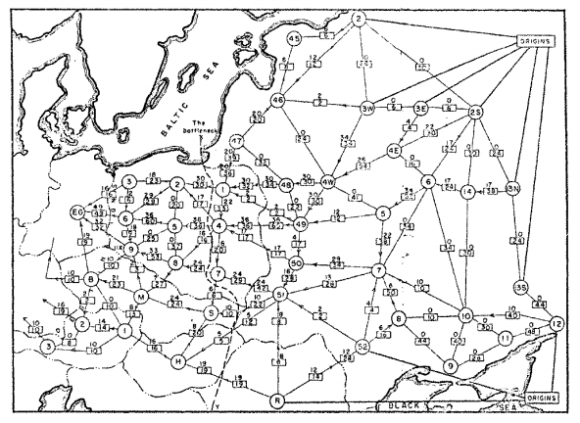
OR-Tools 在其 graph 程式庫中為網路流程問題提供了數個解題工具。
以下各節提供了網路流程問題的實例，並示範如何解決這些問題：
除非另有註明，否則本頁面中的內容是採用創用 CC 姓名標示 4.0 授權，程式碼範例則為阿帕契 2.0 授權。詳情請參閱《Google Developers 網站政策》。Java 是 Oracle 和/或其關聯企業的註冊商標。
上次更新時間：2024-08-09 (世界標準時間)。
[null,null,["上次更新時間：2024-08-09 (世界標準時間)。"],[[["Network flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits."],["The maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints."],["OR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows."],["Example applications of network flows include assignments with individual workers or teams, solvable using OR-Tools."]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"]]
