Alur Jaringan
Banyak masalah dalam ilmu komputer dapat direpresentasikan oleh grafik yang terdiri dari
node dan keterkaitan di antara keduanya. Contohnya adalah masalah aliran jaringan, yang
mengangkut barang atau material di seluruh jaringan, seperti sistem kereta api.
Anda dapat merepresentasikan alur jaringan dengan grafik yang node-nya adalah kota dan busurnya
berbentuk garis rel di antara keduanya. (Disebut flow karena propertinya
mirip dengan air yang mengalir melalui jaringan pipa.)
Batasan utama dalam alur jaringan adalah bahwa setiap busur memiliki kapasitas —
jumlah maksimum yang dapat diangkut melintasi busur dalam jangka
waktu tetap.
Masalah flow maksimum adalah menentukan jumlah total maksimum yang dapat
diangkut di semua busur dalam jaringan, yang tunduk pada batasan kapasitas.
Orang pertama yang mempelajari masalah ini adalah ahli matematika Rusia, A.N.
Tolstoi, pada tahun 1930-an. Peta di bawah ini menunjukkan jaringan kereta api sebenarnya yang ingin ditemukan alur maksimumnya.
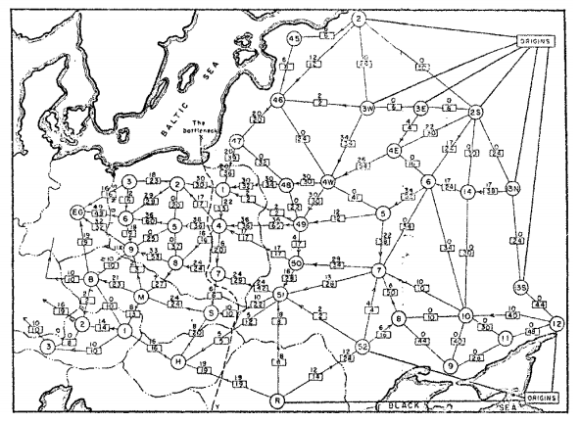
OR-Tools menyediakan beberapa pemecah masalah untuk masalah aliran jaringan dalam
library grafik-nya.
Bagian berikut menampilkan contoh masalah alur jaringan dan menunjukkan cara
menyelesaikannya:
Kecuali dinyatakan lain, konten di halaman ini dilisensikan berdasarkan Lisensi Creative Commons Attribution 4.0, sedangkan contoh kode dilisensikan berdasarkan Lisensi Apache 2.0. Untuk mengetahui informasi selengkapnya, lihat Kebijakan Situs Google Developers. Java adalah merek dagang terdaftar dari Oracle dan/atau afiliasinya.
Terakhir diperbarui pada 2024-08-09 UTC.
[null,null,["Terakhir diperbarui pada 2024-08-09 UTC."],[[["Network flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits."],["The maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints."],["OR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows."],["Example applications of network flows include assignments with individual workers or teams, solvable using OR-Tools."]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"]]
