네트워크 흐름
컬렉션을 사용해 정리하기
내 환경설정을 기준으로 콘텐츠를 저장하고 분류하세요.
컴퓨터 공학의 많은 문제는 노드와 노드 간 링크로 구성된 그래프로 나타낼 수 있습니다. 예를 들어, 철도 시스템과 같이 네트워크를 통해 상품이나 자재를 운송하는 것과 관련된 네트워크 흐름 문제가 있습니다.
노드가 도시이고 그 사이의 호가 선로인 그래프로 네트워크 흐름을 나타낼 수 있습니다. 이러한 속성을 파이프라고 하는데, 이는 파이프 네트워크를 통해 흐르는 물과 속성이 유사하기 때문입니다.
네트워크 흐름의 주요 제약조건은 각 원에 용량(고정 기간 동안 호를 통해 전송할 수 있는 최대 금액)이 있다는 점입니다.
최대 흐름 문제는 용량 제약에 따라 네트워크의 모든 원호에 걸쳐 전송 가능한 최대 총량을 결정하는 것입니다.
이 문제를 연구한 첫 번째 사람은 1930년대 러시아의 수학자 A.N. 톨스토이였습니다. 아래 지도는 최대 통행량을 찾고자 했던 실제 철도망을 보여줍니다.
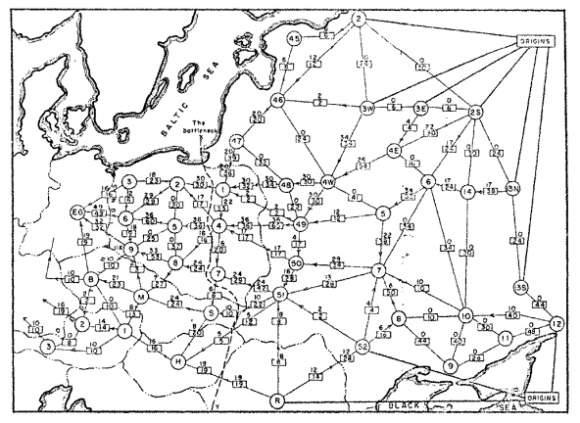
OR-도구는 그래프 라이브러리의 네트워크 흐름 문제를 위한 여러 솔버를 제공합니다.
다음 섹션에서는 네트워크 흐름 문제의 예와 해결 방법을 보여줍니다.
달리 명시되지 않는 한 이 페이지의 콘텐츠에는 Creative Commons Attribution 4.0 라이선스에 따라 라이선스가 부여되며, 코드 샘플에는 Apache 2.0 라이선스에 따라 라이선스가 부여됩니다. 자세한 내용은 Google Developers 사이트 정책을 참조하세요. 자바는 Oracle 및/또는 Oracle 계열사의 등록 상표입니다.
최종 업데이트: 2024-08-09(UTC)
[null,null,["최종 업데이트: 2024-08-09(UTC)"],[[["\u003cp\u003eNetwork flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits.\u003c/p\u003e\n"],["\u003cp\u003eThe maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints.\u003c/p\u003e\n"],["\u003cp\u003eOR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows.\u003c/p\u003e\n"],["\u003cp\u003eExample applications of network flows include assignments with individual workers or teams, solvable using OR-Tools.\u003c/p\u003e\n"]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"],null,["# Network Flows\n\nMany problems in computer science can be represented by a graph consisting of\nnodes and links between them. Examples are **network flow** problems, which\ninvolve transporting goods or material across a network, such as a railway system.\n\nYou can represent a network flow by a graph whose nodes are cities and whose\narcs are rail lines between them. (They're called **flows** because their\nproperties are similar to those of water flowing through a network of pipes.)\n\nA key constraint in network flows is that each arc has a **capacity** ---\nthe maximum amount that can be transported across the arc in a fixed period of\ntime.\n\nThe **maximum flow problem** is to determine the maximum total amount that can\nbe transported across all arcs in the network, subject to the capacity\nconstraints.\n\nThe first person to study this problem was the Russian mathematician A.N.\nTolstoi, in the 1930s. The map below shows the actual railway network for which\nhe wanted to find a maximum flow.\n\nOR-Tools provides several solvers for network flow problems in its\n[graph](/optimization/reference/graph) libraries.\n\nThe following sections present examples of network flow problems and show how to\nsolve them:\n\n- [Maximum Flows](/optimization/flow/maxflow)\n- [Minimum Cost Flows](/optimization/flow/mincostflow)\n- [Assignment as a Minimum Cost Flows](/optimization/flow/assignment_min_cost_flow#example)\n- [Assignment with Teams of Workers](/optimization/flow/assignment_min_cost_flow#teams-workers)"]]
