Przepływy sieciowe
Zadbaj o dobrą organizację dzięki kolekcji
Zapisuj i kategoryzuj treści zgodnie ze swoimi preferencjami.
Wiele problemów informatycznych może mieć postać wykresu składającego się z węzłów i linków. Przykładem mogą tu być problemy z przepływem sieci polegające na transportowaniu towarów lub materiałów w sieci, np. w systemie kolejowym.
Możesz przedstawić przepływ danych na wykresie, którego węzły są miastami i których łuki tworzą linie kolejowe. Są to tzw. przepływy, ponieważ ich właściwości są podobne do właściwości przepływającej przez sieć rur.
Głównym ograniczeniem w przepływach sieci jest to, że każdy z nich ma pojemność, czyli maksymalną ilość, jaką można przenieść, wykorzystując do tego określony przedział czasu.
Problem z maksymalnym przebiegiem przepływu określa maksymalną łączną ilość ruchu, jaką można przenieść we wszystkich łukach sieci, z uwzględnieniem ograniczeń pojemności.
Pierwszą osobą, która badała ten problem, był rosyjski matematyk A.N. Tolstoi. Na poniższej mapie przedstawiliśmy rzeczywistą sieć kolejową, dla której chcieliśmy znaleźć maksymalną prędkość.
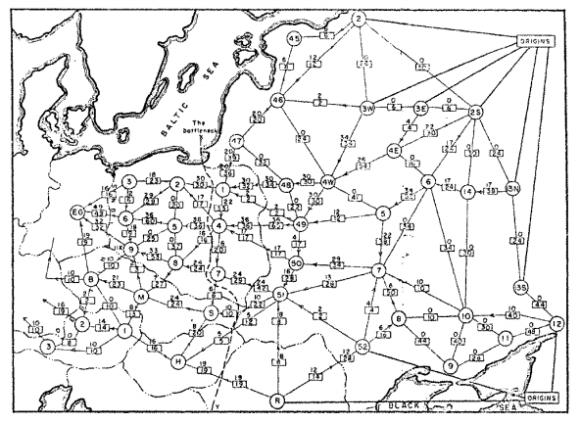
Narzędzie OR-Tools zawiera kilka rozwiązań problemów z przepływem sieci w jego bibliotekach graph.
Poniżej znajdziesz przykłady problemów z przepływem sieci oraz sposoby ich rozwiązywania:
O ile nie stwierdzono inaczej, treść tej strony jest objęta licencją Creative Commons – uznanie autorstwa 4.0, a fragmenty kodu są dostępne na licencji Apache 2.0. Szczegółowe informacje na ten temat zawierają zasady dotyczące witryny Google Developers. Java jest zastrzeżonym znakiem towarowym firmy Oracle i jej podmiotów stowarzyszonych.
Ostatnia aktualizacja: 2024-08-09 UTC.
[null,null,["Ostatnia aktualizacja: 2024-08-09 UTC."],[[["\u003cp\u003eNetwork flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits.\u003c/p\u003e\n"],["\u003cp\u003eThe maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints.\u003c/p\u003e\n"],["\u003cp\u003eOR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows.\u003c/p\u003e\n"],["\u003cp\u003eExample applications of network flows include assignments with individual workers or teams, solvable using OR-Tools.\u003c/p\u003e\n"]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"],null,["# Network Flows\n\nMany problems in computer science can be represented by a graph consisting of\nnodes and links between them. Examples are **network flow** problems, which\ninvolve transporting goods or material across a network, such as a railway system.\n\nYou can represent a network flow by a graph whose nodes are cities and whose\narcs are rail lines between them. (They're called **flows** because their\nproperties are similar to those of water flowing through a network of pipes.)\n\nA key constraint in network flows is that each arc has a **capacity** ---\nthe maximum amount that can be transported across the arc in a fixed period of\ntime.\n\nThe **maximum flow problem** is to determine the maximum total amount that can\nbe transported across all arcs in the network, subject to the capacity\nconstraints.\n\nThe first person to study this problem was the Russian mathematician A.N.\nTolstoi, in the 1930s. The map below shows the actual railway network for which\nhe wanted to find a maximum flow.\n\nOR-Tools provides several solvers for network flow problems in its\n[graph](/optimization/reference/graph) libraries.\n\nThe following sections present examples of network flow problems and show how to\nsolve them:\n\n- [Maximum Flows](/optimization/flow/maxflow)\n- [Minimum Cost Flows](/optimization/flow/mincostflow)\n- [Assignment as a Minimum Cost Flows](/optimization/flow/assignment_min_cost_flow#example)\n- [Assignment with Teams of Workers](/optimization/flow/assignment_min_cost_flow#teams-workers)"]]
