Bagian berikut menampilkan contoh masalah LP dan menunjukkan cara menyelesaikannya. Inilah masalahnya:
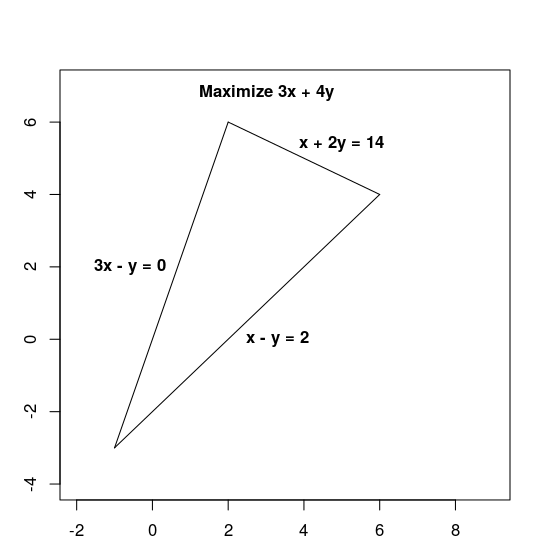
Maksimalkan 3x + 4y sesuai dengan batasan berikut:
x + 2y≤ 143x - y≥ 0x - y≤ 2
Fungsi objektif, 3x + 4y, dan batasan diberikan oleh ekspresi linear, yang menjadikannya masalah linear.
Batasan menentukan wilayah yang memungkinkan, yaitu segitiga yang ditampilkan di bawah ini, termasuk bagian dalam.
Langkah-langkah dasar untuk memecahkan masalah LP
Untuk memecahkan masalah LP, program Anda harus menyertakan langkah-langkah berikut:
- Impor wrapper pemecah linear,
- mendeklarasikan pemecah LP,
- mendefinisikan variabel,
- menentukan batasan-batasan,
- menentukan tujuan,
- memanggil pemecah masalah {i>LP<i}; dan
- tampilkan solusi
Solusi menggunakan MPResolver
Bagian berikut menampilkan program yang memecahkan masalah menggunakan wrapper MPSolver dan pemecah LP.
Catatan. Untuk menjalankan program di bawah ini, Anda perlu menginstal OR-Tools.
Pemecah masalah pengoptimalan linear OR-Tools utama adalah Glop, pemecah masalah pemrograman linear internal Google. Cepat, hemat memori, dan stabil secara numerik.
Mengimpor wrapper pemecah masalah linear
Impor (atau sertakan) wrapper pemecah masalah linear OR-Tools, antarmuka untuk pemecah MIP dan pemecah linear, seperti yang ditunjukkan di bawah.
Python
from ortools.linear_solver import pywraplp
C++
#include <iostream> #include <memory> #include "ortools/linear_solver/linear_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable;
C#
using System; using Google.OrTools.LinearSolver;
Mendeklarasikan pemecah LP
MPsolver adalah wrapper untuk beberapa pemecah masalah, termasuk
Glop. Kode di bawah ini mendeklarasikan pemecah GLOP.
Python
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
return
C++
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
LOG(WARNING) << "SCIP solver unavailable.";
return;
}
Java
MPSolver solver = MPSolver.createSolver("GLOP");
C#
Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
return;
}
Catatan: Ganti PDLP dengan GLOP agar dapat menggunakan pemecah masalah LP alternatif. Untuk mengetahui detail
selengkapnya tentang cara memilih pemecah masalah, lihat
pemecahan halaman landing lanjutan, dan untuk penginstalan
pemecah masalah pihak ketiga, lihat panduan penginstalan.
Membuat variabel
Pertama, buat variabel x dan y yang nilainya berada dalam rentang 0 hingga tak terhingga.
Python
x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")
print("Number of variables =", solver.NumVariables())
C++
const double infinity = solver->infinity(); // x and y are non-negative variables. MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Java
double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are continuous non-negative variables.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());
C#
Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables());
Menentukan batasan
Selanjutnya, tentukan batasan pada variabel. Beri nama unik untuk setiap batasan (seperti constraint0), lalu tentukan koefisien untuk
batasan tersebut.
Python
# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)
# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)
# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)
print("Number of constraints =", solver.NumConstraints())
C++
// x + 2*y <= 14. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 2); // 3*x - y >= 0. MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity); c1->SetCoefficient(x, 3); c1->SetCoefficient(y, -1); // x - y <= 2. MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0); c2->SetCoefficient(x, 1); c2->SetCoefficient(y, -1); LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
Java
// x + 2*y <= 14.
MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 2);
// 3*x - y >= 0.
MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
c1.setCoefficient(x, 3);
c1.setCoefficient(y, -1);
// x - y <= 2.
MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
c2.setCoefficient(x, 1);
c2.setCoefficient(y, -1);
System.out.println("Number of constraints = " + solver.numConstraints());
C#
// x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0);
// 3x - y >= 0.
solver.Add(3 * x - y >= 0.0);
// x - y <= 2.
solver.Add(x - y <= 2.0);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());
Menentukan fungsi tujuan
Kode berikut menentukan fungsi objektif, 3x + 4y, dan menentukan bahwa ini adalah masalah maksimalisasi.
Python
# Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y)
C++
// Objective function: 3x + 4y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 3); objective->SetCoefficient(y, 4); objective->SetMaximization();
Java
// Maximize 3 * x + 4 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 3); objective.setCoefficient(y, 4); objective.setMaximization();
C#
// Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y);
Memanggil pemecah masalah
Kode berikut memanggil pemecah.
Python
print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()
C++
const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
LOG(FATAL) << "The problem does not have an optimal solution!";
}
Java
final MPSolver.ResultStatus resultStatus = solver.solve();
C#
Solver.ResultStatus resultStatus = solver.Solve();
Menampilkan solusi
Kode berikut menampilkan solusi.
Python
if status == pywraplp.Solver.OPTIMAL:
print("Solution:")
print(f"Objective value = {solver.Objective().Value():0.1f}")
print(f"x = {x.solution_value():0.1f}")
print(f"y = {y.solution_value():0.1f}")
else:
print("The problem does not have an optimal solution.")
C++
LOG(INFO) << "Solution:"; LOG(INFO) << "Optimal objective value = " << objective->Value(); LOG(INFO) << x->name() << " = " << x->solution_value(); LOG(INFO) << y->name() << " = " << y->solution_value();
Java
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
System.out.println("Solution:");
System.out.println("Objective value = " + objective.value());
System.out.println("x = " + x.solutionValue());
System.out.println("y = " + y.solutionValue());
} else {
System.err.println("The problem does not have an optimal solution!");
}
C#
// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
Console.WriteLine("The problem does not have an optimal solution!");
return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());
Program lengkap
Program lengkapnya ditampilkan di bawah ini.
Python
from ortools.linear_solver import pywraplp
def LinearProgrammingExample():
"""Linear programming sample."""
# Instantiate a Glop solver, naming it LinearExample.
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
return
# Create the two variables and let them take on any non-negative value.
x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")
print("Number of variables =", solver.NumVariables())
# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)
# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)
# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)
print("Number of constraints =", solver.NumConstraints())
# Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y)
# Solve the system.
print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()
if status == pywraplp.Solver.OPTIMAL:
print("Solution:")
print(f"Objective value = {solver.Objective().Value():0.1f}")
print(f"x = {x.solution_value():0.1f}")
print(f"y = {y.solution_value():0.1f}")
else:
print("The problem does not have an optimal solution.")
print("\nAdvanced usage:")
print(f"Problem solved in {solver.wall_time():d} milliseconds")
print(f"Problem solved in {solver.iterations():d} iterations")
LinearProgrammingExample()
C++
#include <iostream>
#include <memory>
#include "ortools/linear_solver/linear_solver.h"
namespace operations_research {
void LinearProgrammingExample() {
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
LOG(WARNING) << "SCIP solver unavailable.";
return;
}
const double infinity = solver->infinity();
// x and y are non-negative variables.
MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
LOG(INFO) << "Number of variables = " << solver->NumVariables();
// x + 2*y <= 14.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0);
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 2);
// 3*x - y >= 0.
MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity);
c1->SetCoefficient(x, 3);
c1->SetCoefficient(y, -1);
// x - y <= 2.
MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0);
c2->SetCoefficient(x, 1);
c2->SetCoefficient(y, -1);
LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
// Objective function: 3x + 4y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 3);
objective->SetCoefficient(y, 4);
objective->SetMaximization();
const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
LOG(FATAL) << "The problem does not have an optimal solution!";
}
LOG(INFO) << "Solution:";
LOG(INFO) << "Optimal objective value = " << objective->Value();
LOG(INFO) << x->name() << " = " << x->solution_value();
LOG(INFO) << y->name() << " = " << y->solution_value();
}
} // namespace operations_research
int main(int argc, char** argv) {
operations_research::LinearProgrammingExample();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;
/** Simple linear programming example. */
public final class LinearProgrammingExample {
public static void main(String[] args) {
Loader.loadNativeLibraries();
MPSolver solver = MPSolver.createSolver("GLOP");
double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are continuous non-negative variables.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());
// x + 2*y <= 14.
MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 2);
// 3*x - y >= 0.
MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
c1.setCoefficient(x, 3);
c1.setCoefficient(y, -1);
// x - y <= 2.
MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
c2.setCoefficient(x, 1);
c2.setCoefficient(y, -1);
System.out.println("Number of constraints = " + solver.numConstraints());
// Maximize 3 * x + 4 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 3);
objective.setCoefficient(y, 4);
objective.setMaximization();
final MPSolver.ResultStatus resultStatus = solver.solve();
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
System.out.println("Solution:");
System.out.println("Objective value = " + objective.value());
System.out.println("x = " + x.solutionValue());
System.out.println("y = " + y.solutionValue());
} else {
System.err.println("The problem does not have an optimal solution!");
}
System.out.println("\nAdvanced usage:");
System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
System.out.println("Problem solved in " + solver.iterations() + " iterations");
}
private LinearProgrammingExample() {}
}
C#
using System;
using Google.OrTools.LinearSolver;
public class LinearProgrammingExample
{
static void Main()
{
Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
return;
}
// x and y are continuous non-negative variables.
Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables());
// x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0);
// 3x - y >= 0.
solver.Add(3 * x - y >= 0.0);
// x - y <= 2.
solver.Add(x - y <= 2.0);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());
// Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y);
Solver.ResultStatus resultStatus = solver.Solve();
// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
Console.WriteLine("The problem does not have an optimal solution!");
return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());
Console.WriteLine("\nAdvanced usage:");
Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
}
}
Solusi yang optimal
Program memberikan solusi optimal untuk masalah tersebut, seperti yang ditunjukkan di bawah.
Number of variables = 2
Number of constraints = 3
Solution:
x = 6.0
y = 4.0
Optimal objective value = 34.0
Berikut adalah grafik yang menunjukkan solusinya:
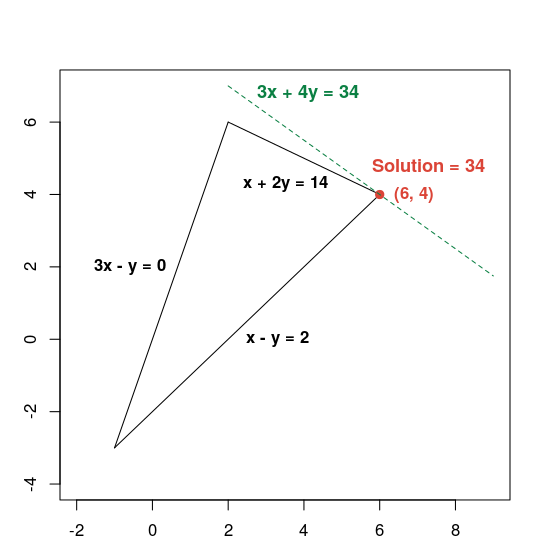
Garis hijau putus-putus ditentukan dengan menetapkan fungsi objektif yang sama dengan nilai optimalnya, yaitu 34. Setiap garis yang persamaannya memiliki bentuk 3x + 4y = c sejajar dengan garis putus-putus, dan 34 adalah nilai terbesar c yang garisnya berpotongan dengan area yang valid.
Untuk mempelajari lebih lanjut cara memecahkan masalah pengoptimalan linear, lihat pemecahan LP lanjutan.
