หน้านี้ได้รับการแปลโดย Cloud Translation API

การแก้ปัญหาเกี่ยวกับ LP

ส่วนต่อไปนี้แสดงตัวอย่างปัญหา LP และแสดงวิธีแก้โจทย์ ปัญหามีดังนี้

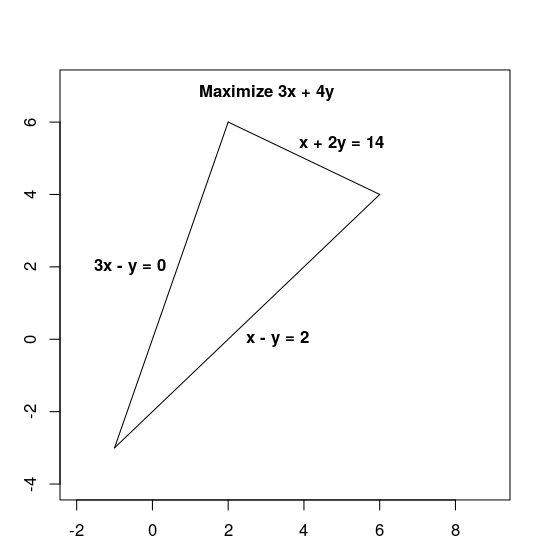
เพิ่ม 3x + 4y ให้มากที่สุดภายใต้ข้อจำกัดต่อไปนี้

x + 2y ≤ 14
3x - y ≥ 0
x - y ≤ 2

ทั้งฟังก์ชันวัตถุประสงค์ 3x + 4y และข้อจํากัดจะกำหนดด้วยนิพจน์เชิงเส้น ซึ่งทำให้เป็นปัญหาเชิงเส้น

ข้อจำกัดจะกำหนดภูมิภาคที่เป็นไปได้ ซึ่งก็คือสามเหลี่ยมที่แสดงด้านล่าง รวมถึงพื้นที่ภายในด้วย

ขั้นตอนพื้นฐานสำหรับการแก้ปัญหาหน้า Landing Page

หากต้องการแก้ปัญหา LP โปรแกรมของคุณควรมีขั้นตอนต่อไปนี้

นำเข้า Wrapper ของตัวแก้วิดีโอเชิงเส้น
ประกาศโปรแกรมแก้ LP
กำหนดตัวแปร
กำหนดข้อจำกัด
กำหนดวัตถุประสงค์
เรียกใช้โปรแกรมแก้ LP และ
แสดงโซลูชัน

โซลูชันที่ใช้ MPSolver

ส่วนต่อไปนี้จะแสดงโปรแกรมที่แก้ปัญหาโดยใช้ Wrapper ของ MPSolver และโปรแกรมแก้โจทย์ LP

หมายเหตุ คุณต้องติดตั้ง OR-Tools เพื่อเรียกใช้โปรแกรมด้านล่าง

เครื่องมือแก้โจทย์การเพิ่มประสิทธิภาพเชิงเส้น "หรือ" เครื่องมือหลักคือ Glop ซึ่งเป็นโปรแกรมแก้ปัญหาโปรแกรมเชิงเส้นภายในของ Google ซึ่งทำงานเร็ว ประหยัดหน่วยความจำ และเสถียรตัวเลข

นำเข้า Wrapper เครื่องมือแก้โจทย์เชิงเส้น

นำเข้า (หรือรวม) Wrapper เครื่องมือแก้โจทย์เชิงเส้น "หรือ" ซึ่งเป็นอินเทอร์เฟซสำหรับเครื่องมือแก้ปัญหา MIP และเครื่องมือแก้โจทย์เชิงเส้นดังที่แสดงด้านล่าง

Python

from ortools.linear_solver import pywraplp

C++

#include <iostream>
#include <memory>

#include "ortools/linear_solver/linear_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

C#

using System;
using Google.OrTools.LinearSolver;

ประกาศเครื่องมือแก้โจทย์ LP

MPsolver คือ Wrapper สำหรับเครื่องมือแก้โจทย์ที่หลากหลาย รวมถึง Glop โค้ดด้านล่างนี้ประกาศเครื่องมือแก้โจทย์ GLOP

Python

solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
    return

C++

std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
  LOG(WARNING) << "SCIP solver unavailable.";
  return;
}

Java

MPSolver solver = MPSolver.createSolver("GLOP");

C#

Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
    return;
}

หมายเหตุ: แทนที่ PDLP ด้วย GLOP เพื่อใช้เครื่องมือแก้ LP อื่น โปรดดูรายละเอียดเพิ่มเติมเกี่ยวกับการเลือกเครื่องมือแก้โจทย์คณิตที่การแก้ LP ขั้นสูง และสำหรับการติดตั้งเครื่องมือแก้โจทย์คณิตของบุคคลที่สาม โปรดดูคู่มือการติดตั้ง

สร้างตัวแปร

ก่อนอื่น ให้สร้างตัวแปร x และ y ซึ่งค่าอยู่ในช่วงตั้งแต่ 0 ถึงค่าอนันต์

Python

x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")

print("Number of variables =", solver.NumVariables())

C++

const double infinity = solver->infinity();
// x and y are non-negative variables.
MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
LOG(INFO) << "Number of variables = " << solver->NumVariables();

Java

double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are continuous non-negative variables.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());

C#

Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());

กําหนดข้อจํากัด

ต่อไป ให้กำหนดข้อจำกัดของตัวแปร ตั้งชื่อที่ไม่ซ้ำกันให้แต่ละจุด (เช่น constraint0) จากนั้นกำหนดค่าสัมประสิทธิ์สำหรับข้อจำกัด

Python

# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)

# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)

# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)

print("Number of constraints =", solver.NumConstraints())

C++

// x + 2*y <= 14.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0);
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 2);

// 3*x - y >= 0.
MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity);
c1->SetCoefficient(x, 3);
c1->SetCoefficient(y, -1);

// x - y <= 2.
MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0);
c2->SetCoefficient(x, 1);
c2->SetCoefficient(y, -1);
LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

Java

// x + 2*y <= 14.
MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 2);

// 3*x - y >= 0.
MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
c1.setCoefficient(x, 3);
c1.setCoefficient(y, -1);

// x - y <= 2.
MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
c2.setCoefficient(x, 1);
c2.setCoefficient(y, -1);
System.out.println("Number of constraints = " + solver.numConstraints());

C#

// x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0);

// 3x - y >= 0.
solver.Add(3 * x - y >= 0.0);

// x - y <= 2.
solver.Add(x - y <= 2.0);

Console.WriteLine("Number of constraints = " + solver.NumConstraints());

กำหนดฟังก์ชันวัตถุประสงค์

โค้ดต่อไปนี้กำหนดฟังก์ชันวัตถุประสงค์ 3x + 4y และระบุว่านี่คือปัญหาการเพิ่มสูงสุด

Python

# Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y)

C++

// Objective function: 3x + 4y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 3);
objective->SetCoefficient(y, 4);
objective->SetMaximization();

Java

// Maximize 3 * x + 4 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 3);
objective.setCoefficient(y, 4);
objective.setMaximization();

C#

// Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y);

เรียกใช้เครื่องมือแก้โจทย์

โค้ดต่อไปนี้จะเรียกเครื่องมือแก้โจทย์

Python

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

C++

const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
  LOG(FATAL) << "The problem does not have an optimal solution!";
}

Java

final MPSolver.ResultStatus resultStatus = solver.solve();

C#

Solver.ResultStatus resultStatus = solver.Solve();

แสดงคำตอบ

โค้ดต่อไปนี้จะแสดงโซลูชัน

Python

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print(f"Objective value = {solver.Objective().Value():0.1f}")
    print(f"x = {x.solution_value():0.1f}")
    print(f"y = {y.solution_value():0.1f}")
else:
    print("The problem does not have an optimal solution.")

C++

LOG(INFO) << "Solution:";
LOG(INFO) << "Optimal objective value = " << objective->Value();
LOG(INFO) << x->name() << " = " << x->solution_value();
LOG(INFO) << y->name() << " = " << y->solution_value();

Java

if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
  System.out.println("Solution:");
  System.out.println("Objective value = " + objective.value());
  System.out.println("x = " + x.solutionValue());
  System.out.println("y = " + y.solutionValue());
} else {
  System.err.println("The problem does not have an optimal solution!");
}

C#

// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
    Console.WriteLine("The problem does not have an optimal solution!");
    return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());

โปรแกรมทั้งหมด

โปรดดูรายการโปรแกรมทั้งหมดด้านล่าง

Python

from ortools.linear_solver import pywraplp


def LinearProgrammingExample():
    """Linear programming sample."""
    # Instantiate a Glop solver, naming it LinearExample.
    solver = pywraplp.Solver.CreateSolver("GLOP")
    if not solver:
        return

    # Create the two variables and let them take on any non-negative value.
    x = solver.NumVar(0, solver.infinity(), "x")
    y = solver.NumVar(0, solver.infinity(), "y")

    print("Number of variables =", solver.NumVariables())

    # Constraint 0: x + 2y <= 14.
    solver.Add(x + 2 * y <= 14.0)

    # Constraint 1: 3x - y >= 0.
    solver.Add(3 * x - y >= 0.0)

    # Constraint 2: x - y <= 2.
    solver.Add(x - y <= 2.0)

    print("Number of constraints =", solver.NumConstraints())

    # Objective function: 3x + 4y.
    solver.Maximize(3 * x + 4 * y)

    # Solve the system.
    print(f"Solving with {solver.SolverVersion()}")
    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Solution:")
        print(f"Objective value = {solver.Objective().Value():0.1f}")
        print(f"x = {x.solution_value():0.1f}")
        print(f"y = {y.solution_value():0.1f}")
    else:
        print("The problem does not have an optimal solution.")

    print("\nAdvanced usage:")
    print(f"Problem solved in {solver.wall_time():d} milliseconds")
    print(f"Problem solved in {solver.iterations():d} iterations")


LinearProgrammingExample()

C++

#include <iostream>
#include <memory>

#include "ortools/linear_solver/linear_solver.h"

namespace operations_research {
void LinearProgrammingExample() {
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  const double infinity = solver->infinity();
  // x and y are non-negative variables.
  MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  // x + 2*y <= 14.
  MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0);
  c0->SetCoefficient(x, 1);
  c0->SetCoefficient(y, 2);

  // 3*x - y >= 0.
  MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity);
  c1->SetCoefficient(x, 3);
  c1->SetCoefficient(y, -1);

  // x - y <= 2.
  MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0);
  c2->SetCoefficient(x, 1);
  c2->SetCoefficient(y, -1);
  LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

  // Objective function: 3x + 4y.
  MPObjective* const objective = solver->MutableObjective();
  objective->SetCoefficient(x, 3);
  objective->SetCoefficient(y, 4);
  objective->SetMaximization();

  const MPSolver::ResultStatus result_status = solver->Solve();
  // Check that the problem has an optimal solution.
  if (result_status != MPSolver::OPTIMAL) {
    LOG(FATAL) << "The problem does not have an optimal solution!";
  }

  LOG(INFO) << "Solution:";
  LOG(INFO) << "Optimal objective value = " << objective->Value();
  LOG(INFO) << x->name() << " = " << x->solution_value();
  LOG(INFO) << y->name() << " = " << y->solution_value();
}
}  // namespace operations_research

int main(int argc, char** argv) {
  operations_research::LinearProgrammingExample();
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

/** Simple linear programming example. */
public final class LinearProgrammingExample {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    MPSolver solver = MPSolver.createSolver("GLOP");

    double infinity = java.lang.Double.POSITIVE_INFINITY;
    // x and y are continuous non-negative variables.
    MPVariable x = solver.makeNumVar(0.0, infinity, "x");
    MPVariable y = solver.makeNumVar(0.0, infinity, "y");
    System.out.println("Number of variables = " + solver.numVariables());

    // x + 2*y <= 14.
    MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
    c0.setCoefficient(x, 1);
    c0.setCoefficient(y, 2);

    // 3*x - y >= 0.
    MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
    c1.setCoefficient(x, 3);
    c1.setCoefficient(y, -1);

    // x - y <= 2.
    MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
    c2.setCoefficient(x, 1);
    c2.setCoefficient(y, -1);
    System.out.println("Number of constraints = " + solver.numConstraints());

    // Maximize 3 * x + 4 * y.
    MPObjective objective = solver.objective();
    objective.setCoefficient(x, 3);
    objective.setCoefficient(y, 4);
    objective.setMaximization();

    final MPSolver.ResultStatus resultStatus = solver.solve();

    if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
      System.out.println("Solution:");
      System.out.println("Objective value = " + objective.value());
      System.out.println("x = " + x.solutionValue());
      System.out.println("y = " + y.solutionValue());
    } else {
      System.err.println("The problem does not have an optimal solution!");
    }

    System.out.println("\nAdvanced usage:");
    System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
    System.out.println("Problem solved in " + solver.iterations() + " iterations");
  }

  private LinearProgrammingExample() {}
}

C#

using System;
using Google.OrTools.LinearSolver;

public class LinearProgrammingExample
{
    static void Main()
    {
        Solver solver = Solver.CreateSolver("GLOP");
        if (solver is null)
        {
            return;
        }
        // x and y are continuous non-negative variables.
        Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
        Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");

        Console.WriteLine("Number of variables = " + solver.NumVariables());

        // x + 2y <= 14.
        solver.Add(x + 2 * y <= 14.0);

        // 3x - y >= 0.
        solver.Add(3 * x - y >= 0.0);

        // x - y <= 2.
        solver.Add(x - y <= 2.0);

        Console.WriteLine("Number of constraints = " + solver.NumConstraints());

        // Objective function: 3x + 4y.
        solver.Maximize(3 * x + 4 * y);

        Solver.ResultStatus resultStatus = solver.Solve();

        // Check that the problem has an optimal solution.
        if (resultStatus != Solver.ResultStatus.OPTIMAL)
        {
            Console.WriteLine("The problem does not have an optimal solution!");
            return;
        }
        Console.WriteLine("Solution:");
        Console.WriteLine("Objective value = " + solver.Objective().Value());
        Console.WriteLine("x = " + x.SolutionValue());
        Console.WriteLine("y = " + y.SolutionValue());

        Console.WriteLine("\nAdvanced usage:");
        Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
        Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
    }
}

โซลูชันที่ดีที่สุด

โปรแกรมจะแสดงวิธีแก้ปัญหาที่เหมาะสมที่สุดตามที่แสดงด้านล่าง

Number of variables = 2
Number of constraints = 3
Solution:
x = 6.0
y = 4.0
Optimal objective value = 34.0

นี่คือกราฟแสดงเฉลย

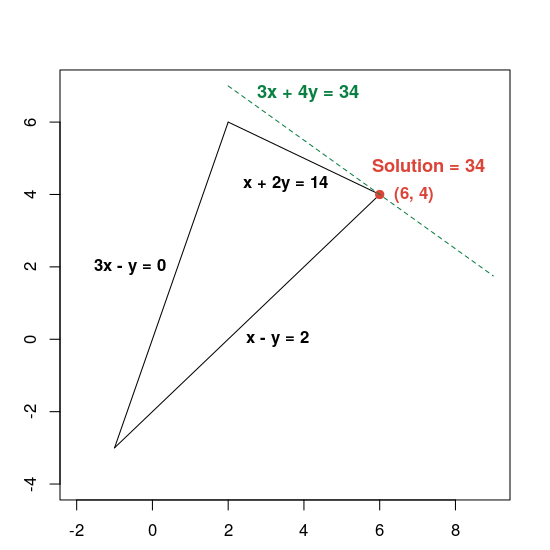
เส้นประสีเขียวจะกำหนดโดยการตั้งค่าฟังก์ชันวัตถุประสงค์ให้เท่ากับค่าที่เหมาะสมที่สุดที่ 34 ทุกบรรทัดที่มีสมการอยู่ในรูปแบบ 3x + 4y = c ขนานกับเส้นประ และ 34 คือค่า c ที่มากที่สุดซึ่งเส้นตัดกับพื้นที่ที่เป็นไปได้

ดูข้อมูลเพิ่มเติมเกี่ยวกับการแก้ปัญหาการเพิ่มประสิทธิภาพเชิงเส้นได้ที่การแก้ปัญหา LP ขั้นสูง