Page Summary
-
This page demonstrates how to solve a linear problem using the OR-Tools MPSolver, focusing on a specific example of maximizing an objective function with given constraints.
-
The solution involves defining variables, constraints, and the objective function within the MPSolver framework before invoking the solver to find the optimal solution.
-
Code examples are provided in Python, C++, Java, and C# to illustrate the implementation of the solution process.
-
The optimal solution for the given example is x = 6.0, y = 4.0, resulting in an objective value of 34.0, which represents the maximum value within the feasible region defined by the constraints.
-
The content also touches upon advanced usage of the MPSolver and directs users to further resources for more in-depth understanding of linear optimization problem-solving.
The following sections present an example of an LP problem and show how to solve it. Here's the problem:
Maximize 3x + 4y subject to the following constraints:
x + 2y≤ 143x - y≥ 0x - y≤ 2
Both the objective function, 3x + 4y, and the constraints are given by linear
expressions, which makes this a linear problem.
The constraints define the feasible region, which is the triangle shown below, including its interior.
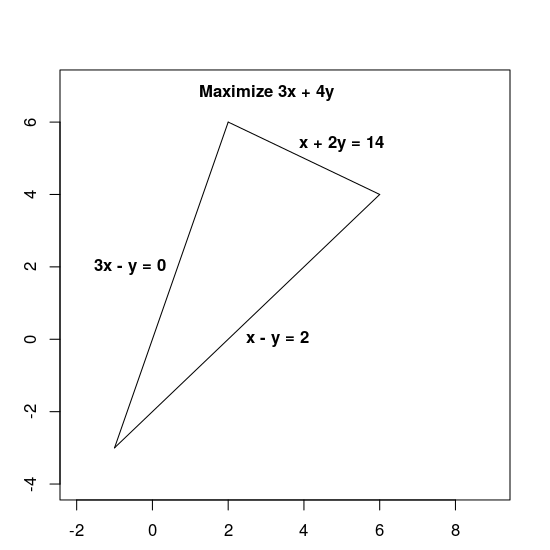
Basic steps for solving an LP problem
To solve a LP problem, your program should include the following steps:
- Import the linear solver wrapper,
- declare the LP solver,
- define the variables,
- define the constraints,
- define the objective,
- call the LP solver; and
- display the solution
Solution using the MPSolver
The following section present a program that solves the problem using the MPSolver wrapper and an LP solver.
Note. To run the program below, you need to install OR-Tools.
The primary OR-Tools linear optimization solver is Glop, Google's in-house linear programming solver. It's fast, memory efficient, and numerically stable.
Import the linear solver wrapper
Import (or include) the OR-Tools linear solver wrapper, an interface for MIP solvers and linear solvers, as shown below.
Python
from ortools.linear_solver import pywraplp
C++
#include <iostream> #include <memory> #include "absl/base/log_severity.h" #include "absl/log/globals.h" #include "ortools/base/init_google.h" #include "ortools/linear_solver/linear_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable;
C#
using System; using Google.OrTools.LinearSolver;
Declare the LP solver
MPsolver is a wrapper for several different solvers, including
Glop. The code below declares the GLOP solver.
Python
solver = pywraplp.Solver.CreateSolver("GLOP") if not solver: return
C++
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP")); if (!solver) { LOG(WARNING) << "SCIP solver unavailable."; return; }
Java
MPSolver solver = MPSolver.createSolver("GLOP");
C#
Solver solver = Solver.CreateSolver("GLOP"); if (solver is null) { return; }
Note: Substitute PDLP for GLOP to use an alternative LP solver. For more
details on choosing solvers, see
advanced LP solving, and for installation of
third-party solvers, see the installation guide.
Create the variables
First, create variables x and y whose values are in the range from 0 to infinity.
Python
x = solver.NumVar(0, solver.infinity(), "x") y = solver.NumVar(0, solver.infinity(), "y") print("Number of variables =", solver.NumVariables())
C++
const double infinity = solver->infinity(); // x and y are non-negative variables. MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Java
double infinity = java.lang.Double.POSITIVE_INFINITY; // x and y are continuous non-negative variables. MPVariable x = solver.makeNumVar(0.0, infinity, "x"); MPVariable y = solver.makeNumVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables());
C#
Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables());
Define the constraints
Next, define the constraints on the variables. Give each constraint a unique
name (such as constraint0), and then define the coefficients for
the constraint.
Python
# Constraint 0: x + 2y <= 14. solver.Add(x + 2 * y <= 14.0) # Constraint 1: 3x - y >= 0. solver.Add(3 * x - y >= 0.0) # Constraint 2: x - y <= 2. solver.Add(x - y <= 2.0) print("Number of constraints =", solver.NumConstraints())
C++
// x + 2*y <= 14. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 2); // 3*x - y >= 0. MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity); c1->SetCoefficient(x, 3); c1->SetCoefficient(y, -1); // x - y <= 2. MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0); c2->SetCoefficient(x, 1); c2->SetCoefficient(y, -1); LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
Java
// x + 2*y <= 14. MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0"); c0.setCoefficient(x, 1); c0.setCoefficient(y, 2); // 3*x - y >= 0. MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1"); c1.setCoefficient(x, 3); c1.setCoefficient(y, -1); // x - y <= 2. MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2"); c2.setCoefficient(x, 1); c2.setCoefficient(y, -1); System.out.println("Number of constraints = " + solver.numConstraints());
C#
// x + 2y <= 14. solver.Add(x + 2 * y <= 14.0); // 3x - y >= 0. solver.Add(3 * x - y >= 0.0); // x - y <= 2. solver.Add(x - y <= 2.0); Console.WriteLine("Number of constraints = " + solver.NumConstraints());
Define the objective function
The following code defines the objective function, 3x + 4y, and specifies that
this is a maximization problem.
Python
# Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y)
C++
// Objective function: 3x + 4y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 3); objective->SetCoefficient(y, 4); objective->SetMaximization();
Java
// Maximize 3 * x + 4 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 3); objective.setCoefficient(y, 4); objective.setMaximization();
C#
// Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y);
Invoke the solver
The following code invokes the solver.
Python
print(f"Solving with {solver.SolverVersion()}") status = solver.Solve()
C++
const MPSolver::ResultStatus result_status = solver->Solve(); // Check that the problem has an optimal solution. if (result_status != MPSolver::OPTIMAL) { LOG(FATAL) << "The problem does not have an optimal solution!"; }
Java
final MPSolver.ResultStatus resultStatus = solver.solve();
C#
Solver.ResultStatus resultStatus = solver.Solve();
Display the solution
The following code displays the solution.
Python
if status == pywraplp.Solver.OPTIMAL: print("Solution:") print(f"Objective value = {solver.Objective().Value():0.1f}") print(f"x = {x.solution_value():0.1f}") print(f"y = {y.solution_value():0.1f}") else: print("The problem does not have an optimal solution.")
C++
LOG(INFO) << "Solution:"; LOG(INFO) << "Optimal objective value = " << objective->Value(); LOG(INFO) << x->name() << " = " << x->solution_value(); LOG(INFO) << y->name() << " = " << y->solution_value();
Java
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) { System.out.println("Solution:"); System.out.println("Objective value = " + objective.value()); System.out.println("x = " + x.solutionValue()); System.out.println("y = " + y.solutionValue()); } else { System.err.println("The problem does not have an optimal solution!"); }
C#
// Check that the problem has an optimal solution. if (resultStatus != Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Solution:"); Console.WriteLine("Objective value = " + solver.Objective().Value()); Console.WriteLine("x = " + x.SolutionValue()); Console.WriteLine("y = " + y.SolutionValue());
The complete programs
The complete programs are shown below.
Python
from ortools.linear_solver import pywraplp def LinearProgrammingExample(): """Linear programming sample.""" # Instantiate a Glop solver, naming it LinearExample. solver = pywraplp.Solver.CreateSolver("GLOP") if not solver: return # Create the two variables and let them take on any non-negative value. x = solver.NumVar(0, solver.infinity(), "x") y = solver.NumVar(0, solver.infinity(), "y") print("Number of variables =", solver.NumVariables()) # Constraint 0: x + 2y <= 14. solver.Add(x + 2 * y <= 14.0) # Constraint 1: 3x - y >= 0. solver.Add(3 * x - y >= 0.0) # Constraint 2: x - y <= 2. solver.Add(x - y <= 2.0) print("Number of constraints =", solver.NumConstraints()) # Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y) # Solve the system. print(f"Solving with {solver.SolverVersion()}") status = solver.Solve() if status == pywraplp.Solver.OPTIMAL: print("Solution:") print(f"Objective value = {solver.Objective().Value():0.1f}") print(f"x = {x.solution_value():0.1f}") print(f"y = {y.solution_value():0.1f}") else: print("The problem does not have an optimal solution.") print("\nAdvanced usage:") print(f"Problem solved in {solver.wall_time():d} milliseconds") print(f"Problem solved in {solver.iterations():d} iterations") LinearProgrammingExample()
C++
#include <iostream> #include <memory> #include "absl/base/log_severity.h" #include "absl/log/globals.h" #include "ortools/base/init_google.h" #include "ortools/linear_solver/linear_solver.h" namespace operations_research { void LinearProgrammingExample() { std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP")); if (!solver) { LOG(WARNING) << "SCIP solver unavailable."; return; } const double infinity = solver->infinity(); // x and y are non-negative variables. MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables(); // x + 2*y <= 14. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 2); // 3*x - y >= 0. MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity); c1->SetCoefficient(x, 3); c1->SetCoefficient(y, -1); // x - y <= 2. MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0); c2->SetCoefficient(x, 1); c2->SetCoefficient(y, -1); LOG(INFO) << "Number of constraints = " << solver->NumConstraints(); // Objective function: 3x + 4y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 3); objective->SetCoefficient(y, 4); objective->SetMaximization(); const MPSolver::ResultStatus result_status = solver->Solve(); // Check that the problem has an optimal solution. if (result_status != MPSolver::OPTIMAL) { LOG(FATAL) << "The problem does not have an optimal solution!"; } LOG(INFO) << "Solution:"; LOG(INFO) << "Optimal objective value = " << objective->Value(); LOG(INFO) << x->name() << " = " << x->solution_value(); LOG(INFO) << y->name() << " = " << y->solution_value(); } } // namespace operations_research int main(int argc, char* argv[]) { InitGoogle(argv[0], &argc, &argv, true); absl::SetStderrThreshold(absl::LogSeverityAtLeast::kInfo); operations_research::LinearProgrammingExample(); return EXIT_SUCCESS; }
Java
package com.google.ortools.linearsolver.samples; import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable; /** Simple linear programming example. */ public final class LinearProgrammingExample { public static void main(String[] args) { Loader.loadNativeLibraries(); MPSolver solver = MPSolver.createSolver("GLOP"); double infinity = java.lang.Double.POSITIVE_INFINITY; // x and y are continuous non-negative variables. MPVariable x = solver.makeNumVar(0.0, infinity, "x"); MPVariable y = solver.makeNumVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables()); // x + 2*y <= 14. MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0"); c0.setCoefficient(x, 1); c0.setCoefficient(y, 2); // 3*x - y >= 0. MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1"); c1.setCoefficient(x, 3); c1.setCoefficient(y, -1); // x - y <= 2. MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2"); c2.setCoefficient(x, 1); c2.setCoefficient(y, -1); System.out.println("Number of constraints = " + solver.numConstraints()); // Maximize 3 * x + 4 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 3); objective.setCoefficient(y, 4); objective.setMaximization(); final MPSolver.ResultStatus resultStatus = solver.solve(); if (resultStatus == MPSolver.ResultStatus.OPTIMAL) { System.out.println("Solution:"); System.out.println("Objective value = " + objective.value()); System.out.println("x = " + x.solutionValue()); System.out.println("y = " + y.solutionValue()); } else { System.err.println("The problem does not have an optimal solution!"); } System.out.println("\nAdvanced usage:"); System.out.println("Problem solved in " + solver.wallTime() + " milliseconds"); System.out.println("Problem solved in " + solver.iterations() + " iterations"); } private LinearProgrammingExample() {} }
C#
using System; using Google.OrTools.LinearSolver; public class LinearProgrammingExample { static void Main() { Solver solver = Solver.CreateSolver("GLOP"); if (solver is null) { return; } // x and y are continuous non-negative variables. Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables()); // x + 2y <= 14. solver.Add(x + 2 * y <= 14.0); // 3x - y >= 0. solver.Add(3 * x - y >= 0.0); // x - y <= 2. solver.Add(x - y <= 2.0); Console.WriteLine("Number of constraints = " + solver.NumConstraints()); // Objective function: 3x + 4y. solver.Maximize(3 * x + 4 * y); Solver.ResultStatus resultStatus = solver.Solve(); // Check that the problem has an optimal solution. if (resultStatus != Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Solution:"); Console.WriteLine("Objective value = " + solver.Objective().Value()); Console.WriteLine("x = " + x.SolutionValue()); Console.WriteLine("y = " + y.SolutionValue()); Console.WriteLine("\nAdvanced usage:"); Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds"); Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations"); } }
Optimal solution
The program returns the optimal solution to the problem, as shown below.
Number of variables = 2
Number of constraints = 3
Solution:
x = 6.0
y = 4.0
Optimal objective value = 34.0
Here is a graph showing the solution:
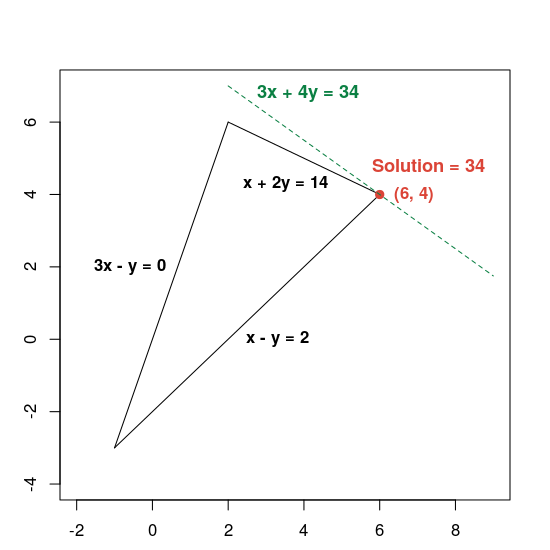
The dashed green line is defined by setting the objective function equal to its
optimal value of 34. Any line whose equation has the form 3x + 4y = c is
parallel to the dashed line, and 34 is the largest value of c for which the line
intersects the feasible region.
To learn more about solving linear optimization problems, see advanced LP solving.
