একটি MIP সমস্যা সমাধান করা

নিম্নলিখিত বিভাগগুলি একটি MIP সমস্যার একটি উদাহরণ উপস্থাপন করে এবং কীভাবে এটি সমাধান করা যায় তা দেখায়। এখানে সমস্যা:

নিম্নলিখিত সীমাবদ্ধতা সাপেক্ষে x + 10y সর্বাধিক করুন:

  1. x + 7y ≤ 17.5
  2. 0 ≤ x ≤ 3.5
  3. 0 ≤ y
  4. x , y পূর্ণসংখ্যা

যেহেতু সীমাবদ্ধতাগুলি রৈখিক, এটি শুধুমাত্র একটি রৈখিক অপ্টিমাইজেশান সমস্যা যেখানে সমাধানগুলিকে পূর্ণসংখ্যা হতে হবে। নীচের গ্রাফটি সমস্যার জন্য সম্ভাব্য অঞ্চলের পূর্ণসংখ্যা বিন্দুগুলি দেখায়।

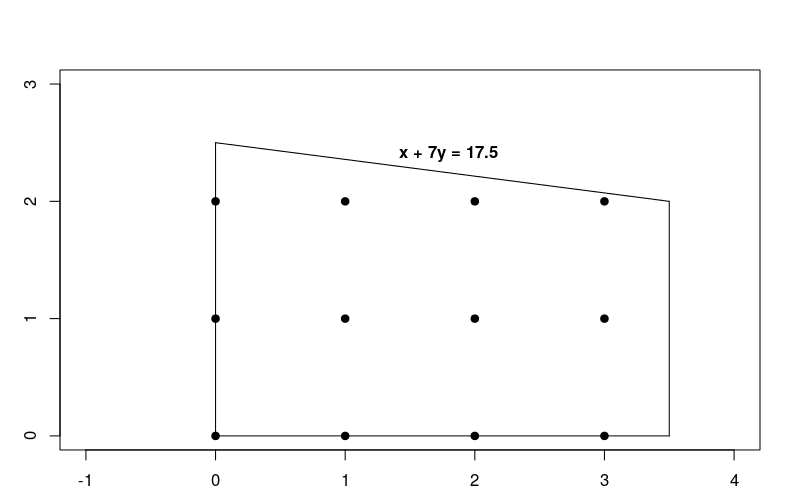
সম্ভাব্য অঞ্চল

লক্ষ্য করুন যে এই সমস্যাটি একটি LP সমস্যা সমাধানে বর্ণিত রৈখিক অপ্টিমাইজেশান সমস্যার সাথে খুব মিল, কিন্তু এই ক্ষেত্রে আমাদের সমাধানগুলিকে পূর্ণসংখ্যা হতে হবে।

একটি MIP সমস্যা সমাধানের জন্য প্রাথমিক পদক্ষেপ

একটি MIP সমস্যা সমাধানের জন্য, আপনার প্রোগ্রামে নিম্নলিখিত পদক্ষেপগুলি অন্তর্ভুক্ত করা উচিত:

  1. রৈখিক সমাধানকারী মোড়ক আমদানি করুন,
  2. এমআইপি সমাধানকারী ঘোষণা করুন,
  3. ভেরিয়েবলের সংজ্ঞা দাও,
  4. সীমাবদ্ধতা সংজ্ঞায়িত করুন,
  5. উদ্দেশ্য সংজ্ঞায়িত করুন,
  6. এমআইপি সমাধানকারীকে কল করুন এবং
  7. সমাধান প্রদর্শন

MPSolver ব্যবহার করে সমাধান

নিম্নলিখিত বিভাগটি একটি প্রোগ্রাম উপস্থাপন করে যা MPSolver র‍্যাপার এবং একটি MIP সল্ভার ব্যবহার করে সমস্যার সমাধান করে।

ডিফল্ট OR-Tools MIP সমাধানকারী হল SCIP ।

রৈখিক সমাধানকারী মোড়ক আমদানি করুন

OR-Tools লিনিয়ার সলভার র্যাপার আমদানি করুন (বা অন্তর্ভুক্ত করুন), এমআইপি সলভার এবং লিনিয়ার সলভারগুলির জন্য একটি ইন্টারফেস, নীচে দেখানো হয়েছে৷

পাইথন

from ortools.linear_solver import pywraplp

সি++

#include <memory>

#include "ortools/linear_solver/linear_solver.h"

জাভা

import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

সি#

using System;
using Google.OrTools.LinearSolver;

এমআইপি সমাধানকারী ঘোষণা করুন

নিম্নলিখিত কোডটি সমস্যার জন্য MIP সমাধানকারী ঘোষণা করে। এই উদাহরণটি তৃতীয়-পক্ষ সমাধানকারী SCIP ব্যবহার করে।

পাইথন

# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SAT")
if not solver:
    return

সি++

// Create the mip solver with the SCIP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
  LOG(WARNING) << "SCIP solver unavailable.";
  return;
}

জাভা

// Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
  System.out.println("Could not create solver SCIP");
  return;
}

সি#

// Create the linear solver with the SCIP backend.
Solver solver = Solver.CreateSolver("SCIP");
if (solver is null)
{
    return;
}

ভেরিয়েবলের সংজ্ঞা দাও

নিম্নলিখিত কোড সমস্যাটির ভেরিয়েবলকে সংজ্ঞায়িত করে।

পাইথন

infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")

print("Number of variables =", solver.NumVariables())

সি++

const double infinity = solver->infinity();
// x and y are integer non-negative variables.
MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

LOG(INFO) << "Number of variables = " << solver->NumVariables();

জাভা

double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are integer non-negative variables.
MPVariable x = solver.makeIntVar(0.0, infinity, "x");
MPVariable y = solver.makeIntVar(0.0, infinity, "y");

System.out.println("Number of variables = " + solver.numVariables());

সি#

// x and y are integer non-negative variables.
Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());

প্রোগ্রামটি ব্যবহার করে MakeIntVar পদ্ধতি (অথবা একটি বৈকল্পিক, কোডিং ভাষার উপর নির্ভর করে) x এবং y ভেরিয়েবল তৈরি করতে যা নেতিবাচক পূর্ণসংখ্যার মান গ্রহণ করে না।

সীমাবদ্ধতা সংজ্ঞায়িত করুন

নিম্নলিখিত কোড সমস্যার জন্য সীমাবদ্ধতা সংজ্ঞায়িত করে।

পাইথন

# x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5)

# x <= 3.5.
solver.Add(x <= 3.5)

print("Number of constraints =", solver.NumConstraints())

সি++

// x + 7 * y <= 17.5.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 7);

// x <= 3.5.
MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
c1->SetCoefficient(x, 1);
c1->SetCoefficient(y, 0);

LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

জাভা

// x + 7 * y <= 17.5.
MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 7);

// x <= 3.5.
MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
c1.setCoefficient(x, 1);
c1.setCoefficient(y, 0);

System.out.println("Number of constraints = " + solver.numConstraints());

সি#

// x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5);

// x <= 3.5.
solver.Add(x <= 3.5);

Console.WriteLine("Number of constraints = " + solver.NumConstraints());

উদ্দেশ্য সংজ্ঞায়িত করুন

নিম্নলিখিত কোড সমস্যার জন্য objective function সংজ্ঞায়িত করে।

পাইথন

# Maximize x + 10 * y.
solver.Maximize(x + 10 * y)

সি++

// Maximize x + 10 * y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 1);
objective->SetCoefficient(y, 10);
objective->SetMaximization();

জাভা

// Maximize x + 10 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 1);
objective.setCoefficient(y, 10);
objective.setMaximization();

সি#

// Maximize x + 10 * y.
solver.Maximize(x + 10 * y);

সমাধানকারীকে কল করুন

নিম্নলিখিত কোড সমাধানকারী কল.

পাইথন

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

সি++

const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
  LOG(FATAL) << "The problem does not have an optimal solution!";
}

জাভা

final MPSolver.ResultStatus resultStatus = solver.solve();

সি#

Solver.ResultStatus resultStatus = solver.Solve();

সমাধান প্রদর্শন করুন

নিম্নলিখিত কোড সমাধান প্রদর্শন করে.

পাইথন

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print("Objective value =", solver.Objective().Value())
    print("x =", x.solution_value())
    print("y =", y.solution_value())
else:
    print("The problem does not have an optimal solution.")

সি++

LOG(INFO) << "Solution:";
LOG(INFO) << "Objective value = " << objective->Value();
LOG(INFO) << "x = " << x->solution_value();
LOG(INFO) << "y = " << y->solution_value();

জাভা

if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
  System.out.println("Solution:");
  System.out.println("Objective value = " + objective.value());
  System.out.println("x = " + x.solutionValue());
  System.out.println("y = " + y.solutionValue());
} else {
  System.err.println("The problem does not have an optimal solution!");
}

সি#

// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
    Console.WriteLine("The problem does not have an optimal solution!");
    return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());

এখানে সমস্যার সমাধান।

Number of variables = 2
Number of constraints = 2
Solution:
Objective value = 23
x = 3
y = 2

উদ্দেশ্য ফাংশনের সর্বোত্তম মান হল 23, যা x = 3 , y = 2 বিন্দুতে ঘটে।

সম্পূর্ণ প্রোগ্রাম

এখানে সম্পূর্ণ প্রোগ্রাম আছে.

পাইথন

from ortools.linear_solver import pywraplp


def main():
    # Create the mip solver with the SCIP backend.
    solver = pywraplp.Solver.CreateSolver("SAT")
    if not solver:
        return

    infinity = solver.infinity()
    # x and y are integer non-negative variables.
    x = solver.IntVar(0.0, infinity, "x")
    y = solver.IntVar(0.0, infinity, "y")

    print("Number of variables =", solver.NumVariables())

    # x + 7 * y <= 17.5.
    solver.Add(x + 7 * y <= 17.5)

    # x <= 3.5.
    solver.Add(x <= 3.5)

    print("Number of constraints =", solver.NumConstraints())

    # Maximize x + 10 * y.
    solver.Maximize(x + 10 * y)

    print(f"Solving with {solver.SolverVersion()}")
    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Solution:")
        print("Objective value =", solver.Objective().Value())
        print("x =", x.solution_value())
        print("y =", y.solution_value())
    else:
        print("The problem does not have an optimal solution.")

    print("\nAdvanced usage:")
    print(f"Problem solved in {solver.wall_time():d} milliseconds")
    print(f"Problem solved in {solver.iterations():d} iterations")
    print(f"Problem solved in {solver.nodes():d} branch-and-bound nodes")


if __name__ == "__main__":
    main()

সি++

#include <memory>

#include "ortools/linear_solver/linear_solver.h"

namespace operations_research {
void SimpleMipProgram() {
  // Create the mip solver with the SCIP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  const double infinity = solver->infinity();
  // x and y are integer non-negative variables.
  MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  // x + 7 * y <= 17.5.
  MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
  c0->SetCoefficient(x, 1);
  c0->SetCoefficient(y, 7);

  // x <= 3.5.
  MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
  c1->SetCoefficient(x, 1);
  c1->SetCoefficient(y, 0);

  LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

  // Maximize x + 10 * y.
  MPObjective* const objective = solver->MutableObjective();
  objective->SetCoefficient(x, 1);
  objective->SetCoefficient(y, 10);
  objective->SetMaximization();

  const MPSolver::ResultStatus result_status = solver->Solve();
  // Check that the problem has an optimal solution.
  if (result_status != MPSolver::OPTIMAL) {
    LOG(FATAL) << "The problem does not have an optimal solution!";
  }

  LOG(INFO) << "Solution:";
  LOG(INFO) << "Objective value = " << objective->Value();
  LOG(INFO) << "x = " << x->solution_value();
  LOG(INFO) << "y = " << y->solution_value();

  LOG(INFO) << "\nAdvanced usage:";
  LOG(INFO) << "Problem solved in " << solver->wall_time() << " milliseconds";
  LOG(INFO) << "Problem solved in " << solver->iterations() << " iterations";
  LOG(INFO) << "Problem solved in " << solver->nodes()
            << " branch-and-bound nodes";
}
}  // namespace operations_research

int main(int argc, char** argv) {
  operations_research::SimpleMipProgram();
  return EXIT_SUCCESS;
}

জাভা

package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

/** Minimal Mixed Integer Programming example to showcase calling the solver. */
public final class SimpleMipProgram {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Create the linear solver with the SCIP backend.
    MPSolver solver = MPSolver.createSolver("SCIP");
    if (solver == null) {
      System.out.println("Could not create solver SCIP");
      return;
    }

    double infinity = java.lang.Double.POSITIVE_INFINITY;
    // x and y are integer non-negative variables.
    MPVariable x = solver.makeIntVar(0.0, infinity, "x");
    MPVariable y = solver.makeIntVar(0.0, infinity, "y");

    System.out.println("Number of variables = " + solver.numVariables());

    // x + 7 * y <= 17.5.
    MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
    c0.setCoefficient(x, 1);
    c0.setCoefficient(y, 7);

    // x <= 3.5.
    MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
    c1.setCoefficient(x, 1);
    c1.setCoefficient(y, 0);

    System.out.println("Number of constraints = " + solver.numConstraints());

    // Maximize x + 10 * y.
    MPObjective objective = solver.objective();
    objective.setCoefficient(x, 1);
    objective.setCoefficient(y, 10);
    objective.setMaximization();

    final MPSolver.ResultStatus resultStatus = solver.solve();

    if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
      System.out.println("Solution:");
      System.out.println("Objective value = " + objective.value());
      System.out.println("x = " + x.solutionValue());
      System.out.println("y = " + y.solutionValue());
    } else {
      System.err.println("The problem does not have an optimal solution!");
    }

    System.out.println("\nAdvanced usage:");
    System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
    System.out.println("Problem solved in " + solver.iterations() + " iterations");
    System.out.println("Problem solved in " + solver.nodes() + " branch-and-bound nodes");
  }

  private SimpleMipProgram() {}
}

সি#

using System;
using Google.OrTools.LinearSolver;

public class SimpleMipProgram
{
    static void Main()
    {
        // Create the linear solver with the SCIP backend.
        Solver solver = Solver.CreateSolver("SCIP");
        if (solver is null)
        {
            return;
        }

        // x and y are integer non-negative variables.
        Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
        Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

        Console.WriteLine("Number of variables = " + solver.NumVariables());

        // x + 7 * y <= 17.5.
        solver.Add(x + 7 * y <= 17.5);

        // x <= 3.5.
        solver.Add(x <= 3.5);

        Console.WriteLine("Number of constraints = " + solver.NumConstraints());

        // Maximize x + 10 * y.
        solver.Maximize(x + 10 * y);

        Solver.ResultStatus resultStatus = solver.Solve();

        // Check that the problem has an optimal solution.
        if (resultStatus != Solver.ResultStatus.OPTIMAL)
        {
            Console.WriteLine("The problem does not have an optimal solution!");
            return;
        }
        Console.WriteLine("Solution:");
        Console.WriteLine("Objective value = " + solver.Objective().Value());
        Console.WriteLine("x = " + x.SolutionValue());
        Console.WriteLine("y = " + y.SolutionValue());

        Console.WriteLine("\nAdvanced usage:");
        Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
        Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
        Console.WriteLine("Problem solved in " + solver.Nodes() + " branch-and-bound nodes");
    }
}

লিনিয়ার এবং ইন্টিজার অপ্টিমাইজেশান তুলনা করা

আসুন উপরে দেখানো পূর্ণসংখ্যা অপ্টিমাইজেশান সমস্যার সমাধানটিকে সংশ্লিষ্ট রৈখিক অপ্টিমাইজেশান সমস্যার সমাধানের সাথে তুলনা করি, যেখানে পূর্ণসংখ্যার সীমাবদ্ধতাগুলি সরানো হয়। আপনি অনুমান করতে পারেন যে পূর্ণসংখ্যা সমস্যার সমাধানটি রৈখিক সমাধানের নিকটতম সম্ভাব্য অঞ্চলের পূর্ণসংখ্যা বিন্দু হবে — যথা, বিন্দু x = 0 , y = 2 । কিন্তু আপনি পরবর্তীতে দেখতে পাবেন, এটি এমন নয়।

আপনি নিম্নলিখিত পরিবর্তনগুলি করে রৈখিক সমস্যা সমাধানের জন্য পূর্ববর্তী বিভাগে সহজেই প্রোগ্রামটি পরিবর্তন করতে পারেন:

  • MIP সমাধানকারী প্রতিস্থাপন করুন

    পাইথন

    # Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SAT")
if not solver:
    return

    সি++

    // Create the mip solver with the SCIP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
  LOG(WARNING) << "SCIP solver unavailable.";
  return;
}

    জাভা

    // Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
  System.out.println("Could not create solver SCIP");
  return;
}

    সি#

    // Create the linear solver with the SCIP backend.
Solver solver = Solver.CreateSolver("SCIP");
if (solver is null)
{
    return;
}
    এলপি সলভারের সাথে

    পাইথন

    # Create the linear solver with the GLOP backend.
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
    return

    সি++

    // Create the linear solver with the GLOP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("GLOP"));

    জাভা

    // Create the linear solver with the GLOP backend.
MPSolver solver = MPSolver.createSolver("GLOP");
if (solver == null) {
  System.out.println("Could not create solver SCIP");
  return;
}

    সি#

    // Create the linear solver with the GLOP backend.
Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
    return;
}
  • পূর্ণসংখ্যা ভেরিয়েবলগুলি প্রতিস্থাপন করুন

    পাইথন

    infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")

print("Number of variables =", solver.NumVariables())

    সি++

    const double infinity = solver->infinity();
// x and y are integer non-negative variables.
MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

LOG(INFO) << "Number of variables = " << solver->NumVariables();

    জাভা

    double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are integer non-negative variables.
MPVariable x = solver.makeIntVar(0.0, infinity, "x");
MPVariable y = solver.makeIntVar(0.0, infinity, "y");

System.out.println("Number of variables = " + solver.numVariables());

    সি#

    // x and y are integer non-negative variables.
Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());
    ক্রমাগত ভেরিয়েবল সহ

    পাইথন

    infinity = solver.infinity()
# Create the variables x and y.
x = solver.NumVar(0.0, infinity, "x")
y = solver.NumVar(0.0, infinity, "y")

print("Number of variables =", solver.NumVariables())

    সি++

    const double infinity = solver->infinity();
// Create the variables x and y.
MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");

LOG(INFO) << "Number of variables = " << solver->NumVariables();

    জাভা

    double infinity = java.lang.Double.POSITIVE_INFINITY;
// Create the variables x and y.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");

System.out.println("Number of variables = " + solver.numVariables());

    সি#

    // Create the variables x and y.
Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());

এই পরিবর্তনগুলি করার পরে এবং আবার প্রোগ্রাম চালানোর পরে, আপনি নিম্নলিখিত আউটপুট পাবেন:

Number of variables = 2
Number of constraints = 2
Objective value = 25.000000
x = 0.000000
y = 2.500000

রৈখিক সমস্যার সমাধান x = 0 , y = 2.5 বিন্দুতে ঘটে, যেখানে উদ্দেশ্য ফাংশনটি 25 এর সমান। এখানে রৈখিক এবং পূর্ণসংখ্যা উভয় সমস্যার সমাধান দেখানো একটি গ্রাফ রয়েছে।

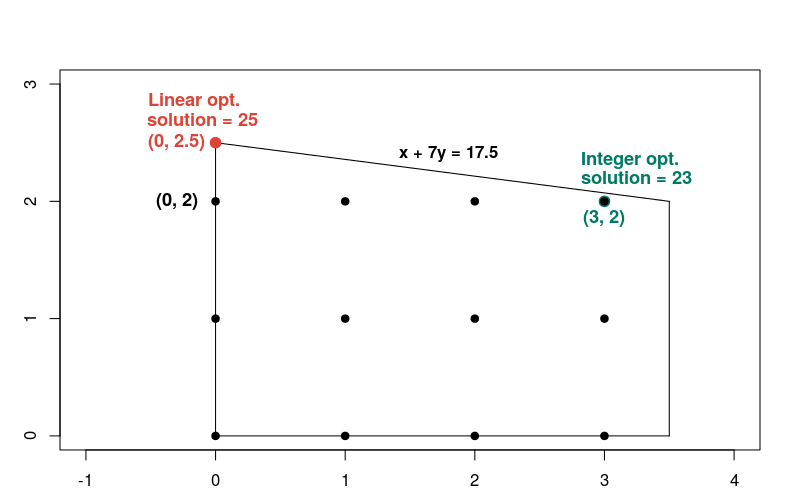
লক্ষ্য করুন যে পূর্ণসংখ্যা সমাধানটি সম্ভাব্য অঞ্চলের বেশিরভাগ অন্যান্য পূর্ণসংখ্যা বিন্দুর তুলনায় রৈখিক সমাধানের কাছাকাছি নয়। সাধারণভাবে, একটি রৈখিক অপ্টিমাইজেশান সমস্যার সমাধান এবং সংশ্লিষ্ট পূর্ণসংখ্যা অপ্টিমাইজেশান সমস্যাগুলি অনেক দূরে হতে পারে। এই কারণে, দুই ধরনের সমস্যা তাদের সমাধানের জন্য বিভিন্ন পদ্ধতির প্রয়োজন।