פתרון בעיות ב-MIP

בקטעים הבאים מוצגת דוגמה לבעיית MIP ומסבירים איך לפתור אותה. הנה הבעיה:

הגדלה מקסימלית של x + 10y בכפוף להגבלות הבאות:

1. x + 7y ≤ 17.5
2. 0 ≤ x ≤ 3.5
3. 0 ≤ y
4. x, y מספרים שלמים

מאחר שהמגבלות הן לינאריות, מדובר רק בבעיית אופטימיזציה לינארית שבה הפתרונות צריכים להיות מספרים שלמים. בתרשים הבא מוצגות נקודות המספרים השלמים באזור שבו הבעיה אפשרית.

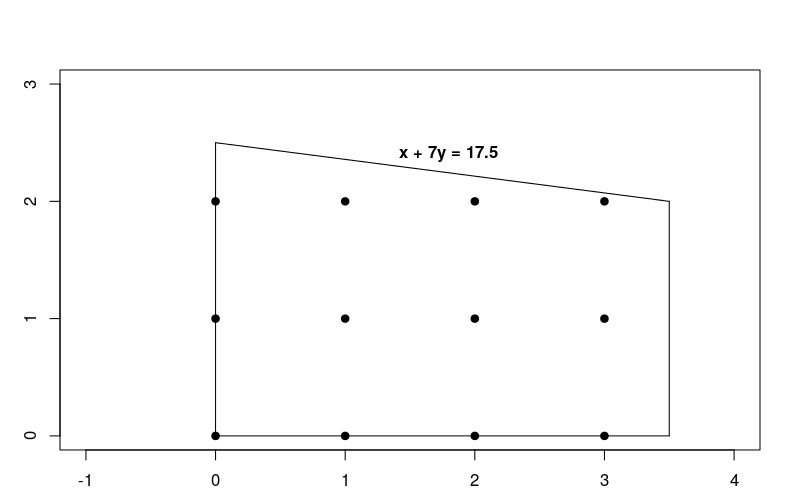
שימו לב שהבעיה הזו דומה מאוד לבעיית האופטימיזציה הלינארית שמתוארת במאמר פתרון בעיות של בעיות LP, אבל במקרה הזה הפתרון צריך להיות מספרים שלמים.

שלבים בסיסיים לפתרון בעיית MIP

כדי לפתור בעיה של MIP, התוכנית צריכה לכלול את השלבים הבאים:

1. מייבאים את ה-wrapper של הפותר הלינארי
2. מצהירים על פותר ה-MIP,
3. להגדיר את המשתנים,
4. להגדיר את האילוצים,
5. להגדיר את היעד,
6. קוראים לפותר MIP
7. הצגת הפתרון

הפתרון באמצעות MPSolver

בקטע הבא מוצגת תוכנה לפתרון הבעיה באמצעות wrapper של MPSolver ופותר MIP.

הערה: כדי להריץ את התוכנה שלמטה, צריך להתקין את OR-Tools.

פותר ברירת המחדל של OR-Tools MIP הוא SCIP.

ייבוא ה-wrapper של הפותר הלינארי

מייבאים (או כוללים) את ה-wrapper של הפתרון הלינארי OR-Tools, ממשק לפותרי MIP ולפותרים ליניאריים, כפי שמתואר בהמשך.

Python

from ortools.linear_solver import pywraplp

C++

#include <memory>

#include "ortools/linear_solver/linear_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

C#

using System;
using Google.OrTools.LinearSolver;

הצהרה על פותר ה-MIP

הקוד הבא מצהיר על פותר ה-MIP של הבעיה. בדוגמה הזו נשתמש בפותר הבעיות של צד שלישי, SCIP.

הערה: אם אתם יוצרים OR-Tools מהמקור ורוצים להתקין ולהשתמש בפתרון אחר, תוכלו להיעזר במדריך ההתקנה של הפלטפורמה שלכם.

Python

# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SAT")
if not solver:
    return

C++

// Create the mip solver with the SCIP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
  LOG(WARNING) << "SCIP solver unavailable.";
  return;
}

Java

// Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
  System.out.println("Could not create solver SCIP");
  return;
}

C#

// Create the linear solver with the SCIP backend.
Solver solver = Solver.CreateSolver("SCIP");
if (solver is null)
{
    return;
}

הגדרת המשתנים

הקוד הבא מגדיר את המשתנים בבעיה.

Python

infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")

print("Number of variables =", solver.NumVariables())

C++

const double infinity = solver->infinity();
// x and y are integer non-negative variables.
MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

LOG(INFO) << "Number of variables = " << solver->NumVariables();

Java

double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are integer non-negative variables.
MPVariable x = solver.makeIntVar(0.0, infinity, "x");
MPVariable y = solver.makeIntVar(0.0, infinity, "y");

System.out.println("Number of variables = " + solver.numVariables());

C#

// x and y are integer non-negative variables.
Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());

בתוכנית משתמשים בשיטה MakeIntVar (או בווריאנט, בהתאם לשפת התכנות) כדי ליצור משתנים x ו-y שמקבלים ערכים של מספרים שלמים לא שליליים.

מגדירים את האילוצים

הקוד הבא מגדיר את המגבלות של הבעיה.

Python

# x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5)

# x <= 3.5.
solver.Add(x <= 3.5)

print("Number of constraints =", solver.NumConstraints())

C++

// x + 7 * y <= 17.5.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 7);

// x <= 3.5.
MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
c1->SetCoefficient(x, 1);
c1->SetCoefficient(y, 0);

LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

Java

// x + 7 * y <= 17.5.
MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 7);

// x <= 3.5.
MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
c1.setCoefficient(x, 1);
c1.setCoefficient(y, 0);

System.out.println("Number of constraints = " + solver.numConstraints());

C#

// x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5);

// x <= 3.5.
solver.Add(x <= 3.5);

Console.WriteLine("Number of constraints = " + solver.NumConstraints());

מגדירים את היעד

הקוד הבא מגדיר את objective function של הבעיה.

Python

# Maximize x + 10 * y.
solver.Maximize(x + 10 * y)

C++

// Maximize x + 10 * y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 1);
objective->SetCoefficient(y, 10);
objective->SetMaximization();

Java

// Maximize x + 10 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 1);
objective.setCoefficient(y, 10);
objective.setMaximization();

C#

// Maximize x + 10 * y.
solver.Maximize(x + 10 * y);

קריאה לפותר

הקוד הבא מפעיל את הפותר.

Python

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

C++

const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
  LOG(FATAL) << "The problem does not have an optimal solution!";
}

Java

final MPSolver.ResultStatus resultStatus = solver.solve();

C#

Solver.ResultStatus resultStatus = solver.Solve();

הצגת הפתרון

הקוד הבא מציג את הפתרון.

Python

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print("Objective value =", solver.Objective().Value())
    print("x =", x.solution_value())
    print("y =", y.solution_value())
else:
    print("The problem does not have an optimal solution.")

C++

LOG(INFO) << "Solution:";
LOG(INFO) << "Objective value = " << objective->Value();
LOG(INFO) << "x = " << x->solution_value();
LOG(INFO) << "y = " << y->solution_value();

Java

if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
  System.out.println("Solution:");
  System.out.println("Objective value = " + objective.value());
  System.out.println("x = " + x.solutionValue());
  System.out.println("y = " + y.solutionValue());
} else {
  System.err.println("The problem does not have an optimal solution!");
}

C#

// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
    Console.WriteLine("The problem does not have an optimal solution!");
    return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());

הנה הפתרון לבעיה.

Number of variables = 2
Number of constraints = 2
Solution:
Objective value = 23
x = 3
y = 2

הערך האופטימלי של פונקציית היעד הוא 23, שמתרחש בנקודה x = 3, y = 2.

השלמה של תוכניות

אלה התוכניות המלאות.

Python

from ortools.linear_solver import pywraplp


def main():
    # Create the mip solver with the SCIP backend.
    solver = pywraplp.Solver.CreateSolver("SAT")
    if not solver:
        return

    infinity = solver.infinity()
    # x and y are integer non-negative variables.
    x = solver.IntVar(0.0, infinity, "x")
    y = solver.IntVar(0.0, infinity, "y")

    print("Number of variables =", solver.NumVariables())

    # x + 7 * y <= 17.5.
    solver.Add(x + 7 * y <= 17.5)

    # x <= 3.5.
    solver.Add(x <= 3.5)

    print("Number of constraints =", solver.NumConstraints())

    # Maximize x + 10 * y.
    solver.Maximize(x + 10 * y)

    print(f"Solving with {solver.SolverVersion()}")
    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Solution:")
        print("Objective value =", solver.Objective().Value())
        print("x =", x.solution_value())
        print("y =", y.solution_value())
    else:
        print("The problem does not have an optimal solution.")

    print("\nAdvanced usage:")
    print(f"Problem solved in {solver.wall_time():d} milliseconds")
    print(f"Problem solved in {solver.iterations():d} iterations")
    print(f"Problem solved in {solver.nodes():d} branch-and-bound nodes")


if __name__ == "__main__":
    main()

C++

#include <memory>

#include "ortools/linear_solver/linear_solver.h"

namespace operations_research {
void SimpleMipProgram() {
  // Create the mip solver with the SCIP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  const double infinity = solver->infinity();
  // x and y are integer non-negative variables.
  MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  // x + 7 * y <= 17.5.
  MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
  c0->SetCoefficient(x, 1);
  c0->SetCoefficient(y, 7);

  // x <= 3.5.
  MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
  c1->SetCoefficient(x, 1);
  c1->SetCoefficient(y, 0);

  LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

  // Maximize x + 10 * y.
  MPObjective* const objective = solver->MutableObjective();
  objective->SetCoefficient(x, 1);
  objective->SetCoefficient(y, 10);
  objective->SetMaximization();

  const MPSolver::ResultStatus result_status = solver->Solve();
  // Check that the problem has an optimal solution.
  if (result_status != MPSolver::OPTIMAL) {
    LOG(FATAL) << "The problem does not have an optimal solution!";
  }

  LOG(INFO) << "Solution:";
  LOG(INFO) << "Objective value = " << objective->Value();
  LOG(INFO) << "x = " << x->solution_value();
  LOG(INFO) << "y = " << y->solution_value();

  LOG(INFO) << "\nAdvanced usage:";
  LOG(INFO) << "Problem solved in " << solver->wall_time() << " milliseconds";
  LOG(INFO) << "Problem solved in " << solver->iterations() << " iterations";
  LOG(INFO) << "Problem solved in " << solver->nodes()
            << " branch-and-bound nodes";
}
}  // namespace operations_research

int main(int argc, char** argv) {
  operations_research::SimpleMipProgram();
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

/** Minimal Mixed Integer Programming example to showcase calling the solver. */
public final class SimpleMipProgram {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Create the linear solver with the SCIP backend.
    MPSolver solver = MPSolver.createSolver("SCIP");
    if (solver == null) {
      System.out.println("Could not create solver SCIP");
      return;
    }

    double infinity = java.lang.Double.POSITIVE_INFINITY;
    // x and y are integer non-negative variables.
    MPVariable x = solver.makeIntVar(0.0, infinity, "x");
    MPVariable y = solver.makeIntVar(0.0, infinity, "y");

    System.out.println("Number of variables = " + solver.numVariables());

    // x + 7 * y <= 17.5.
    MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
    c0.setCoefficient(x, 1);
    c0.setCoefficient(y, 7);

    // x <= 3.5.
    MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
    c1.setCoefficient(x, 1);
    c1.setCoefficient(y, 0);

    System.out.println("Number of constraints = " + solver.numConstraints());

    // Maximize x + 10 * y.
    MPObjective objective = solver.objective();
    objective.setCoefficient(x, 1);
    objective.setCoefficient(y, 10);
    objective.setMaximization();

    final MPSolver.ResultStatus resultStatus = solver.solve();

    if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
      System.out.println("Solution:");
      System.out.println("Objective value = " + objective.value());
      System.out.println("x = " + x.solutionValue());
      System.out.println("y = " + y.solutionValue());
    } else {
      System.err.println("The problem does not have an optimal solution!");
    }

    System.out.println("\nAdvanced usage:");
    System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
    System.out.println("Problem solved in " + solver.iterations() + " iterations");
    System.out.println("Problem solved in " + solver.nodes() + " branch-and-bound nodes");
  }

  private SimpleMipProgram() {}
}

C#

using System;
using Google.OrTools.LinearSolver;

public class SimpleMipProgram
{
    static void Main()
    {
        // Create the linear solver with the SCIP backend.
        Solver solver = Solver.CreateSolver("SCIP");
        if (solver is null)
        {
            return;
        }

        // x and y are integer non-negative variables.
        Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
        Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

        Console.WriteLine("Number of variables = " + solver.NumVariables());

        // x + 7 * y <= 17.5.
        solver.Add(x + 7 * y <= 17.5);

        // x <= 3.5.
        solver.Add(x <= 3.5);

        Console.WriteLine("Number of constraints = " + solver.NumConstraints());

        // Maximize x + 10 * y.
        solver.Maximize(x + 10 * y);

        Solver.ResultStatus resultStatus = solver.Solve();

        // Check that the problem has an optimal solution.
        if (resultStatus != Solver.ResultStatus.OPTIMAL)
        {
            Console.WriteLine("The problem does not have an optimal solution!");
            return;
        }
        Console.WriteLine("Solution:");
        Console.WriteLine("Objective value = " + solver.Objective().Value());
        Console.WriteLine("x = " + x.SolutionValue());
        Console.WriteLine("y = " + y.SolutionValue());

        Console.WriteLine("\nAdvanced usage:");
        Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
        Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
        Console.WriteLine("Problem solved in " + solver.Nodes() + " branch-and-bound nodes");
    }
}

השוואה בין אופטימיזציה ליניארית לבין אופטימיזציה של מספרים שלמים

נשווה את הפתרון לבעיית האופטימיזציה עם מספרים שלמים, המוצגת למעלה, עם הפתרון לבעיית האופטימיזציה הלינארית המתאימה, שבה מסירים את האילוצים של מספרים שלמים. אפשר לנחש שהפתרון לבעיה עם המספר השלם יהיה נקודת המספר השלם באזור האפשרי הקרוב ביותר לפתרון הלינארי, כלומר הנקודה x = 0, y = 2. אבל כפי שתראו בהמשך, זה לא המקרה.

תוכלו לשנות בקלות את התוכנה בקטע הקודם כדי לפתור את הבעיה הלינארית, על ידי ביצוע השינויים הבאים:

• החלפת פותר MIP

  Python

  # Create the mip solver with the SCIP backend.
  solver = pywraplp.Solver.CreateSolver("SAT")
  if not solver:
      return

  C++

  // Create the mip solver with the SCIP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  Java

  // Create the linear solver with the SCIP backend.
  MPSolver solver = MPSolver.createSolver("SCIP");
  if (solver == null) {
    System.out.println("Could not create solver SCIP");
    return;
  }

  C#

  // Create the linear solver with the SCIP backend.
  Solver solver = Solver.CreateSolver("SCIP");
  if (solver is null)
  {
      return;
  }

  בעזרת פותר הבעיות

  Python

  # Create the linear solver with the GLOP backend.
  solver = pywraplp.Solver.CreateSolver("GLOP")
  if not solver:
      return

  C++

  // Create the linear solver with the GLOP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("GLOP"));

  Java

  // Create the linear solver with the GLOP backend.
  MPSolver solver = MPSolver.createSolver("GLOP");
  if (solver == null) {
    System.out.println("Could not create solver SCIP");
    return;
  }

  C#

  // Create the linear solver with the GLOP backend.
  Solver solver = Solver.CreateSolver("GLOP");
  if (solver is null)
  {
      return;
  }

• החלפת משתני המספרים השלמים

  Python

  infinity = solver.infinity()
  # x and y are integer non-negative variables.
  x = solver.IntVar(0.0, infinity, "x")
  y = solver.IntVar(0.0, infinity, "y")
  
  print("Number of variables =", solver.NumVariables())

  C++

  const double infinity = solver->infinity();
  // x and y are integer non-negative variables.
  MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");
  
  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  Java

  double infinity = java.lang.Double.POSITIVE_INFINITY;
  // x and y are integer non-negative variables.
  MPVariable x = solver.makeIntVar(0.0, infinity, "x");
  MPVariable y = solver.makeIntVar(0.0, infinity, "y");
  
  System.out.println("Number of variables = " + solver.numVariables());

  C#

  // x and y are integer non-negative variables.
  Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
  Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");
  
  Console.WriteLine("Number of variables = " + solver.NumVariables());

  עם משתנים רציפים

  Python

  infinity = solver.infinity()
  # Create the variables x and y.
  x = solver.NumVar(0.0, infinity, "x")
  y = solver.NumVar(0.0, infinity, "y")
  
  print("Number of variables =", solver.NumVariables())

  C++

  const double infinity = solver->infinity();
  // Create the variables x and y.
  MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
  
  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  Java

  double infinity = java.lang.Double.POSITIVE_INFINITY;
  // Create the variables x and y.
  MPVariable x = solver.makeNumVar(0.0, infinity, "x");
  MPVariable y = solver.makeNumVar(0.0, infinity, "y");
  
  System.out.println("Number of variables = " + solver.numVariables());

  C#

  // Create the variables x and y.
  Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
  Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");
  
  Console.WriteLine("Number of variables = " + solver.NumVariables());

אחרי שתבצעו את השינויים האלה ותפעילו שוב את התוכנית, תקבלו את הפלט הבא:

Number of variables = 2
Number of constraints = 2
Objective value = 25.000000
x = 0.000000
y = 2.500000

הפתרון לבעיה הלינארית מתרחש בנקודה x = 0, y = 2.5, שבה פונקציית היעד שווה 25. לפניכם גרף שמראה את הפתרונות גם לבעיה הלינארית וגם לבעיה עם המספרים השלמים.

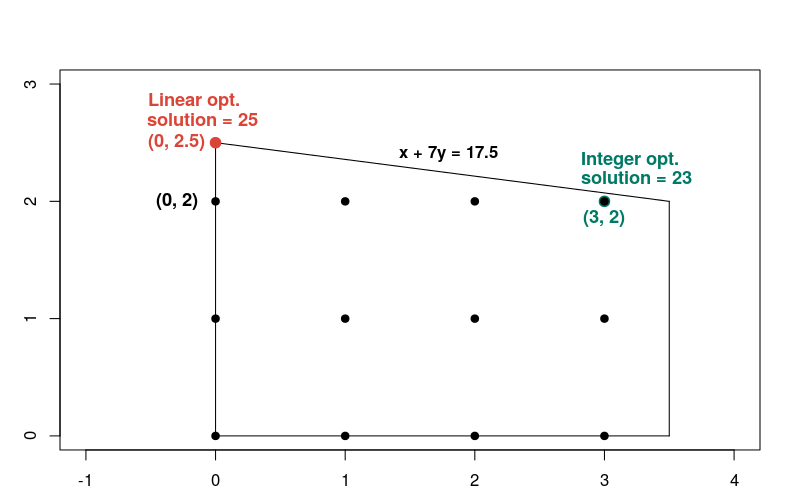
שימו לב שהפתרון עם המספר השלם לא קרוב לפתרון הלינארי, בהשוואה לרוב שאר הנקודות במספרים השלמים באזור האפשרי. באופן כללי, הפתרונות לבעיית אופטימיזציה לינארית ובעיות האופטימיזציה עם המספרים השלמים יכולים להיות רחוקים זה מזה. לכן שני סוגי הבעיות דורשות שיטות שונות לפתרון.