In questa sezione viene mostrato un esempio che mostra come risolvere il problema del viaggiatore per le località mostrate sulla mappa di seguito.
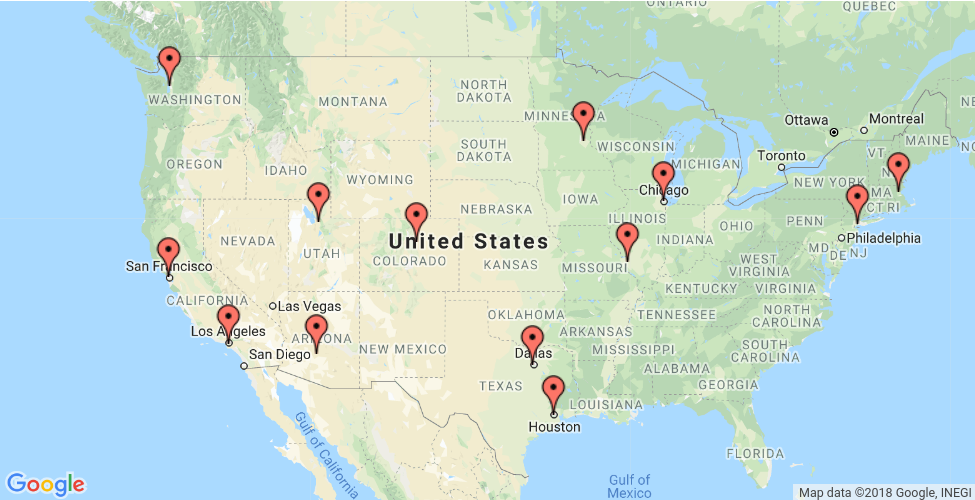
Le seguenti sezioni presentano i programmi in Python, C++, Java e C# che risolvono il TSP utilizzando OR-Tools
Creare i dati
Il codice seguente crea i dati per il problema.
Python
def create_data_model():
"""Stores the data for the problem."""
data = {}
data["distance_matrix"] = [
[0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
[2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
[713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
[1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
[1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
[1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
[2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
[213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
[2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
[875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
[1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
[2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
[1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0],
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
C++
struct DataModel {
const std::vector<std::vector<int64_t>> distance_matrix{
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
Java
static class DataModel {
public final long[][] distanceMatrix = {
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
public final int vehicleNumber = 1;
public final int depot = 0;
}
C#
class DataModel
{
public long[,] DistanceMatrix = {
{ 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 },
{ 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 },
{ 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 },
{ 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 },
{ 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 },
{ 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 },
{ 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 },
{ 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 },
{ 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 },
{ 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 },
{ 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 },
{ 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 },
{ 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
La matrice della distanza è un array la cui voce i, j è la distanza dalla località i alla località j in miglia, dove gli indici dell'array corrispondono alle località nel seguente ordine:
0. New York - 1. Los Angeles - 2. Chicago - 3. Minneapolis - 4. Denver - 5. Dallas
- 6. Seattle - 7. Boston - 8. San Francisco - 9. St. Louis - 10. Houston - 11. Phoenix - 12. Salt Lake City
I dati includono inoltre:
- Il numero di veicoli nel problema, che è 1 perché è un TSP. (Per un problema di percorso del veicolo (VRP), il numero di veicoli può essere maggiore di 1).
- Il depot: la posizione di partenza e quella di arrivo del percorso. In questo caso, il deposito è 0, che corrisponde a New York.
Altri modi per creare la matrice delle distanze
In questo esempio, la matrice delle distanze viene definita in modo esplicito nel programma. È anche possibile utilizzare una funzione per calcolare le distanze tra le posizioni: ad esempio, la formula euclidea per la distanza tra punti nel piano. Tuttavia, è ancora più efficiente precalcolare tutte le distanze tra località e archiviarle in una matrice, anziché calcolarle in fase di esecuzione. Consulta Esempio: forare una scheda per circuiti per un esempio che crea la matrice di distanza in questo modo.
Un'alternativa consiste nell'utilizzare l'API Google Maps Distance Matrix per creare dinamicamente una matrice della distanza (o del tempo di percorrenza) per un problema di percorso.
Crea il modello di routing
Il seguente codice nella sezione principale dei programmi crea il gestore dell'indice (manager) e il modello di routing (routing). Il metodo manager.IndexToNode converte gli indici interni del risolutore (che puoi ignorare in sicurezza) nei numeri per le posizioni. I numeri delle posizioni corrispondono agli indici della matrice delle distanze.
Python
data = create_data_model()
manager = pywrapcp.RoutingIndexManager(
len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
)
routing = pywrapcp.RoutingModel(manager)
C++
DataModel data;
RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles,
data.depot);
RoutingModel routing(manager);
Java
final DataModel data = new DataModel();
RoutingIndexManager manager =
new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);
RoutingModel routing = new RoutingModel(manager);
C#
DataModel data = new DataModel();
RoutingIndexManager manager =
new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot);
RoutingModel routing = new RoutingModel(manager);
Gli input per RoutingIndexManager sono:
- Il numero di righe della matrice, ovvero il numero di località (incluso il deposito).
- Il numero di veicoli interessati dal problema.
- Il nodo corrispondente al deposito.
Creare il callback della distanza
Per utilizzare il risolutore di routing, devi creare un callout a distanza (o trasporto pubblico): una funzione che acquisisca qualsiasi coppia di località e restituisca la distanza tra loro. Il modo più semplice per farlo è utilizzare la matrice delle distanze.
La seguente funzione crea il callback e lo registra con il risolutore come
transit_callback_index.
Python
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data["distance_matrix"][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
C++
const int transit_callback_index = routing.RegisterTransitCallback(
[&data, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return data.distance_matrix[from_node][to_node];
});
Java
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return data.distanceMatrix[fromNode][toNode];
});
C#
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return data.DistanceMatrix[fromNode, toNode];
});
The callback accepts two indices, from_index and to_index, and returns the
corresponding entry of the distance matrix.
Set the cost of travel
The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.
Python
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
In questo esempio, il valutatore del costo dell'arco è transit_callback_index, che è il riferimento interno del risolutore al callback della distanza. Ciò significa che il costo del viaggio tra due località è solo la distanza tra loro.
Tuttavia, in generale, i costi possono coinvolgere anche altri fattori.
Puoi anche definire più valutatori dei costi dell'arco che dipendono dal veicolo che sta passando tra le varie località, utilizzando il metodo routing.SetArcCostEvaluatorOfVehicle().
Ad esempio, se i veicoli hanno velocità diverse, puoi definire il costo del viaggio tra i luoghi in modo che corrisponda alla distanza diviso per la velocità del veicolo, ovvero il tempo di percorrenza.
Imposta parametri di ricerca
Il seguente codice imposta i parametri di ricerca predefiniti e un metodo euristico per trovare la prima soluzione:
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
Java
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
C#
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
Il codice imposta la prima strategia di soluzione su PATH_CHEAPEST_ARC, che crea una route iniziale per il risolutore aggiungendo ripetutamente i bordi con la ponderazione minima che non portano a un nodo visitato in precedenza (diverso dal deposito). Per altre opzioni, consulta la Strategia per la prima soluzione.
Aggiungi la stampante della soluzione
Di seguito è riportata la funzione che mostra la soluzione restituita dal risolutore. La funzione estrae il percorso dalla soluzione e la stampa nella console.
Python
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()} miles")
index = routing.Start(0)
plan_output = "Route for vehicle 0:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Route distance: {route_distance}miles\n"
C++
//! @brief Print the solution.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
// Inspect solution.
LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles";
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
Java
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue() + "miles");
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance + "miles");
}
C#
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}miles", routeDistance);
}
La funzione visualizza il percorso ottimale e la relativa distanza, che è data da ObjectiveValue().
Risolvi e stampa la soluzione
Infine, puoi chiamare il risolutore e stampare la soluzione:
Python
solution = routing.SolveWithParameters(search_parameters)
if solution:
print_solution(manager, routing, solution)
C++
const Assignment* solution = routing.SolveWithParameters(searchParameters); PrintSolution(manager, routing, *solution);
Java
Assignment solution = routing.solveWithParameters(searchParameters); printSolution(routing, manager, solution);
C#
Assignment solution = routing.SolveWithParameters(searchParameters); PrintSolution(routing, manager, solution);
Questo restituisce la soluzione e visualizza il percorso ottimale.
Eseguire i programmi
I programmi che eseguono vengono visualizzati nel seguente output.
Objective: 7293 miles Route for vehicle 0: 0 -> 7 -> 2 -> 3 -> 4 -> 12 -> 6 -> 8 -> 1 -> 11 -> 10 -> 5 -> 9 -> 0
In questo esempio è presente un solo percorso perché è un TSP. Tuttavia, in caso di problemi generali di percorso per il veicolo, la soluzione contiene più route.
Salvare route su un elenco o un array
Invece di stampare direttamente la soluzione, puoi salvare il percorso (o i percorsi per un VRP) in un elenco o in un array. Questo offre il vantaggio di rendere disponibili i percorsi nel caso in cui vogliate utilizzarli in un secondo momento. Ad esempio, puoi eseguire il programma più volte con parametri diversi e salvare le route nelle soluzioni restituite in un file per un confronto.
Le seguenti funzioni salvano le route nella soluzione a qualsiasi VRP (forse con più veicoli) come elenco (Python) o array (C++).
Python
def get_routes(solution, routing, manager):
"""Get vehicle routes from a solution and store them in an array."""
# Get vehicle routes and store them in a two dimensional array whose
# i,j entry is the jth location visited by vehicle i along its route.
routes = []
for route_nbr in range(routing.vehicles()):
index = routing.Start(route_nbr)
route = [manager.IndexToNode(index)]
while not routing.IsEnd(index):
index = solution.Value(routing.NextVar(index))
route.append(manager.IndexToNode(index))
routes.append(route)
return routes
C++
std::vector<std::vector<int>> GetRoutes(const Assignment& solution,
const RoutingModel& routing,
const RoutingIndexManager& manager) {
// Get vehicle routes and store them in a two dimensional array, whose
// i, j entry is the node for the jth visit of vehicle i.
std::vector<std::vector<int>> routes(manager.num_vehicles());
// Get routes.
for (int vehicle_id = 0; vehicle_id < manager.num_vehicles(); ++vehicle_id) {
int64_t index = routing.Start(vehicle_id);
routes[vehicle_id].push_back(manager.IndexToNode(index).value());
while (!routing.IsEnd(index)) {
index = solution.Value(routing.NextVar(index));
routes[vehicle_id].push_back(manager.IndexToNode(index).value());
}
}
return routes;
}
Puoi utilizzare queste funzioni per ottenere i percorsi in qualsiasi esempio VRP nella sezione Routing.
Il codice seguente mostra i percorsi.
Python
routes = get_routes(solution, routing, manager)
# Display the routes.
for i, route in enumerate(routes):
print('Route', i, route)
C++
const std::vector⟨std::vector⟨int⟩⟩
routes = GetRoutes(*solution,
routing,
manager);
// Display the routes.
for (int vehicle_id = 0; vehicle_id < routes.size(); ++vehicle_id) {
LOG(INFO) << "Route " << vehicle_id;
for (int j = 1; j < routes[vehicle_id].size(); ++j) {
LOG(INFO) << routes[vehicle_id][j];
}
}
Per l'esempio corrente, questo codice restituisce il seguente percorso:
Route 0 [0, 7, 2, 3, 4, 12, 6, 8, 1, 11, 10, 5, 9, 0]
Come esercizio, modifica il codice sopra per formattare l'output esattamente come la stampante di soluzione per il programma.
Completare i programmi
Di seguito sono riportati i programmi TSP completi.
Python
"""Simple Travelling Salesperson Problem (TSP) between cities."""
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
data["distance_matrix"] = [
[0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
[2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
[713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
[1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
[1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
[1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
[2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
[213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
[2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
[875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
[1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
[2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
[1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0],
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()} miles")
index = routing.Start(0)
plan_output = "Route for vehicle 0:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Route distance: {route_distance}miles\n"
def main():
"""Entry point of the program."""
# Instantiate the data problem.
data = create_data_model()
# Create the routing index manager.
manager = pywrapcp.RoutingIndexManager(
len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
)
# Create Routing Model.
routing = pywrapcp.RoutingModel(manager)
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data["distance_matrix"][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Setting first solution heuristic.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
# Solve the problem.
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(manager, routing, solution)
if __name__ == "__main__":
main()
C++
#include <cmath>
#include <cstdint>
#include <sstream>
#include <vector>
#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"
namespace operations_research {
struct DataModel {
const std::vector<std::vector<int64_t>> distance_matrix{
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
//! @brief Print the solution.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
// Inspect solution.
LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles";
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
void Tsp() {
// Instantiate the data problem.
DataModel data;
// Create Routing Index Manager
RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles,
data.depot);
// Create Routing Model.
RoutingModel routing(manager);
const int transit_callback_index = routing.RegisterTransitCallback(
[&data, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return data.distance_matrix[from_node][to_node];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
// Solve the problem.
const Assignment* solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(manager, routing, *solution);
}
} // namespace operations_research
int main(int /*argc*/, char* /*argv*/[]) {
operations_research::Tsp();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;
/** Minimal TSP using distance matrix. */
public class TspCities {
private static final Logger logger = Logger.getLogger(TspCities.class.getName());
static class DataModel {
public final long[][] distanceMatrix = {
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
public final int vehicleNumber = 1;
public final int depot = 0;
}
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue() + "miles");
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance + "miles");
}
public static void main(String[] args) throws Exception {
Loader.loadNativeLibraries();
// Instantiate the data problem.
final DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Create and register a transit callback.
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return data.distanceMatrix[fromNode][toNode];
});
// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
// Solve the problem.
Assignment solution = routing.solveWithParameters(searchParameters);
// Print solution on console.
printSolution(routing, manager, solution);
}
}
C#
using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;
/// <summary>
/// Minimal TSP using distance matrix.
/// </summary>
public class TspCities
{
class DataModel
{
public long[,] DistanceMatrix = {
{ 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 },
{ 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 },
{ 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 },
{ 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 },
{ 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 },
{ 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 },
{ 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 },
{ 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 },
{ 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 },
{ 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 },
{ 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 },
{ 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 },
{ 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}miles", routeDistance);
}
public static void Main(String[] args)
{
// Instantiate the data problem.
DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return data.DistanceMatrix[fromNode, toNode];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
// Solve the problem.
Assignment solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(routing, manager, solution);
}
}
Esempio: foratura di un circuito stampato
L'esempio successivo riguarda la creazione di fori in un circuito con un trapano automatizzato. Il problema è trovare la strada più corta che il trapano deve seguire per poter praticare tutti i fori necessari. L'esempio è tratto da TSPLIB, una libreria di problemi TSP.
Ecco un grafico a dispersione delle posizioni dei fori:
Le seguenti sezioni presentano programmi che trovano una buona soluzione per il problema del circuito utilizzando i parametri di ricerca predefiniti del risolutore. Successivamente, ti mostreremo come trovare una soluzione migliore cambiando la strategia di ricerca.
Creare i dati
I dati per il problema sono composti da 280 punti nel piano, mostrati nel grafico a dispersione riportato sopra. Il programma crea i dati in un array di coppie ordinate corrispondenti ai punti nel piano, come mostrato di seguito.
Python
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Locations in block units
data["locations"] = [
# fmt: off
(288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157),
(236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169),
(196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145),
(156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169),
(156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153),
(104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165),
(56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129),
(56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153),
(40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145),
(32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113),
(56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89),
(16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81),
(8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41),
(24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73),
(32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43),
(44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17),
(24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25),
(56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49),
(48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73),
(56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105),
(104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145),
(124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137),
(164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93),
(172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53),
(172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85),
(124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101),
(104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41),
(104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9),
(64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49),
(104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61),
(124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21),
(124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9),
(156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37),
(172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57),
(212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69),
(236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45),
(228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21),
(252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61),
(260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53),
(284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93),
(284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85),
(268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85),
(228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109),
(228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101),
(188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125),
(196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145),
(246, 141), (252, 125), (260, 129), (280, 133)
# fmt: on
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
C++
struct DataModel {
const std::vector<std::vector<int>> locations{
{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157},
{236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145},
{156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169},
{156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153},
{104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165},
{56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129},
{56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153},
{40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145},
{32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113},
{56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89},
{16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81},
{8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41},
{24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73},
{32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43},
{44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17},
{24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25},
{56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49},
{48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73},
{56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105},
{104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137},
{164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93},
{172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53},
{172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85},
{124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101},
{104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41},
{104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9},
{64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61},
{124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21},
{124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9},
{156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57},
{212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69},
{236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45},
{228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61},
{260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53},
{284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93},
{284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85},
{228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109},
{228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101},
{188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125},
{196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145},
{246, 141}, {252, 125}, {260, 129}, {280, 133},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
Java
static class DataModel {
public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157},
{246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145},
{148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169},
{132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165},
{80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137},
{56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161},
{40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121},
{32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89},
{24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65},
{8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65},
{32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27},
{32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17},
{56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57},
{56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97},
{104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137},
{172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77},
{180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81},
{148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89},
{104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17},
{92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53},
{124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9},
{148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73},
{228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53},
{236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77},
{276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77},
{284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93},
{236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125},
{212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109},
{180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145},
{236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}};
public final int vehicleNumber = 1;
public final int depot = 0;
}
C#
class DataModel
{
public int[,] Locations = {
{ 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 },
{ 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 },
{ 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 },
{ 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 },
{ 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 },
{ 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 },
{ 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 },
{ 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 },
{ 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 },
{ 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 },
{ 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 },
{ 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 },
{ 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 },
{ 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 },
{ 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 },
{ 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 },
{ 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 },
{ 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 },
{ 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 },
{ 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 },
{ 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 },
{ 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 },
{ 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 },
{ 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 },
{ 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 },
{ 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 },
{ 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 },
{ 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 },
{ 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 },
{ 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 },
{ 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 },
{ 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 },
{ 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 },
{ 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 },
{ 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 },
{ 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 },
{ 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 },
{ 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 },
{ 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 },
{ 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
Calcola la matrice delle distanze
La funzione riportata di seguito calcola la distanza euclidea tra due punti nei dati e la archivia in un array. Poiché il risolutore di routing funziona sui numeri interi, la funzione arrotonda le distanze calcolate a numeri interi. L'arrotondamento non influisce sulla soluzione in questo esempio, ma potrebbe essere in altri casi. Consulta la pagina Ridimensionare la matrice delle distanze per evitare problemi di arrotondamento.
Python
def compute_euclidean_distance_matrix(locations):
"""Creates callback to return distance between points."""
distances = {}
for from_counter, from_node in enumerate(locations):
distances[from_counter] = {}
for to_counter, to_node in enumerate(locations):
if from_counter == to_counter:
distances[from_counter][to_counter] = 0
else:
# Euclidean distance
distances[from_counter][to_counter] = int(
math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1]))
)
return distances
C++
// @brief Generate distance matrix.
std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix(
const std::vector<std::vector<int>>& locations) {
std::vector<std::vector<int64_t>> distances =
std::vector<std::vector<int64_t>>(
locations.size(), std::vector<int64_t>(locations.size(), int64_t{0}));
for (int from_node = 0; from_node < locations.size(); from_node++) {
for (int to_node = 0; to_node < locations.size(); to_node++) {
if (from_node != to_node)
distances[from_node][to_node] = static_cast<int64_t>(
std::hypot((locations[to_node][0] - locations[from_node][0]),
(locations[to_node][1] - locations[from_node][1])));
}
}
return distances;
}
Java
/// @brief Compute Euclidean distance matrix from locations array.
/// @details It uses an array of locations and computes
/// the Euclidean distance between any two locations.
private static long[][] computeEuclideanDistanceMatrix(int[][] locations) {
// Calculate distance matrix using Euclidean distance.
long[][] distanceMatrix = new long[locations.length][locations.length];
for (int fromNode = 0; fromNode < locations.length; ++fromNode) {
for (int toNode = 0; toNode < locations.length; ++toNode) {
if (fromNode == toNode) {
distanceMatrix[fromNode][toNode] = 0;
} else {
distanceMatrix[fromNode][toNode] =
(long) Math.hypot(locations[toNode][0] - locations[fromNode][0],
locations[toNode][1] - locations[fromNode][1]);
}
}
}
return distanceMatrix;
}
C#
/// <summary>
/// Euclidean distance implemented as a callback. It uses an array of
/// positions and computes the Euclidean distance between the two
/// positions of two different indices.
/// </summary>
static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations)
{
// Calculate the distance matrix using Euclidean distance.
int locationNumber = locations.GetLength(0);
long[,] distanceMatrix = new long[locationNumber, locationNumber];
for (int fromNode = 0; fromNode < locationNumber; fromNode++)
{
for (int toNode = 0; toNode < locationNumber; toNode++)
{
if (fromNode == toNode)
distanceMatrix[fromNode, toNode] = 0;
else
distanceMatrix[fromNode, toNode] =
(long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) +
Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2));
}
}
return distanceMatrix;
}
Aggiungere il callback della distanza
Il codice che crea il callback di distanza è quasi identico a quello dell'esempio precedente. Tuttavia, in questo caso il programma chiama la funzione che calcola la matrice delle distanze prima di aggiungere il callback.
Python
distance_matrix = compute_euclidean_distance_matrix(data["locations"])
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return distance_matrix[from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations);
const int transit_callback_index = routing.RegisterTransitCallback(
[&distance_matrix, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return distance_matrix[from_node][to_node];
});
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations);
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return distanceMatrix[fromNode][toNode];
});
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return distanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
Stampante di soluzioni
La seguente funzione stampa la soluzione nella console. Per mantenere l'output più compatto, la funzione mostra solo gli indici delle località nel percorso.
Python
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()}")
index = routing.Start(0)
plan_output = "Route:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Objective: {route_distance}m\n"
C++
//! @brief Print the solution
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
LOG(INFO) << "Objective: " << solution.ObjectiveValue();
// Inspect solution.
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
Java
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue());
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance);
}
C#
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0}", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}m", routeDistance);
}
Funzione principale
La funzione principale è sostanzialmente la stessa dell'esempio precedente, ma include anche una chiamata alla funzione che crea la matrice delle distanze.
Esecuzione del programma
I programmi completi sono indicati nella sezione successiva. Quando esegui il programma, viene visualizzato il seguente percorso:
Total distance: 2790 Route of vehicle 0: 0 -> 1 -> 279 -> 2 -> 278 -> 277 -> 247 -> 248 -> 249 -> 246 -> 244 -> 243 -> 242 -> 241 -> 240 -> 239 -> 238 -> 237 -> 236 -> 235 -> 234 -> 233 -> 232 -> 231 -> 230 -> 245 -> 250 -> 229 -> 228 -> 227 -> 226 -> 225 -> 224 -> 223 -> 222 -> 221 -> 220 -> 219 -> 218 -> 217 -> 216 -> 215 -> 214 -> 213 -> 212 -> 211 -> 210 -> 209 -> 208 -> 251 -> 254 -> 255 -> 257 -> 256 -> 253 -> 252 -> 207 -> 206 -> 205 -> 204 -> 203 -> 202 -> 142 -> 141 -> 146 -> 147 -> 140 -> 139 -> 265 -> 136 -> 137 -> 138 -> 148 -> 149 -> 177 -> 176 -> 175 -> 178 -> 179 -> 180 -> 181 -> 182 -> 183 -> 184 -> 186 -> 185 -> 192 -> 196 -> 197 -> 198 -> 144 -> 145 -> 143 -> 199 -> 201 -> 200 -> 195 -> 194 -> 193 -> 191 -> 190 -> 189 -> 188 -> 187 -> 163 -> 164 -> 165 -> 166 -> 167 -> 168 -> 169 -> 171 -> 170 -> 172 -> 105 -> 106 -> 104 -> 103 -> 107 -> 109 -> 110 -> 113 -> 114 -> 116 -> 117 -> 61 -> 62 -> 63 -> 65 -> 64 -> 84 -> 85 -> 115 -> 112 -> 86 -> 83 -> 82 -> 87 -> 111 -> 108 -> 89 -> 90 -> 91 -> 102 -> 101 -> 100 -> 99 -> 98 -> 97 -> 96 -> 95 -> 94 -> 93 -> 92 -> 79 -> 88 -> 81 -> 80 -> 78 -> 77 -> 76 -> 74 -> 75 -> 73 -> 72 -> 71 -> 70 -> 69 -> 66 -> 68 -> 67 -> 57 -> 56 -> 55 -> 54 -> 53 -> 52 -> 51 -> 50 -> 49 -> 48 -> 47 -> 46 -> 45 -> 44 -> 43 -> 58 -> 60 -> 59 -> 42 -> 41 -> 40 -> 39 -> 38 -> 37 -> 36 -> 35 -> 34 -> 33 -> 32 -> 31 -> 30 -> 29 -> 124 -> 123 -> 122 -> 121 -> 120 -> 119 -> 118 -> 156 -> 157 -> 158 -> 173 -> 162 -> 161 -> 160 -> 174 -> 159 -> 150 -> 151 -> 155 -> 152 -> 154 -> 153 -> 128 -> 129 -> 130 -> 131 -> 18 -> 19 -> 20 -> 127 -> 126 -> 125 -> 28 -> 27 -> 26 -> 25 -> 21 -> 24 -> 22 -> 23 -> 13 -> 12 -> 14 -> 11 -> 10 -> 9 -> 7 -> 8 -> 6 -> 5 -> 275 -> 274 -> 273 -> 272 -> 271 -> 270 -> 15 -> 16 -> 17 -> 132 -> 133 -> 269 -> 268 -> 134 -> 135 -> 267 -> 266 -> 264 -> 263 -> 262 -> 261 -> 260 -> 258 -> 259 -> 276 -> 3 -> 4 -> 0
Ecco un grafico del percorso corrispondente:
La libreria OR-Tools trova il tour precedente molto rapidamente, in meno di un secondo su un tipico computer. La durata totale del tour precedente è 2790.
Completare i programmi
Ecco i programmi completi per l'esempio di circuito.
Python
"""Simple Travelling Salesperson Problem (TSP) on a circuit board."""
import math
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Locations in block units
data["locations"] = [
# fmt: off
(288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157),
(236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169),
(196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145),
(156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169),
(156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153),
(104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165),
(56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129),
(56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153),
(40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145),
(32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113),
(56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89),
(16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81),
(8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41),
(24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73),
(32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43),
(44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17),
(24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25),
(56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49),
(48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73),
(56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105),
(104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145),
(124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137),
(164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93),
(172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53),
(172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85),
(124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101),
(104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41),
(104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9),
(64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49),
(104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61),
(124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21),
(124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9),
(156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37),
(172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57),
(212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69),
(236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45),
(228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21),
(252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61),
(260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53),
(284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93),
(284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85),
(268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85),
(228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109),
(228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101),
(188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125),
(196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145),
(246, 141), (252, 125), (260, 129), (280, 133)
# fmt: on
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
def compute_euclidean_distance_matrix(locations):
"""Creates callback to return distance between points."""
distances = {}
for from_counter, from_node in enumerate(locations):
distances[from_counter] = {}
for to_counter, to_node in enumerate(locations):
if from_counter == to_counter:
distances[from_counter][to_counter] = 0
else:
# Euclidean distance
distances[from_counter][to_counter] = int(
math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1]))
)
return distances
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()}")
index = routing.Start(0)
plan_output = "Route:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Objective: {route_distance}m\n"
def main():
"""Entry point of the program."""
# Instantiate the data problem.
data = create_data_model()
# Create the routing index manager.
manager = pywrapcp.RoutingIndexManager(
len(data["locations"]), data["num_vehicles"], data["depot"]
)
# Create Routing Model.
routing = pywrapcp.RoutingModel(manager)
distance_matrix = compute_euclidean_distance_matrix(data["locations"])
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return distance_matrix[from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Setting first solution heuristic.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
# Solve the problem.
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(manager, routing, solution)
if __name__ == "__main__":
main()
C++
#include <cmath>
#include <cstdint>
#include <sstream>
#include <vector>
#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"
namespace operations_research {
struct DataModel {
const std::vector<std::vector<int>> locations{
{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157},
{236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145},
{156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169},
{156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153},
{104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165},
{56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129},
{56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153},
{40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145},
{32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113},
{56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89},
{16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81},
{8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41},
{24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73},
{32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43},
{44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17},
{24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25},
{56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49},
{48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73},
{56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105},
{104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137},
{164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93},
{172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53},
{172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85},
{124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101},
{104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41},
{104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9},
{64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61},
{124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21},
{124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9},
{156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57},
{212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69},
{236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45},
{228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61},
{260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53},
{284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93},
{284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85},
{228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109},
{228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101},
{188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125},
{196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145},
{246, 141}, {252, 125}, {260, 129}, {280, 133},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
// @brief Generate distance matrix.
std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix(
const std::vector<std::vector<int>>& locations) {
std::vector<std::vector<int64_t>> distances =
std::vector<std::vector<int64_t>>(
locations.size(), std::vector<int64_t>(locations.size(), int64_t{0}));
for (int from_node = 0; from_node < locations.size(); from_node++) {
for (int to_node = 0; to_node < locations.size(); to_node++) {
if (from_node != to_node)
distances[from_node][to_node] = static_cast<int64_t>(
std::hypot((locations[to_node][0] - locations[from_node][0]),
(locations[to_node][1] - locations[from_node][1])));
}
}
return distances;
}
//! @brief Print the solution
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
LOG(INFO) << "Objective: " << solution.ObjectiveValue();
// Inspect solution.
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
void Tsp() {
// Instantiate the data problem.
DataModel data;
// Create Routing Index Manager
RoutingIndexManager manager(data.locations.size(), data.num_vehicles,
data.depot);
// Create Routing Model.
RoutingModel routing(manager);
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations);
const int transit_callback_index = routing.RegisterTransitCallback(
[&distance_matrix, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return distance_matrix[from_node][to_node];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
// Solve the problem.
const Assignment* solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(manager, routing, *solution);
}
} // namespace operations_research
int main(int /*argc*/, char* /*argv*/[]) {
operations_research::Tsp();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;
/** Minimal TSP. */
public class TspCircuitBoard {
private static final Logger logger = Logger.getLogger(TspCircuitBoard.class.getName());
static class DataModel {
public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157},
{246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145},
{148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169},
{132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165},
{80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137},
{56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161},
{40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121},
{32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89},
{24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65},
{8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65},
{32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27},
{32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17},
{56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57},
{56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97},
{104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137},
{172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77},
{180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81},
{148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89},
{104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17},
{92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53},
{124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9},
{148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73},
{228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53},
{236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77},
{276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77},
{284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93},
{236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125},
{212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109},
{180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145},
{236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}};
public final int vehicleNumber = 1;
public final int depot = 0;
}
/// @brief Compute Euclidean distance matrix from locations array.
/// @details It uses an array of locations and computes
/// the Euclidean distance between any two locations.
private static long[][] computeEuclideanDistanceMatrix(int[][] locations) {
// Calculate distance matrix using Euclidean distance.
long[][] distanceMatrix = new long[locations.length][locations.length];
for (int fromNode = 0; fromNode < locations.length; ++fromNode) {
for (int toNode = 0; toNode < locations.length; ++toNode) {
if (fromNode == toNode) {
distanceMatrix[fromNode][toNode] = 0;
} else {
distanceMatrix[fromNode][toNode] =
(long) Math.hypot(locations[toNode][0] - locations[fromNode][0],
locations[toNode][1] - locations[fromNode][1]);
}
}
}
return distanceMatrix;
}
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue());
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance);
}
public static void main(String[] args) throws Exception {
Loader.loadNativeLibraries();
// Instantiate the data problem.
final DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.locations.length, data.vehicleNumber, data.depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Create and register a transit callback.
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations);
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return distanceMatrix[fromNode][toNode];
});
// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
// Solve the problem.
Assignment solution = routing.solveWithParameters(searchParameters);
// Print solution on console.
printSolution(routing, manager, solution);
}
}
C#
using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;
/// <summary>
/// Minimal TSP.
/// A description of the problem can be found here:
/// http://en.wikipedia.org/wiki/Travelling_salesperson_problem.
/// </summary>
public class TspCircuitBoard
{
class DataModel
{
public int[,] Locations = {
{ 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 },
{ 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 },
{ 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 },
{ 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 },
{ 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 },
{ 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 },
{ 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 },
{ 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 },
{ 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 },
{ 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 },
{ 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 },
{ 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 },
{ 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 },
{ 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 },
{ 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 },
{ 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 },
{ 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 },
{ 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 },
{ 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 },
{ 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 },
{ 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 },
{ 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 },
{ 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 },
{ 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 },
{ 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 },
{ 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 },
{ 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 },
{ 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 },
{ 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 },
{ 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 },
{ 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 },
{ 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 },
{ 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 },
{ 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 },
{ 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 },
{ 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 },
{ 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 },
{ 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 },
{ 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 },
{ 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
/// <summary>
/// Euclidean distance implemented as a callback. It uses an array of
/// positions and computes the Euclidean distance between the two
/// positions of two different indices.
/// </summary>
static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations)
{
// Calculate the distance matrix using Euclidean distance.
int locationNumber = locations.GetLength(0);
long[,] distanceMatrix = new long[locationNumber, locationNumber];
for (int fromNode = 0; fromNode < locationNumber; fromNode++)
{
for (int toNode = 0; toNode < locationNumber; toNode++)
{
if (fromNode == toNode)
distanceMatrix[fromNode, toNode] = 0;
else
distanceMatrix[fromNode, toNode] =
(long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) +
Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2));
}
}
return distanceMatrix;
}
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0}", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}m", routeDistance);
}
public static void Main(String[] args)
{
// Instantiate the data problem.
DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.Locations.GetLength(0), data.VehicleNumber, data.Depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Define cost of each arc.
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return distanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
// Solve the problem.
Assignment solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(routing, manager, solution);
}
}
Cambiare la strategia di ricerca
Il risolutore di routing non restituisce sempre la soluzione ottimale a un TSP, perché i problemi di routing sono non azionabili dal punto di vista computazionale. Ad esempio, la soluzione restituita nell'esempio precedente non è il percorso ottimale.
Per trovare una soluzione migliore, puoi utilizzare una strategia più avanzata, chiamata ricerca guidata locale, che consente al risolutore di ignorare un minimo locale, una soluzione più breve di tutte le route vicine, ma che non è il minimo globale. Dopo essersi allontanato dal minimo locale, il risolutore continua la ricerca.
Gli esempi riportati di seguito mostrano come impostare una ricerca locale guidata per l'esempio di scheda a circuito.
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.local_search_metaheuristic = (
routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)
search_parameters.time_limit.seconds = 30
search_parameters.log_search = True
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_local_search_metaheuristic(
LocalSearchMetaheuristic::GUIDED_LOCAL_SEARCH);
searchParameters.mutable_time_limit()->set_seconds(30);
search_parameters.set_log_search(true);
Java
Aggiungi la seguente istruzione "import" all'inizio del programma:import com.google.protobuf.Duration;Poi imposta i parametri di ricerca come segue:
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.setLocalSearchMetaheuristic(LocalSearchMetaheuristic.Value.GUIDED_LOCAL_SEARCH)
.setTimeLimit(Duration.newBuilder().setSeconds(30).build())
.setLogSearch(true)
.build();
C#
Aggiungi la seguente riga all'inizio del programma:using Google.Protobuf.WellKnownTypes; // DurationPoi imposta i parametri di ricerca come segue:
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
searchParameters.LocalSearchMetaheuristic = LocalSearchMetaheuristic.Types.Value.GuidedLocalSearch;
searchParameters.TimeLimit = new Duration { Seconds = 30 };
searchParameters.LogSearch = true;
Per altre strategie di ricerca locale, consulta Opzioni di ricerca locale.
Gli esempi precedenti abilitano anche il logging per la ricerca. Sebbene il logging non sia richiesto, può essere utile per il debug.
Quando esegui il programma dopo aver apportato le modifiche indicate sopra, viene visualizzata la seguente soluzione, più breve di quella indicata nella sezione precedente.
Objective: 2672 Route: 0 -> 3 -> 276 -> 4 -> 5 -> 6 -> 8 -> 7 -> 9 -> 10 -> 11 -> 14 -> 12 -> 13 -> 23 -> 22 -> 24 -> 21 -> 25 -> 26 -> 27 -> 28 -> 125 -> 126 -> 127 -> 20 -> 19 -> 130 -> 129 -> 128 -> 153 -> 154 -> 152 -> 155 -> 151 -> 150 -> 177 -> 176 -> 175 -> 180 -> 161 -> 160 -> 174 -> 159 -> 158 -> 157 -> 156 -> 118 -> 119 -> 120 -> 121 -> 122 -> 123 -> 124 -> 29 -> 30 -> 31 -> 32 -> 33 -> 34 -> 35 -> 36 -> 37 -> 38 -> 39 -> 40 -> 41 -> 42 -> 59 -> 60 -> 58 -> 43 -> 44 -> 45 -> 46 -> 47 -> 48 -> 49 -> 50 -> 51 -> 52 -> 53 -> 54 -> 55 -> 56 -> 57 -> 67 -> 68 -> 66 -> 69 -> 70 -> 71 -> 72 -> 73 -> 75 -> 74 -> 76 -> 77 -> 78 -> 80 -> 81 -> 88 -> 79 -> 92 -> 93 -> 94 -> 95 -> 96 -> 97 -> 98 -> 99 -> 100 -> 101 -> 102 -> 91 -> 90 -> 89 -> 108 -> 111 -> 87 -> 82 -> 83 -> 86 -> 112 -> 115 -> 85 -> 84 -> 64 -> 65 -> 63 -> 62 -> 61 -> 117 -> 116 -> 114 -> 113 -> 110 -> 109 -> 107 -> 103 -> 104 -> 105 -> 106 -> 173 -> 172 -> 171 -> 170 -> 169 -> 168 -> 167 -> 166 -> 165 -> 164 -> 163 -> 162 -> 187 -> 188 -> 189 -> 190 -> 191 -> 192 -> 185 -> 186 -> 184 -> 183 -> 182 -> 181 -> 179 -> 178 -> 149 -> 148 -> 138 -> 137 -> 136 -> 266 -> 267 -> 135 -> 134 -> 268 -> 269 -> 133 -> 132 -> 131 -> 18 -> 17 -> 16 -> 15 -> 270 -> 271 -> 272 -> 273 -> 274 -> 275 -> 259 -> 258 -> 260 -> 261 -> 262 -> 263 -> 264 -> 265 -> 139 -> 140 -> 147 -> 146 -> 141 -> 142 -> 145 -> 144 -> 198 -> 197 -> 196 -> 193 -> 194 -> 195 -> 200 -> 201 -> 199 -> 143 -> 202 -> 203 -> 204 -> 205 -> 206 -> 207 -> 252 -> 253 -> 256 -> 257 -> 255 -> 254 -> 251 -> 208 -> 209 -> 210 -> 211 -> 212 -> 213 -> 214 -> 215 -> 216 -> 217 -> 218 -> 219 -> 220 -> 221 -> 222 -> 223 -> 224 -> 225 -> 226 -> 227 -> 232 -> 233 -> 234 -> 235 -> 236 -> 237 -> 230 -> 231 -> 228 -> 229 -> 250 -> 245 -> 238 -> 239 -> 240 -> 241 -> 242 -> 243 -> 244 -> 246 -> 249 -> 248 -> 247 -> 277 -> 278 -> 2 -> 279 -> 1 -> 0
Per ulteriori opzioni di ricerca, consulta Opzioni di routing.
Gli algoritmi migliori ora possono risolvere regolarmente le istanze TSP con decine di migliaia di nodi. Il record al momento della stesura è l'istanza pla85900 in TSPLIB, un'applicazione VLSI con 85.900 nodi. Per alcune istanze con milioni di nodi, le soluzioni sono state garantite entro l'1% di un tour ottimale.
Ridimensionamento della matrice delle distanze
Poiché il risolutore di routing funziona sui numeri interi, se la matrice della distanza contiene voci non intere, devi arrotondare le distanze ai numeri interi. Se una certa distanza è ridotta, l'arrotondamento può influire sulla soluzione.
Per evitare problemi con l'arrotondamento, puoi scale la matrice delle distanze: moltiplica
tutte le voci della matrice per un numero elevato, ad esempio 100. Questo moltiplica la lunghezza di qualsiasi route per un fattore 100, ma la soluzione non viene modificata. Il vantaggio è che quando arrotondi le voci della matrice, l'arrotondamento (che è al massimo 0,5) è molto piccolo rispetto alle distanze, quindi non influirà in modo significativo sulla soluzione.
Se scali la matrice delle distanze, devi anche modificare la stampante della soluzione per dividere le lunghezze dei percorsi scalati per il fattore di scalabilità, in modo che mostri le distanze non ridimensionate dei percorsi.
