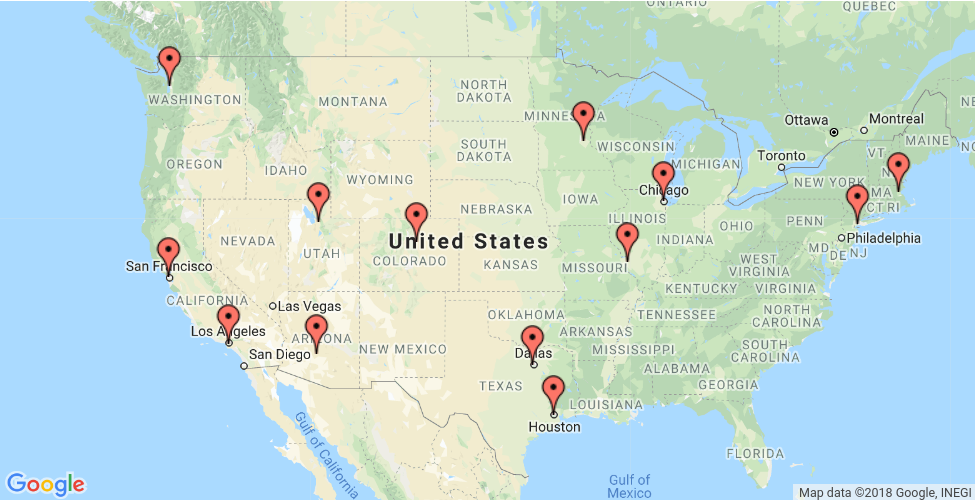
Ta sekcja przedstawia przykład rozwiązania problemu podróżnego sprzedawcy (TSP) w przypadku lokalizacji widocznych na mapie poniżej.
W sekcjach poniżej znajdziesz programy w języku Python, C++, Java i C#, które rozwiązują zadania TSP za pomocą narzędzi OR-Tools.
Tworzenie danych
Kod poniżej tworzy dane problemu.
Python
def create_data_model():
"""Stores the data for the problem."""
data = {}
data["distance_matrix"] = [
[0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
[2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
[713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
[1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
[1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
[1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
[2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
[213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
[2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
[875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
[1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
[2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
[1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0],
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
C++
struct DataModel {
const std::vector<std::vector<int64_t>> distance_matrix{
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
Java
static class DataModel {
public final long[][] distanceMatrix = {
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
public final int vehicleNumber = 1;
public final int depot = 0;
}
C#
class DataModel
{
public long[,] DistanceMatrix = {
{ 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 },
{ 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 },
{ 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 },
{ 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 },
{ 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 },
{ 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 },
{ 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 },
{ 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 },
{ 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 },
{ 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 },
{ 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 },
{ 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 },
{ 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
Tablica odległości to tablica, której wpis i, j to odległość od lokalizacji i do lokalizacji j w milach, gdzie indeksy tablicy odpowiadają lokalizacjom w tej kolejności:
0. New York - 1. Los Angeles - 2. Chicago - 3. Minneapolis - 4. Denver - 5. Dallas
- 6. Seattle - 7. Boston - 8. San Francisco - 9. St. Louis - 10. Houston - 11. Phoenix - 12. Salt Lake City
Dane te obejmują też:
- Liczba pojazdów w problemie, która wynosi 1, ponieważ jest to dostawca usługi tokenów. W przypadku problemu z wyznaczaniem trasy (VRP) liczba pojazdów może być większa niż 1.
- Depot: początek i koniec trasy. W tym przypadku depot ma wartość 0, która odpowiada Nowemu Jorku.
Inne sposoby tworzenia macierzy odległości
W tym przykładzie macierz odległości jest wyraźnie zdefiniowany w programie. Możesz też użyć funkcji do obliczania odległości między lokalizacjami, na przykład formułą Euklidesowa dla odległości między punktami w płaszczyźnie. wydajniejsze jest jednak wstępne obliczanie wszystkich odległości między lokalizacjami i ich zapisywanie w macierzy niż obliczanie ich w czasie działania. Zobacz przykład: wiercenie obwodu drukowanego dla przykładu, który tworzy macierz odległości w ten sposób.
Innym rozwiązaniem jest użycie interfejsu Google Maps Length Matrix API do dynamicznego tworzenia macierzy odległości lub czasu podróży w przypadku problemu z wyznaczanie trasy.
Tworzenie modelu routingu
Ten kod w głównej sekcji programów tworzy menedżera indeksów (manager) i modelu routingu (routing). Metoda manager.IndexToNode konwertuje wewnętrzne indeksy rozwiązania (które można bezpiecznie zignorować) na liczby lokalizacji. Numery lokalizacji odpowiadają indeksom macierzy odległości.
Python
data = create_data_model()
manager = pywrapcp.RoutingIndexManager(
len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
)
routing = pywrapcp.RoutingModel(manager)
C++
DataModel data;
RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles,
data.depot);
RoutingModel routing(manager);
Java
final DataModel data = new DataModel();
RoutingIndexManager manager =
new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);
RoutingModel routing = new RoutingModel(manager);
C#
DataModel data = new DataModel();
RoutingIndexManager manager =
new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot);
RoutingModel routing = new RoutingModel(manager);
Dane wejściowe RoutingIndexManager to:
- Liczba wierszy macierzy odległości, która jest liczbą lokalizacji (w tym magazynu).
- Liczba pojazdów, których dotyczy problem.
- Węzeł odpowiadający zajezdni.
Utwórz wywołanie zwrotne odległości
Aby użyć funkcji rozwiązania do wyznaczania tras, musisz utworzyć wywołanie dystansu (lub transportu publicznego): funkcję, która przyjmuje dowolną parę lokalizacji i zwraca odległość między nimi. Najłatwiej to zrobić za pomocą macierzy odległości.
Poniższa funkcja tworzy wywołanie zwrotne i rejestruje je w resolver jako transit_callback_index.
Python
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data["distance_matrix"][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
C++
const int transit_callback_index = routing.RegisterTransitCallback(
[&data, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return data.distance_matrix[from_node][to_node];
});
Java
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return data.distanceMatrix[fromNode][toNode];
});
C#
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return data.DistanceMatrix[fromNode, toNode];
});
The callback accepts two indices, from_index and to_index, and returns the
corresponding entry of the distance matrix.
Set the cost of travel
The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.
Python
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
W tym przykładzie narzędzie do oceny kosztów łuku zawiera transit_callback_index, które jest wewnętrznym odwołaniem do wywołania zwrotnego odległości. Oznacza to, że koszt podróży między 2 lokalizacjami to jedynie odległość między nimi.
Ogólnie koszty mogą jednak dotyczyć także innych czynników.
Za pomocą metody routing.SetArcCostEvaluatorOfVehicle() możesz też zdefiniować wiele szacatorów kosztu łuku zależnych od tego, który pojazd przemieszcza się między lokalizacjami.
Jeśli na przykład pojazdy mają różne prędkości, możesz zdefiniować koszt podróży między lokalizacjami przez odległość podzieloną przez prędkość pojazdu, czyli czas podróży.
Ustaw parametry wyszukiwania
Ten kod ustawia domyślne parametry wyszukiwania i metodę heurystyczną w celu znalezienia pierwszego rozwiązania:
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
Java
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
C#
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
Kod ustawia pierwszą strategię rozwiązania na PATH_CHEAPEST_ARC, co tworzy początkową ścieżkę dla rozwiązania przez wielokrotne dodawanie krawędzi o najniższym wadze, które nie prowadzą do poprzednio odwiedzonego węzła (innego niż magazyn). Inne opcje znajdziesz w artykule Pierwsza strategia rozwiązania.
Dodawanie drukarki rozwiązania
Poniżej wyświetlana jest funkcja wyświetlająca rozwiązanie zwrócone przez rozwiązanie. Funkcja ta wyodrębnia trasę z rozwiązania i drukuje ją w konsoli.
Python
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()} miles")
index = routing.Start(0)
plan_output = "Route for vehicle 0:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Route distance: {route_distance}miles\n"
C++
//! @brief Print the solution.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
// Inspect solution.
LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles";
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
Java
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue() + "miles");
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance + "miles");
}
C#
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}miles", routeDistance);
}
Ta funkcja wyświetla optymalną trasę i jej odległość, którą podaje ObjectiveValue().
Rozwiązywanie problemów i drukowanie rozwiązania
Na koniec możesz wywołać funkcję rozwiązania i wydrukować rozwiązanie:
Python
solution = routing.SolveWithParameters(search_parameters)
if solution:
print_solution(manager, routing, solution)
C++
const Assignment* solution = routing.SolveWithParameters(searchParameters); PrintSolution(manager, routing, *solution);
Java
Assignment solution = routing.solveWithParameters(searchParameters); printSolution(routing, manager, solution);
C#
Assignment solution = routing.SolveWithParameters(searchParameters); PrintSolution(routing, manager, solution);
Zwraca to rozwiązanie i wyświetla optymalną trasę.
Uruchom programy
Uruchomione programy wyświetlają następujące dane wyjściowe.
Objective: 7293 miles Route for vehicle 0: 0 -> 7 -> 2 -> 3 -> 4 -> 12 -> 6 -> 8 -> 1 -> 11 -> 10 -> 5 -> 9 -> 0
W tym przykładzie jest tylko jedna trasa, ponieważ jest to dostawca usługi tokenów. Jednak w bardziej ogólnych problemach z routingiem pojazdem rozwiązanie zawiera wiele tras.
Zapisywanie tras na liście lub w tablicy
Zamiast drukować rozwiązanie bezpośrednio, możesz zapisać trasę (lub trasy w przypadku VRP) na liście lub w tablicy. Dzięki temu możesz udostępnić te trasy, aby móc z nimi później skorzystać. Możesz na przykład kilkakrotnie uruchomić program z różnymi parametrami i zapisać trasy w zwróconych rozwiązaniach do pliku do porównania.
Poniższe funkcje zapisują trasy w rozwiązaniu do dowolnej platformy VR (prawdopodobnie z wieloma pojazdami) jako listy (Python) lub tablicy (C++).
Python
def get_routes(solution, routing, manager):
"""Get vehicle routes from a solution and store them in an array."""
# Get vehicle routes and store them in a two dimensional array whose
# i,j entry is the jth location visited by vehicle i along its route.
routes = []
for route_nbr in range(routing.vehicles()):
index = routing.Start(route_nbr)
route = [manager.IndexToNode(index)]
while not routing.IsEnd(index):
index = solution.Value(routing.NextVar(index))
route.append(manager.IndexToNode(index))
routes.append(route)
return routes
C++
std::vector<std::vector<int>> GetRoutes(const Assignment& solution,
const RoutingModel& routing,
const RoutingIndexManager& manager) {
// Get vehicle routes and store them in a two dimensional array, whose
// i, j entry is the node for the jth visit of vehicle i.
std::vector<std::vector<int>> routes(manager.num_vehicles());
// Get routes.
for (int vehicle_id = 0; vehicle_id < manager.num_vehicles(); ++vehicle_id) {
int64_t index = routing.Start(vehicle_id);
routes[vehicle_id].push_back(manager.IndexToNode(index).value());
while (!routing.IsEnd(index)) {
index = solution.Value(routing.NextVar(index));
routes[vehicle_id].push_back(manager.IndexToNode(index).value());
}
}
return routes;
}
Korzystając z tych funkcji, możesz uzyskiwać trasy w dowolnych przykładach VRP w sekcji Routing.
Następujący kod zawiera trasy.
Python
routes = get_routes(solution, routing, manager)
# Display the routes.
for i, route in enumerate(routes):
print('Route', i, route)
C++
const std::vector⟨std::vector⟨int⟩⟩
routes = GetRoutes(*solution,
routing,
manager);
// Display the routes.
for (int vehicle_id = 0; vehicle_id < routes.size(); ++vehicle_id) {
LOG(INFO) << "Route " << vehicle_id;
for (int j = 1; j < routes[vehicle_id].size(); ++j) {
LOG(INFO) << routes[vehicle_id][j];
}
}
W bieżącym przykładzie ten kod zwraca tę trasę:
Route 0 [0, 7, 2, 3, 4, 12, 6, 8, 1, 11, 10, 5, 9, 0]
W ramach ćwiczenia zmień powyższy kod, aby sformatować dane wyjściowe tak samo jak drukarkę rozwiązania programu.
Ukończ programy
Pełne programy dla dostawców usług tokenów są pokazane poniżej.
Python
"""Simple Travelling Salesperson Problem (TSP) between cities."""
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
data["distance_matrix"] = [
[0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
[2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
[713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
[1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
[1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
[1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
[2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
[213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
[2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
[875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
[1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
[2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
[1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0],
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()} miles")
index = routing.Start(0)
plan_output = "Route for vehicle 0:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Route distance: {route_distance}miles\n"
def main():
"""Entry point of the program."""
# Instantiate the data problem.
data = create_data_model()
# Create the routing index manager.
manager = pywrapcp.RoutingIndexManager(
len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
)
# Create Routing Model.
routing = pywrapcp.RoutingModel(manager)
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data["distance_matrix"][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Setting first solution heuristic.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
# Solve the problem.
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(manager, routing, solution)
if __name__ == "__main__":
main()
C++
#include <cmath>
#include <cstdint>
#include <sstream>
#include <vector>
#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"
namespace operations_research {
struct DataModel {
const std::vector<std::vector<int64_t>> distance_matrix{
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
//! @brief Print the solution.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
// Inspect solution.
LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles";
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
void Tsp() {
// Instantiate the data problem.
DataModel data;
// Create Routing Index Manager
RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles,
data.depot);
// Create Routing Model.
RoutingModel routing(manager);
const int transit_callback_index = routing.RegisterTransitCallback(
[&data, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return data.distance_matrix[from_node][to_node];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
// Solve the problem.
const Assignment* solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(manager, routing, *solution);
}
} // namespace operations_research
int main(int /*argc*/, char* /*argv*/[]) {
operations_research::Tsp();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;
/** Minimal TSP using distance matrix. */
public class TspCities {
private static final Logger logger = Logger.getLogger(TspCities.class.getName());
static class DataModel {
public final long[][] distanceMatrix = {
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
public final int vehicleNumber = 1;
public final int depot = 0;
}
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue() + "miles");
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance + "miles");
}
public static void main(String[] args) throws Exception {
Loader.loadNativeLibraries();
// Instantiate the data problem.
final DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Create and register a transit callback.
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return data.distanceMatrix[fromNode][toNode];
});
// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
// Solve the problem.
Assignment solution = routing.solveWithParameters(searchParameters);
// Print solution on console.
printSolution(routing, manager, solution);
}
}
C#
using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;
/// <summary>
/// Minimal TSP using distance matrix.
/// </summary>
public class TspCities
{
class DataModel
{
public long[,] DistanceMatrix = {
{ 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 },
{ 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 },
{ 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 },
{ 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 },
{ 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 },
{ 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 },
{ 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 },
{ 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 },
{ 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 },
{ 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 },
{ 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 },
{ 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 },
{ 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}miles", routeDistance);
}
public static void Main(String[] args)
{
// Instantiate the data problem.
DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return data.DistanceMatrix[fromNode, toNode];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
// Solve the problem.
Assignment solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(routing, manager, solution);
}
}
Przykład: wiercenie obwodu drukowanego
Kolejny przykład obejmuje wiercenie otworów w obwodzie drukowanym za pomocą automatycznego odwiertu. Problemem jest znalezienie najkrótszej trasy, w której będzie się wywierać wiertło, aby uzyskać dostęp do wszystkich wymaganych otworów. Przykład pochodzi z biblioteki problemów TSPLIB.
Oto wykres rozproszony w przypadku lokalizacji otworów:
Kolejne sekcje zawierają programy, które pozwalają znaleźć dobre rozwiązanie problemu z obwodem drukowanym przy użyciu domyślnych parametrów wyszukiwania rozwiązania. Następnie pokażemy, jak znaleźć lepsze rozwiązanie przez zmianę strategii wyszukiwania.
Tworzenie danych
Dane problemu obejmują 280 punktów na płaszczyźnie przedstawione na wykresie punktowym powyżej. Program tworzy dane w tablicy par klucz-wartość odpowiadających punktom na płaszczyźnie, jak pokazano poniżej.
Python
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Locations in block units
data["locations"] = [
# fmt: off
(288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157),
(236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169),
(196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145),
(156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169),
(156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153),
(104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165),
(56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129),
(56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153),
(40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145),
(32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113),
(56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89),
(16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81),
(8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41),
(24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73),
(32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43),
(44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17),
(24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25),
(56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49),
(48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73),
(56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105),
(104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145),
(124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137),
(164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93),
(172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53),
(172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85),
(124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101),
(104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41),
(104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9),
(64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49),
(104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61),
(124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21),
(124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9),
(156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37),
(172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57),
(212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69),
(236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45),
(228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21),
(252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61),
(260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53),
(284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93),
(284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85),
(268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85),
(228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109),
(228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101),
(188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125),
(196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145),
(246, 141), (252, 125), (260, 129), (280, 133)
# fmt: on
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
C++
struct DataModel {
const std::vector<std::vector<int>> locations{
{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157},
{236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145},
{156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169},
{156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153},
{104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165},
{56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129},
{56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153},
{40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145},
{32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113},
{56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89},
{16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81},
{8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41},
{24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73},
{32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43},
{44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17},
{24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25},
{56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49},
{48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73},
{56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105},
{104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137},
{164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93},
{172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53},
{172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85},
{124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101},
{104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41},
{104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9},
{64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61},
{124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21},
{124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9},
{156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57},
{212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69},
{236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45},
{228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61},
{260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53},
{284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93},
{284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85},
{228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109},
{228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101},
{188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125},
{196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145},
{246, 141}, {252, 125}, {260, 129}, {280, 133},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
Java
static class DataModel {
public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157},
{246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145},
{148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169},
{132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165},
{80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137},
{56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161},
{40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121},
{32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89},
{24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65},
{8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65},
{32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27},
{32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17},
{56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57},
{56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97},
{104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137},
{172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77},
{180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81},
{148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89},
{104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17},
{92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53},
{124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9},
{148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73},
{228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53},
{236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77},
{276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77},
{284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93},
{236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125},
{212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109},
{180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145},
{236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}};
public final int vehicleNumber = 1;
public final int depot = 0;
}
C#
class DataModel
{
public int[,] Locations = {
{ 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 },
{ 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 },
{ 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 },
{ 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 },
{ 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 },
{ 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 },
{ 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 },
{ 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 },
{ 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 },
{ 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 },
{ 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 },
{ 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 },
{ 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 },
{ 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 },
{ 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 },
{ 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 },
{ 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 },
{ 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 },
{ 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 },
{ 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 },
{ 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 },
{ 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 },
{ 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 },
{ 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 },
{ 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 },
{ 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 },
{ 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 },
{ 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 },
{ 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 },
{ 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 },
{ 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 },
{ 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 },
{ 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 },
{ 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 },
{ 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 },
{ 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 },
{ 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 },
{ 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 },
{ 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 },
{ 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
Oblicz macierz odległości
Funkcja poniżej oblicza odległość euklidesową między dowolnymi dwoma punktami w danych i zapisuje ją w tablicy. Ponieważ rozwiązanie do routingu działa nad liczbami całkowitymi, funkcja zaokrągla obliczone odległości do liczb całkowitych. Zaokrąglanie nie ma wpływu na rozwiązanie w tym przykładzie, ale w innych przypadkach. Aby dowiedzieć się, jak uniknąć możliwych problemów z zaokrągleniem, zapoznaj się z artykułem Skalowanie macierzy odległości.
Python
def compute_euclidean_distance_matrix(locations):
"""Creates callback to return distance between points."""
distances = {}
for from_counter, from_node in enumerate(locations):
distances[from_counter] = {}
for to_counter, to_node in enumerate(locations):
if from_counter == to_counter:
distances[from_counter][to_counter] = 0
else:
# Euclidean distance
distances[from_counter][to_counter] = int(
math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1]))
)
return distances
C++
// @brief Generate distance matrix.
std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix(
const std::vector<std::vector<int>>& locations) {
std::vector<std::vector<int64_t>> distances =
std::vector<std::vector<int64_t>>(
locations.size(), std::vector<int64_t>(locations.size(), int64_t{0}));
for (int from_node = 0; from_node < locations.size(); from_node++) {
for (int to_node = 0; to_node < locations.size(); to_node++) {
if (from_node != to_node)
distances[from_node][to_node] = static_cast<int64_t>(
std::hypot((locations[to_node][0] - locations[from_node][0]),
(locations[to_node][1] - locations[from_node][1])));
}
}
return distances;
}
Java
/// @brief Compute Euclidean distance matrix from locations array.
/// @details It uses an array of locations and computes
/// the Euclidean distance between any two locations.
private static long[][] computeEuclideanDistanceMatrix(int[][] locations) {
// Calculate distance matrix using Euclidean distance.
long[][] distanceMatrix = new long[locations.length][locations.length];
for (int fromNode = 0; fromNode < locations.length; ++fromNode) {
for (int toNode = 0; toNode < locations.length; ++toNode) {
if (fromNode == toNode) {
distanceMatrix[fromNode][toNode] = 0;
} else {
distanceMatrix[fromNode][toNode] =
(long) Math.hypot(locations[toNode][0] - locations[fromNode][0],
locations[toNode][1] - locations[fromNode][1]);
}
}
}
return distanceMatrix;
}
C#
/// <summary>
/// Euclidean distance implemented as a callback. It uses an array of
/// positions and computes the Euclidean distance between the two
/// positions of two different indices.
/// </summary>
static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations)
{
// Calculate the distance matrix using Euclidean distance.
int locationNumber = locations.GetLength(0);
long[,] distanceMatrix = new long[locationNumber, locationNumber];
for (int fromNode = 0; fromNode < locationNumber; fromNode++)
{
for (int toNode = 0; toNode < locationNumber; toNode++)
{
if (fromNode == toNode)
distanceMatrix[fromNode, toNode] = 0;
else
distanceMatrix[fromNode, toNode] =
(long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) +
Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2));
}
}
return distanceMatrix;
}
Dodaj wywołanie zwrotne dystansu
Kod, który tworzy wywołanie zwrotne dystansu, jest prawie taki sam jak w poprzednim przykładzie. Jednak w tym przypadku przed dodaniem wywołania zwrotnego program wywołuje funkcję, która oblicza tablicę odległości.
Python
distance_matrix = compute_euclidean_distance_matrix(data["locations"])
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return distance_matrix[from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations);
const int transit_callback_index = routing.RegisterTransitCallback(
[&distance_matrix, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return distance_matrix[from_node][to_node];
});
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations);
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return distanceMatrix[fromNode][toNode];
});
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return distanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
Drukarka rozwiązania
Poniższa funkcja wyświetla rozwiązanie w konsoli. Aby wyniki były bardziej zwięzłe, funkcja wyświetla tylko indeksy lokalizacji na trasie.
Python
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()}")
index = routing.Start(0)
plan_output = "Route:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Objective: {route_distance}m\n"
C++
//! @brief Print the solution
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
LOG(INFO) << "Objective: " << solution.ObjectiveValue();
// Inspect solution.
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
Java
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue());
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance);
}
C#
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0}", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}m", routeDistance);
}
Główna funkcja
Główna funkcja jest taka sama jak w poprzednim przykładzie, ale zawiera też wywołanie funkcji, która tworzy macierz odległości.
Prowadzenie programu
Pełne programy znajdziesz w następnej sekcji. Po uruchomieniu programu wyświetli się ta trasa:
Total distance: 2790 Route of vehicle 0: 0 -> 1 -> 279 -> 2 -> 278 -> 277 -> 247 -> 248 -> 249 -> 246 -> 244 -> 243 -> 242 -> 241 -> 240 -> 239 -> 238 -> 237 -> 236 -> 235 -> 234 -> 233 -> 232 -> 231 -> 230 -> 245 -> 250 -> 229 -> 228 -> 227 -> 226 -> 225 -> 224 -> 223 -> 222 -> 221 -> 220 -> 219 -> 218 -> 217 -> 216 -> 215 -> 214 -> 213 -> 212 -> 211 -> 210 -> 209 -> 208 -> 251 -> 254 -> 255 -> 257 -> 256 -> 253 -> 252 -> 207 -> 206 -> 205 -> 204 -> 203 -> 202 -> 142 -> 141 -> 146 -> 147 -> 140 -> 139 -> 265 -> 136 -> 137 -> 138 -> 148 -> 149 -> 177 -> 176 -> 175 -> 178 -> 179 -> 180 -> 181 -> 182 -> 183 -> 184 -> 186 -> 185 -> 192 -> 196 -> 197 -> 198 -> 144 -> 145 -> 143 -> 199 -> 201 -> 200 -> 195 -> 194 -> 193 -> 191 -> 190 -> 189 -> 188 -> 187 -> 163 -> 164 -> 165 -> 166 -> 167 -> 168 -> 169 -> 171 -> 170 -> 172 -> 105 -> 106 -> 104 -> 103 -> 107 -> 109 -> 110 -> 113 -> 114 -> 116 -> 117 -> 61 -> 62 -> 63 -> 65 -> 64 -> 84 -> 85 -> 115 -> 112 -> 86 -> 83 -> 82 -> 87 -> 111 -> 108 -> 89 -> 90 -> 91 -> 102 -> 101 -> 100 -> 99 -> 98 -> 97 -> 96 -> 95 -> 94 -> 93 -> 92 -> 79 -> 88 -> 81 -> 80 -> 78 -> 77 -> 76 -> 74 -> 75 -> 73 -> 72 -> 71 -> 70 -> 69 -> 66 -> 68 -> 67 -> 57 -> 56 -> 55 -> 54 -> 53 -> 52 -> 51 -> 50 -> 49 -> 48 -> 47 -> 46 -> 45 -> 44 -> 43 -> 58 -> 60 -> 59 -> 42 -> 41 -> 40 -> 39 -> 38 -> 37 -> 36 -> 35 -> 34 -> 33 -> 32 -> 31 -> 30 -> 29 -> 124 -> 123 -> 122 -> 121 -> 120 -> 119 -> 118 -> 156 -> 157 -> 158 -> 173 -> 162 -> 161 -> 160 -> 174 -> 159 -> 150 -> 151 -> 155 -> 152 -> 154 -> 153 -> 128 -> 129 -> 130 -> 131 -> 18 -> 19 -> 20 -> 127 -> 126 -> 125 -> 28 -> 27 -> 26 -> 25 -> 21 -> 24 -> 22 -> 23 -> 13 -> 12 -> 14 -> 11 -> 10 -> 9 -> 7 -> 8 -> 6 -> 5 -> 275 -> 274 -> 273 -> 272 -> 271 -> 270 -> 15 -> 16 -> 17 -> 132 -> 133 -> 269 -> 268 -> 134 -> 135 -> 267 -> 266 -> 264 -> 263 -> 262 -> 261 -> 260 -> 258 -> 259 -> 276 -> 3 -> 4 -> 0
Oto wykres przedstawiający odpowiednią trasę:
Biblioteka OR-Tools bardzo szybko znajduje powyżej wycieczkę: w mniej niż sekundę na typowym komputerze. Całkowita długość powyższej wycieczki to 2790.
Ukończ programy
Oto pełne programy dotyczące przykładu obwodu drukowanego.
Python
"""Simple Travelling Salesperson Problem (TSP) on a circuit board."""
import math
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Locations in block units
data["locations"] = [
# fmt: off
(288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157),
(236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169),
(196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145),
(156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169),
(156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153),
(104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165),
(56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129),
(56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153),
(40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145),
(32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113),
(56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89),
(16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81),
(8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41),
(24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73),
(32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43),
(44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17),
(24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25),
(56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49),
(48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73),
(56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105),
(104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145),
(124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137),
(164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93),
(172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53),
(172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85),
(124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101),
(104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41),
(104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9),
(64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49),
(104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61),
(124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21),
(124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9),
(156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37),
(172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57),
(212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69),
(236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45),
(228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21),
(252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61),
(260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53),
(284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93),
(284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85),
(268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85),
(228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109),
(228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101),
(188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125),
(196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145),
(246, 141), (252, 125), (260, 129), (280, 133)
# fmt: on
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
def compute_euclidean_distance_matrix(locations):
"""Creates callback to return distance between points."""
distances = {}
for from_counter, from_node in enumerate(locations):
distances[from_counter] = {}
for to_counter, to_node in enumerate(locations):
if from_counter == to_counter:
distances[from_counter][to_counter] = 0
else:
# Euclidean distance
distances[from_counter][to_counter] = int(
math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1]))
)
return distances
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()}")
index = routing.Start(0)
plan_output = "Route:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Objective: {route_distance}m\n"
def main():
"""Entry point of the program."""
# Instantiate the data problem.
data = create_data_model()
# Create the routing index manager.
manager = pywrapcp.RoutingIndexManager(
len(data["locations"]), data["num_vehicles"], data["depot"]
)
# Create Routing Model.
routing = pywrapcp.RoutingModel(manager)
distance_matrix = compute_euclidean_distance_matrix(data["locations"])
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return distance_matrix[from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Setting first solution heuristic.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
# Solve the problem.
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(manager, routing, solution)
if __name__ == "__main__":
main()
C++
#include <cmath>
#include <cstdint>
#include <sstream>
#include <vector>
#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"
namespace operations_research {
struct DataModel {
const std::vector<std::vector<int>> locations{
{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157},
{236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145},
{156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169},
{156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153},
{104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165},
{56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129},
{56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153},
{40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145},
{32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113},
{56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89},
{16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81},
{8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41},
{24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73},
{32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43},
{44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17},
{24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25},
{56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49},
{48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73},
{56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105},
{104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137},
{164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93},
{172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53},
{172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85},
{124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101},
{104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41},
{104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9},
{64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61},
{124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21},
{124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9},
{156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57},
{212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69},
{236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45},
{228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61},
{260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53},
{284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93},
{284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85},
{228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109},
{228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101},
{188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125},
{196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145},
{246, 141}, {252, 125}, {260, 129}, {280, 133},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
// @brief Generate distance matrix.
std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix(
const std::vector<std::vector<int>>& locations) {
std::vector<std::vector<int64_t>> distances =
std::vector<std::vector<int64_t>>(
locations.size(), std::vector<int64_t>(locations.size(), int64_t{0}));
for (int from_node = 0; from_node < locations.size(); from_node++) {
for (int to_node = 0; to_node < locations.size(); to_node++) {
if (from_node != to_node)
distances[from_node][to_node] = static_cast<int64_t>(
std::hypot((locations[to_node][0] - locations[from_node][0]),
(locations[to_node][1] - locations[from_node][1])));
}
}
return distances;
}
//! @brief Print the solution
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
LOG(INFO) << "Objective: " << solution.ObjectiveValue();
// Inspect solution.
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
void Tsp() {
// Instantiate the data problem.
DataModel data;
// Create Routing Index Manager
RoutingIndexManager manager(data.locations.size(), data.num_vehicles,
data.depot);
// Create Routing Model.
RoutingModel routing(manager);
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations);
const int transit_callback_index = routing.RegisterTransitCallback(
[&distance_matrix, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return distance_matrix[from_node][to_node];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
// Solve the problem.
const Assignment* solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(manager, routing, *solution);
}
} // namespace operations_research
int main(int /*argc*/, char* /*argv*/[]) {
operations_research::Tsp();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;
/** Minimal TSP. */
public class TspCircuitBoard {
private static final Logger logger = Logger.getLogger(TspCircuitBoard.class.getName());
static class DataModel {
public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157},
{246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145},
{148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169},
{132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165},
{80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137},
{56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161},
{40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121},
{32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89},
{24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65},
{8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65},
{32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27},
{32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17},
{56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57},
{56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97},
{104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137},
{172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77},
{180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81},
{148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89},
{104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17},
{92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53},
{124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9},
{148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73},
{228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53},
{236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77},
{276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77},
{284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93},
{236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125},
{212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109},
{180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145},
{236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}};
public final int vehicleNumber = 1;
public final int depot = 0;
}
/// @brief Compute Euclidean distance matrix from locations array.
/// @details It uses an array of locations and computes
/// the Euclidean distance between any two locations.
private static long[][] computeEuclideanDistanceMatrix(int[][] locations) {
// Calculate distance matrix using Euclidean distance.
long[][] distanceMatrix = new long[locations.length][locations.length];
for (int fromNode = 0; fromNode < locations.length; ++fromNode) {
for (int toNode = 0; toNode < locations.length; ++toNode) {
if (fromNode == toNode) {
distanceMatrix[fromNode][toNode] = 0;
} else {
distanceMatrix[fromNode][toNode] =
(long) Math.hypot(locations[toNode][0] - locations[fromNode][0],
locations[toNode][1] - locations[fromNode][1]);
}
}
}
return distanceMatrix;
}
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue());
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance);
}
public static void main(String[] args) throws Exception {
Loader.loadNativeLibraries();
// Instantiate the data problem.
final DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.locations.length, data.vehicleNumber, data.depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Create and register a transit callback.
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations);
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return distanceMatrix[fromNode][toNode];
});
// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
// Solve the problem.
Assignment solution = routing.solveWithParameters(searchParameters);
// Print solution on console.
printSolution(routing, manager, solution);
}
}
C#
using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;
/// <summary>
/// Minimal TSP.
/// A description of the problem can be found here:
/// http://en.wikipedia.org/wiki/Travelling_salesperson_problem.
/// </summary>
public class TspCircuitBoard
{
class DataModel
{
public int[,] Locations = {
{ 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 },
{ 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 },
{ 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 },
{ 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 },
{ 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 },
{ 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 },
{ 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 },
{ 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 },
{ 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 },
{ 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 },
{ 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 },
{ 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 },
{ 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 },
{ 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 },
{ 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 },
{ 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 },
{ 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 },
{ 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 },
{ 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 },
{ 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 },
{ 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 },
{ 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 },
{ 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 },
{ 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 },
{ 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 },
{ 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 },
{ 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 },
{ 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 },
{ 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 },
{ 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 },
{ 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 },
{ 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 },
{ 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 },
{ 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 },
{ 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 },
{ 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 },
{ 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 },
{ 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 },
{ 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 },
{ 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
/// <summary>
/// Euclidean distance implemented as a callback. It uses an array of
/// positions and computes the Euclidean distance between the two
/// positions of two different indices.
/// </summary>
static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations)
{
// Calculate the distance matrix using Euclidean distance.
int locationNumber = locations.GetLength(0);
long[,] distanceMatrix = new long[locationNumber, locationNumber];
for (int fromNode = 0; fromNode < locationNumber; fromNode++)
{
for (int toNode = 0; toNode < locationNumber; toNode++)
{
if (fromNode == toNode)
distanceMatrix[fromNode, toNode] = 0;
else
distanceMatrix[fromNode, toNode] =
(long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) +
Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2));
}
}
return distanceMatrix;
}
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0}", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}m", routeDistance);
}
public static void Main(String[] args)
{
// Instantiate the data problem.
DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.Locations.GetLength(0), data.VehicleNumber, data.Depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Define cost of each arc.
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return distanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
// Solve the problem.
Assignment solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(routing, manager, solution);
}
}
Zmiana strategii wyszukiwania
Rozwiązanie routingu nie zawsze zwraca optymalne rozwiązanie TSP, ponieważ problemy z routingiem są skomplikowane komputerowo. Na przykład rozwiązanie zwrócone w poprzednim przykładzie nie jest optymalną metodą.
Aby znaleźć lepsze rozwiązanie, możesz użyć bardziej zaawansowanej strategii wyszukiwania, zwanej przewodnikiem lokalnym, dzięki której narzędzie ucieknie minimalnej stawki minimalnej, która jest krótsza niż wszystkie trasy w pobliżu, ale nie jest globalne. Gdy użytkownik odejdzie od lokalnego minimum, narzędzie do rozwiązywania problemów kontynuuje wyszukiwanie.
Te przykłady pokazują, jak ustawić wyszukiwanie lokalne z przewodnikiem dla przykładowej płytki obwodu drukowanego.
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.local_search_metaheuristic = (
routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)
search_parameters.time_limit.seconds = 30
search_parameters.log_search = True
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_local_search_metaheuristic(
LocalSearchMetaheuristic::GUIDED_LOCAL_SEARCH);
searchParameters.mutable_time_limit()->set_seconds(30);
search_parameters.set_log_search(true);
Java
Dodaj na początku programu te polecenie „import”:import com.google.protobuf.Duration;Następnie ustaw parametry wyszukiwania w ten sposób:
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.setLocalSearchMetaheuristic(LocalSearchMetaheuristic.Value.GUIDED_LOCAL_SEARCH)
.setTimeLimit(Duration.newBuilder().setSeconds(30).build())
.setLogSearch(true)
.build();C#
Dodaj na początku programu ten wiersz:using Google.Protobuf.WellKnownTypes; // DurationNastępnie ustaw parametry wyszukiwania w ten sposób:
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
searchParameters.LocalSearchMetaheuristic = LocalSearchMetaheuristic.Types.Value.GuidedLocalSearch;
searchParameters.TimeLimit = new Duration { Seconds = 30 };
searchParameters.LogSearch = true;Inne strategie wyszukiwania lokalnego znajdziesz w artykule Lokalne opcje wyszukiwania.
W podanych wyżej przykładach można też włączyć rejestrowanie wyszukiwania. Logowanie nie jest wymagane, jednak może być przydatne podczas debugowania.
Po uruchomieniu programu po wprowadzeniu zmian opisanych powyżej otrzymasz następujące rozwiązanie, które jest krótsze niż rozwiązanie przedstawione w poprzedniej sekcji.
Objective: 2672 Route: 0 -> 3 -> 276 -> 4 -> 5 -> 6 -> 8 -> 7 -> 9 -> 10 -> 11 -> 14 -> 12 -> 13 -> 23 -> 22 -> 24 -> 21 -> 25 -> 26 -> 27 -> 28 -> 125 -> 126 -> 127 -> 20 -> 19 -> 130 -> 129 -> 128 -> 153 -> 154 -> 152 -> 155 -> 151 -> 150 -> 177 -> 176 -> 175 -> 180 -> 161 -> 160 -> 174 -> 159 -> 158 -> 157 -> 156 -> 118 -> 119 -> 120 -> 121 -> 122 -> 123 -> 124 -> 29 -> 30 -> 31 -> 32 -> 33 -> 34 -> 35 -> 36 -> 37 -> 38 -> 39 -> 40 -> 41 -> 42 -> 59 -> 60 -> 58 -> 43 -> 44 -> 45 -> 46 -> 47 -> 48 -> 49 -> 50 -> 51 -> 52 -> 53 -> 54 -> 55 -> 56 -> 57 -> 67 -> 68 -> 66 -> 69 -> 70 -> 71 -> 72 -> 73 -> 75 -> 74 -> 76 -> 77 -> 78 -> 80 -> 81 -> 88 -> 79 -> 92 -> 93 -> 94 -> 95 -> 96 -> 97 -> 98 -> 99 -> 100 -> 101 -> 102 -> 91 -> 90 -> 89 -> 108 -> 111 -> 87 -> 82 -> 83 -> 86 -> 112 -> 115 -> 85 -> 84 -> 64 -> 65 -> 63 -> 62 -> 61 -> 117 -> 116 -> 114 -> 113 -> 110 -> 109 -> 107 -> 103 -> 104 -> 105 -> 106 -> 173 -> 172 -> 171 -> 170 -> 169 -> 168 -> 167 -> 166 -> 165 -> 164 -> 163 -> 162 -> 187 -> 188 -> 189 -> 190 -> 191 -> 192 -> 185 -> 186 -> 184 -> 183 -> 182 -> 181 -> 179 -> 178 -> 149 -> 148 -> 138 -> 137 -> 136 -> 266 -> 267 -> 135 -> 134 -> 268 -> 269 -> 133 -> 132 -> 131 -> 18 -> 17 -> 16 -> 15 -> 270 -> 271 -> 272 -> 273 -> 274 -> 275 -> 259 -> 258 -> 260 -> 261 -> 262 -> 263 -> 264 -> 265 -> 139 -> 140 -> 147 -> 146 -> 141 -> 142 -> 145 -> 144 -> 198 -> 197 -> 196 -> 193 -> 194 -> 195 -> 200 -> 201 -> 199 -> 143 -> 202 -> 203 -> 204 -> 205 -> 206 -> 207 -> 252 -> 253 -> 256 -> 257 -> 255 -> 254 -> 251 -> 208 -> 209 -> 210 -> 211 -> 212 -> 213 -> 214 -> 215 -> 216 -> 217 -> 218 -> 219 -> 220 -> 221 -> 222 -> 223 -> 224 -> 225 -> 226 -> 227 -> 232 -> 233 -> 234 -> 235 -> 236 -> 237 -> 230 -> 231 -> 228 -> 229 -> 250 -> 245 -> 238 -> 239 -> 240 -> 241 -> 242 -> 243 -> 244 -> 246 -> 249 -> 248 -> 247 -> 277 -> 278 -> 2 -> 279 -> 1 -> 0
Więcej opcji wyszukiwania znajdziesz w artykule Opcje routingu.
Najlepsze algorytmy mogą teraz regularnie rozwiązywać problemy instancji TSP z dziesiątkami tysięcy węzłów. Rekord w momencie zapisu to instancja pla85900 w TSPLIB, aplikacji VLSI z 85 900 węzłami. W przypadku niektórych instancji obejmujących miliony węzłów rozwiązania pewnie nie przekraczają 1% optymalnej prezentacji.
Skalowanie macierzy odległości
Rozwiązanie do routingu działa nad liczbami całkowitymi, więc jeśli macierz odległości ma wpisy inne niż całkowite, dystanse muszą być zaokrąglane do liczb całkowitych. Jeśli niektóre odległości są małe, zaokrąglanie może mieć wpływ na rozwiązanie.
Aby uniknąć problemów z zaokrąglaniem, możesz scale macierz odległości: mnożyć wszystkie wpisy macierzy przez większą liczbę, np. 100. Powoduje to pomnożenie długości dowolnej trasy przez 100, ale nie powoduje zmiany rozwiązania. Zaletą jest to, że teraz, gdy zaokrąglisz wpisy macierzy, zaokrąglona wartość (maksymalnie 0,5) jest bardzo mała w porównaniu z odległościami, więc nie wpłynie to znacząco na rozwiązanie.
Jeśli skalujesz macierz odległości, musisz też zmienić drukarkę rozwiązania, aby podzielić skalowane długości tras przez współczynnik skalowania, tak aby wyświetlała nieskalowane odległości.
