در بخشهای بعدی، برنامهنویسی محدودیت (CP) را با یک مسئله ترکیبی بر اساس بازی شطرنج نشان خواهیم داد. در شطرنج، یک ملکه می تواند به صورت افقی، عمودی و مورب حمله کند. مسئله N-queens می پرسد:
چگونه می توان N ملکه را روی صفحه شطرنج NxN قرار داد تا هیچ دو نفر از آنها به یکدیگر حمله نکنند؟
در زیر، می توانید یک راه حل ممکن برای مسئله N-queens برای N = 4 را مشاهده کنید.
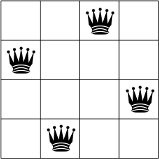
هیچ دو ملکه روی یک ردیف، ستون یا مورب یکسان نیستند.
توجه داشته باشید که این یک مشکل بهینهسازی نیست: ما میخواهیم همه راهحلهای ممکن را پیدا کنیم، نه یک راهحل بهینه، که آن را به یک نامزد طبیعی برای برنامهنویسی محدودیت تبدیل میکند. بخشهای زیر رویکرد CP را برای مسئله N-queens شرح میدهند و برنامههایی را ارائه میکنند که آن را با استفاده از حلکننده CP-SAT و حلکننده اصلی CP حل میکنند.
رویکرد CP به مسئله N-queens
یک حلکننده CP با آزمایش سیستماتیک تمام تخصیصهای ممکن مقادیر به متغیرهای یک مسئله، برای یافتن راهحلهای امکانپذیر کار میکند. در مسئله 4 ملکه، حل کننده از سمت چپ ترین ستون شروع می کند و به طور متوالی یک ملکه را در هر ستون، در مکانی که توسط هیچ ملکه قبلی مورد حمله قرار نمی گیرد، قرار می دهد.
انتشار و عقب نشینی
دو عنصر کلیدی برای جستجوی برنامه نویسی محدودیت وجود دارد:
- انتشار - هر بار که حلکننده مقداری را به یک متغیر اختصاص میدهد، محدودیتها محدودیتهایی را روی مقادیر ممکن متغیرهای تخصیص نیافته اضافه میکنند. این محدودیت ها به تخصیص متغیرهای آینده انتشار می یابد . به عنوان مثال، در مسئله 4 ملکه، هر بار که حل کننده یک ملکه قرار می دهد، نمی تواند ملکه دیگری را روی ردیف و مورب های ملکه فعلی قرار دهد. انتشار می تواند با کاهش مجموعه مقادیر متغیری که حل کننده باید جستجو کند، جستجو را به میزان قابل توجهی افزایش دهد.
- بازگشت به عقب زمانی اتفاق میافتد که یا به دلیل محدودیتها، حلکننده نتواند مقداری را به متغیر بعدی اختصاص دهد یا راهحلی پیدا کند. در هر صورت، حل کننده به مرحله قبلی برمی گردد و مقدار متغیر را در آن مرحله به مقداری تغییر می دهد که قبلاً امتحان نشده است. در مثال 4 ملکه، این به معنای انتقال یک ملکه به یک مربع جدید در ستون فعلی است.
در مرحله بعد، خواهید دید که چگونه برنامه نویسی محدودیت از انتشار و عقبگرد برای حل مسئله 4 ملکه استفاده می کند.
فرض کنید حل کننده با قرار دادن خودسرانه یک ملکه در گوشه سمت چپ بالا شروع می کند. این یک نوع فرضیه است. شاید معلوم شود که هیچ راه حلی با یک ملکه در گوشه سمت چپ بالا وجود ندارد.
با توجه به این فرضیه، چه محدودیت هایی را می توانیم منتشر کنیم؟ یک محدودیت این است که فقط یک ملکه در یک ستون می تواند وجود داشته باشد (X های خاکستری زیر)، و محدودیت دیگر دو ملکه را در یک مورب ممنوع می کند (X های قرمز زیر).
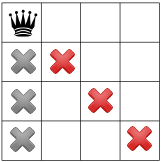
محدودیت سوم ما ملکه ها را در یک ردیف منع می کند:
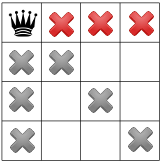
محدودیتهای ما منتشر شد، میتوانیم فرضیه دیگری را آزمایش کنیم و ملکه دوم را روی یکی از مربعهای باقیمانده قرار دهیم. حل کننده ما ممکن است تصمیم بگیرد که اولین مربع موجود در ستون دوم را در آن قرار دهد:
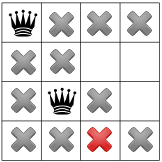
پس از انتشار قید مورب، می بینیم که هیچ مربعی در ستون سوم یا آخرین ردیف باقی نمی گذارد:
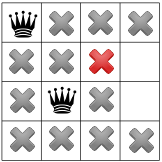
در حالی که هیچ راه حلی در این مرحله ممکن نیست، باید به عقب برگردیم. یکی از گزینه ها این است که حل کننده مربع موجود دیگر را در ستون دوم انتخاب کند. با این حال، انتشار محدودیت سپس یک ملکه را مجبور میکند تا در ردیف دوم ستون سوم قرار گیرد و هیچ نقطه معتبری برای ملکه چهارم باقی نمیگذارد:

و بنابراین، حل کننده باید دوباره به عقب برگردد، این بار تا جایی که اولین ملکه قرار گرفته است. اکنون نشان دادیم که هیچ راه حلی برای مسئله ملکه ها یک مربع گوشه را اشغال نخواهد کرد.
از آنجایی که هیچ ملکه ای در گوشه وجود ندارد، حل کننده ملکه اول را یک به پایین حرکت می دهد و تکثیر می کند و تنها یک نقطه برای ملکه دوم باقی می گذارد:
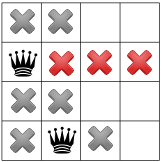
با تکثیر دوباره فقط یک نقطه برای ملکه سوم باقی مانده است:
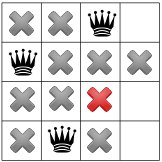
و برای چهارمین و آخرین ملکه:

ما اولین راه حل خود را داریم! اگر به حل کننده خود دستور می دادیم که پس از یافتن اولین راه حل متوقف شود، اینجا تمام می شود. در غیر این صورت، دوباره به عقب برمیگردد و اولین ملکه را در ردیف سوم ستون اول قرار میدهد.
راه حل با استفاده از CP-SAT
مسئله N-queens برای برنامه نویسی محدودیت ها مناسب است. در این بخش، یک برنامه کوتاه پایتون را بررسی می کنیم که از حل کننده CP-SAT برای یافتن همه راه حل های مشکل استفاده می کند.
کتابخانه ها را وارد کنید
کد زیر کتابخانه مورد نیاز را وارد می کند.
پایتون
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
جاوا
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
سی شارپ
using System; using Google.OrTools.Sat;
مدل را اعلام کنید
کد زیر مدل CP-SAT را اعلام می کند.
پایتون
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
جاوا
CpModel model = new CpModel();
سی شارپ
CpModel model = new CpModel();
int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}
// Define constraints.
// All rows must be different.
model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);
// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);
Console.WriteLine("Statistics");
Console.WriteLine($" conflicts : {solver.NumConflicts()}");
Console.WriteLine($" branches : {solver.NumBranches()}");
Console.WriteLine($" wall time : {solver.WallTime()} s");
Console.WriteLine($" number of solutions found: {cb.SolutionCount()}");
}
}
متغیرها را ایجاد کنید
حل کننده متغیرهای مسئله را به صورت آرایه ای به نام queens ایجاد می کند.
پایتون
# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]C++
// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}جاوا
int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}سی شارپ
int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
} در اینجا فرض می کنیم که queens[j] شماره ردیف ملکه در ستون j است. به عبارت دیگر، queens[j] = i یعنی یک ملکه در ردیف i و ستون j وجود دارد.
محدودیت ها را ایجاد کنید
در اینجا کدی است که محدودیت هایی را برای مشکل ایجاد می کند.
پایتون
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(queens[i] + i);
diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);جاوا
// All rows must be different.
model.addAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);سی شارپ
// All rows must be different.
model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2); این کد از متد AddAllDifferent استفاده می کند که نیاز به متفاوت بودن همه عناصر یک آرایه متغیر دارد.
بیایید ببینیم که چگونه این محدودیتها سه شرط را برای مسئله N-queens (ملکهها در ردیفها، ستونها و موربهای مختلف) تضمین میکنند.
دو ملکه در یک ردیف وجود ندارد
اعمال روش AllDifferent حل کننده برای queens ، مقادیر queens[j] مجبور می کند برای هر j متفاوت باشد، به این معنی که همه ملکه ها باید در ردیف های مختلف باشند.
دو ملکه روی یک ستون وجود ندارد
این محدودیت در تعریف queens مستتر است. از آنجایی که هیچ دو عنصر queens نمی توانند شاخص یکسانی داشته باشند، هیچ دو ملکه نمی توانند در یک ستون باشند.
دو ملکه در یک مورب وجود ندارد
محدودیت مورب کمی پیچیده تر از محدودیت های ردیف و ستون است. ابتدا، اگر دو ملکه روی یک مورب دراز بکشند، یکی از شرایط زیر باید درست باشد:
- تعداد ردیف به اضافه شماره ستون برای هر یک از دو ملکه برابر است. به عبارت دیگر،
queens(j) + jبرای دو شاخص مختلفjمقدار یکسانی دارد. - تعداد ردیف منهای تعداد ستون برای هر یک از دو ملکه برابر است. در این مورد،
queens(j) - jبرای دو شاخص مختلفjمقدار یکسانی دارد.
یکی از این شرایط به این معنی است که ملکه ها روی یک مورب صعودی دراز می کشند (از چپ به راست می روند)، در حالی که دیگری به این معنی است که آنها روی همان قطر نزولی دراز می کشند. اینکه کدام شرط مربوط به صعود و کدام حالت نزولی است بستگی به ترتیب ردیف ها و ستون ها دارد. همانطور که در بخش قبل ذکر شد، سفارش هیچ تاثیری بر مجموعه راهحلها ندارد، فقط بر نحوه تجسم آنها.
بنابراین محدودیت مورب این است که مقادیر queens(j) + j همه باید متفاوت باشند، و مقادیر queens(j) - j باید همه متفاوت باشند، برای j مختلف.
برای اعمال متد AddAllDifferent روی queens(j) + j ، N نمونه های متغیر را برای j از 0 تا N-1 در آرایه ای، diag1 ، به صورت زیر قرار می دهیم:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
سپس AddAllDifferent روی diag1 اعمال می کنیم.
model.AddAllDifferent(diag1)
محدودیت برای queens(j) - j به طور مشابه ایجاد می شود.
یک چاپگر راه حل ایجاد کنید
برای چاپ همه راهحلهای مسئله N-queens، باید یک callback به نام چاپگر حل را به حلکننده CP-SAT ارسال کنید. Callback هر راه حل جدید را همانطور که حل کننده آن را پیدا می کند چاپ می کند. کد زیر یک چاپگر راه حل ایجاد می کند.
پایتون
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, queens: list[cp_model.IntVar]):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__queens = queens
self.__solution_count = 0
self.__start_time = time.time()
@property
def solution_count(self) -> int:
return self.__solution_count
def on_solution_callback(self):
current_time = time.time()
print(
f"Solution {self.__solution_count}, "
f"time = {current_time - self.__start_time} s"
)
self.__solution_count += 1
all_queens = range(len(self.__queens))
for i in all_queens:
for j in all_queens:
if self.value(self.__queens[j]) == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
C++
int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (SolutionIntegerValue(response, queens[j]) == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}));جاوا
static class SolutionPrinter extends CpSolverSolutionCallback {
public SolutionPrinter(IntVar[] queensIn) {
solutionCount = 0;
queens = queensIn;
}
@Override
public void onSolutionCallback() {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < queens.length; ++i) {
for (int j = 0; j < queens.length; ++j) {
if (value(queens[j]) == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != queens.length - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
public int getSolutionCount() {
return solutionCount;
}
private int solutionCount;
private final IntVar[] queens;
}سی شارپ
public class SolutionPrinter : CpSolverSolutionCallback
{
public SolutionPrinter(IntVar[] queens)
{
queens_ = queens;
}
public override void OnSolutionCallback()
{
Console.WriteLine($"Solution {SolutionCount_}");
for (int i = 0; i < queens_.Length; ++i)
{
for (int j = 0; j < queens_.Length; ++j)
{
if (Value(queens_[j]) == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != queens_.Length - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount_++;
}
public int SolutionCount()
{
return SolutionCount_;
}
private int SolutionCount_;
private IntVar[] queens_;
}توجه داشته باشید که چاپگر راه حل باید به عنوان یک کلاس پایتون نوشته شود، زیرا رابط پایتون با حل کننده زیرین C++ است.
محلول ها با خطوط زیر در چاپگر محلول چاپ می شوند.
for v in self.__variables:
print('%s = %i' % (v, self.Value(v)), end = ' ') در این مثال self.__variables متغیر queens است و هر v مربوط به یکی از هشت ورودی queens است. این یک راه حل را به شکل زیر چاپ می کند: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) که در آن xi شماره ستون ملکه در ردیف i است.
بخش بعدی نمونه ای از یک راه حل را نشان می دهد.
با حل کننده تماس بگیرید و نتایج را نمایش دهید
کد زیر حل کننده را اجرا می کند و راه حل ها را نمایش می دهد.
پایتون
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
جاوا
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
سی شارپ
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
این برنامه 92 راه حل مختلف برای یک برد 8x8 پیدا می کند. در اینجا اولین مورد است.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92 میتوانید با ارسال N بهعنوان آرگومان خط فرمان، مشکل تختهای با اندازه متفاوت را حل کنید. به عنوان مثال، اگر نام برنامه queens باشد، python nqueens_sat.py 6 مشکل یک برد 6x6 را حل می کند.
کل برنامه
در اینجا کل برنامه برای برنامه N-queens آمده است.
پایتون
"""OR-Tools solution to the N-queens problem."""
import sys
import time
from ortools.sat.python import cp_model
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, queens: list[cp_model.IntVar]):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__queens = queens
self.__solution_count = 0
self.__start_time = time.time()
@property
def solution_count(self) -> int:
return self.__solution_count
def on_solution_callback(self):
current_time = time.time()
print(
f"Solution {self.__solution_count}, "
f"time = {current_time - self.__start_time} s"
)
self.__solution_count += 1
all_queens = range(len(self.__queens))
for i in all_queens:
for j in all_queens:
if self.value(self.__queens[j]) == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
def main(board_size: int) -> None:
# Creates the solver.
model = cp_model.CpModel()
# Creates the variables.
# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
# Creates the constraints.
# All rows must be different.
model.add_all_different(queens)
# No two queens can be on the same diagonal.
model.add_all_different(queens[i] + i for i in range(board_size))
model.add_all_different(queens[i] - i for i in range(board_size))
# Solve the model.
solver = cp_model.CpSolver()
solution_printer = NQueenSolutionPrinter(queens)
solver.parameters.enumerate_all_solutions = True
solver.solve(model, solution_printer)
# Statistics.
print("\nStatistics")
print(f" conflicts : {solver.num_conflicts}")
print(f" branches : {solver.num_branches}")
print(f" wall time : {solver.wall_time} s")
print(f" solutions found: {solution_printer.solution_count}")
if __name__ == "__main__":
# By default, solve the 8x8 problem.
size = 8
if len(sys.argv) > 1:
size = int(sys.argv[1])
main(size)C++
// OR-Tools solution to the N-queens problem.
#include <stdlib.h>
#include <sstream>
#include <string>
#include <vector>
#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"
namespace operations_research {
namespace sat {
void NQueensSat(const int board_size) {
// Instantiate the solver.
CpModelBuilder cp_model;
// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}
// Define constraints.
// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(queens[i] + i);
diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);
int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (SolutionIntegerValue(response, queens[j]) == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}));
// Tell the solver to enumerate all solutions.
SatParameters parameters;
parameters.set_enumerate_all_solutions(true);
model.Add(NewSatParameters(parameters));
const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
LOG(INFO) << "Number of solutions found: " << num_solutions;
// Statistics.
LOG(INFO) << "Statistics";
LOG(INFO) << CpSolverResponseStats(response);
}
} // namespace sat
} // namespace operations_research
int main(int argc, char** argv) {
int board_size = 8;
if (argc > 1) {
if (!absl::SimpleAtoi(argv[1], &board_size)) {
LOG(INFO) << "Cannot parse '" << argv[1]
<< "', using the default value of 8.";
board_size = 8;
}
}
operations_research::sat::NQueensSat(board_size);
return EXIT_SUCCESS;
}جاوا
package com.google.ortools.sat.samples;
import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;
/** OR-Tools solution to the N-queens problem. */
public final class NQueensSat {
static class SolutionPrinter extends CpSolverSolutionCallback {
public SolutionPrinter(IntVar[] queensIn) {
solutionCount = 0;
queens = queensIn;
}
@Override
public void onSolutionCallback() {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < queens.length; ++i) {
for (int j = 0; j < queens.length; ++j) {
if (value(queens[j]) == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != queens.length - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
public int getSolutionCount() {
return solutionCount;
}
private int solutionCount;
private final IntVar[] queens;
}
public static void main(String[] args) {
Loader.loadNativeLibraries();
// Create the model.
CpModel model = new CpModel();
int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}
// Define constraints.
// All rows must be different.
model.addAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);
// Create a solver and solve the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Tell the solver to enumerate all solutions.
solver.getParameters().setEnumerateAllSolutions(true);
// And solve.
solver.solve(model, cb);
// Statistics.
System.out.println("Statistics");
System.out.println(" conflicts : " + solver.numConflicts());
System.out.println(" branches : " + solver.numBranches());
System.out.println(" wall time : " + solver.wallTime() + " s");
System.out.println(" solutions : " + cb.getSolutionCount());
}
private NQueensSat() {}
}سی شارپ
// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.Sat;
public class NQueensSat
{
public class SolutionPrinter : CpSolverSolutionCallback
{
public SolutionPrinter(IntVar[] queens)
{
queens_ = queens;
}
public override void OnSolutionCallback()
{
Console.WriteLine($"Solution {SolutionCount_}");
for (int i = 0; i < queens_.Length; ++i)
{
for (int j = 0; j < queens_.Length; ++j)
{
if (Value(queens_[j]) == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != queens_.Length - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount_++;
}
public int SolutionCount()
{
return SolutionCount_;
}
private int SolutionCount_;
private IntVar[] queens_;
}
static void Main()
{
// Constraint programming engine
CpModel model = new CpModel();
int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}
// Define constraints.
// All rows must be different.
model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);
// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);
Console.WriteLine("Statistics");
Console.WriteLine($" conflicts : {solver.NumConflicts()}");
Console.WriteLine($" branches : {solver.NumBranches()}");
Console.WriteLine($" wall time : {solver.WallTime()} s");
Console.WriteLine($" number of solutions found: {cb.SolutionCount()}");
}
}راه حل با استفاده از حل کننده اصلی CP
بخش های زیر یک برنامه پایتون را ارائه می کند که N-queen ها را با استفاده از حل کننده اصلی CP حل می کند. (با این حال، توصیه می کنیم از حل کننده جدیدتر CP-SAT استفاده کنید)
کتابخانه ها را وارد کنید
کد زیر کتابخانه مورد نیاز را وارد می کند.
پایتون
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
جاوا
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
سی شارپ
using System; using Google.OrTools.ConstraintSolver;
حل کننده را اعلام کنید
کد زیر حل کننده اصلی CP را اعلام می کند.
پایتون
solver = pywrapcp.Solver("n-queens")C++
Solver solver("N-Queens");جاوا
Solver solver = new Solver("N-Queens");سی شارپ
Solver solver = new Solver("N-Queens");متغیرها را ایجاد کنید
متد IntVar حلگر متغیرهای مسئله را به صورت آرایه ای به نام queens ایجاد می کند.
پایتون
# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]C++
std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}جاوا
int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}سی شارپ
const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
} برای هر راه حل، queens[j] = i یعنی یک ملکه در ستون j و ردیف i وجود دارد.
محدودیت ها را ایجاد کنید
در اینجا کدی است که محدودیت هایی را برای مشکل ایجاد می کند.
پایتون
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));
// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));جاوا
// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = solver.makeSum(queens[i], i).var();
diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));سی شارپ
// All rows must be different.
solver.Add(queens.AllDifferent());
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = solver.MakeSum(queens[i], i).Var();
diag2[i] = solver.MakeSum(queens[i], -i).Var();
}
solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());این محدودیتها سه شرط را برای مسئله N-queens تضمین میکنند (ملکهها در ردیفها، ستونها و موربهای مختلف).
دو ملکه در یک ردیف وجود ندارد
اعمال روش AllDifferent حل کننده برای queens ، مقادیر queens[j] مجبور می کند برای هر j متفاوت باشد، به این معنی که همه ملکه ها باید در ردیف های مختلف باشند.
دو ملکه روی یک ستون وجود ندارد
این محدودیت در تعریف queens مستتر است. از آنجایی که هیچ دو عنصر queens نمی توانند شاخص یکسانی داشته باشند، هیچ دو ملکه نمی توانند در یک ستون باشند.
دو ملکه در یک مورب وجود ندارد
محدودیت مورب کمی پیچیده تر از محدودیت های ردیف و ستون است. ابتدا، اگر دو ملکه روی یک مورب دراز بکشند، یکی از موارد زیر باید درست باشد:
- اگر مورب نزولی باشد (از چپ به راست می رود)، تعداد سطر به اضافه شماره ستون برای هر یک از دو ملکه برابر است. بنابراین
queens(i) + iبرای دو شاخص مختلفiمقدار یکسانی دارد. - اگر مورب صعودی باشد، تعداد ردیف منهای تعداد ستون برای هر یک از دو ملکه برابر است. در این مورد،
queens(i) - iبرای دو شاخص مختلفiدارای مقدار یکسانی است.
بنابراین محدودیت مورب این است که مقادیر queens(i) + i همه باید متفاوت باشند، و به همین ترتیب مقادیر queens(i) - i باید همه متفاوت باشند، برای i متفاوت.
کد بالا این محدودیت را با اعمال روش AllDifferent به queens[j] + j و queens[j] - j برای هر i اضافه می کند.
تصمیم ساز را اضافه کنید
مرحله بعدی ایجاد یک تصمیم ساز است که استراتژی جستجو را برای مشکل تعیین می کند. استراتژی جستجو میتواند تأثیر عمدهای بر زمان جستجو داشته باشد، به دلیل انتشار محدودیتها، که تعداد مقادیر متغیری را که حلکننده باید جستجو کند، کاهش میدهد. شما قبلاً نمونه ای از این را در مثال 4-queens دیده اید.
کد زیر یک تصمیم ساز با استفاده از روش حل کننده Phase ایجاد می کند.
پایتون
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase(
queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);جاوا
// Create the decision builder to search for solutions.
final DecisionBuilder db =
solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);سی شارپ
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
برای جزئیات بیشتر در مورد آرگومان های ورودی متد Phase به Decision builder مراجعه کنید.
نحوه عملکرد سازنده تصمیم در مثال 4-queens
بیایید نگاهی بیندازیم که سازنده تصمیم چگونه جستجو را در مثال 4-queens هدایت می کند. حل کننده با queens[0] ، اولین متغیر در آرایه، طبق دستور CHOOSE_FIRST_UNBOUND شروع می شود. سپس حلکننده کوچکترین مقداری را که قبلاً امتحان نشده است، به queens[0] اختصاص میدهد که در این مرحله طبق دستور ASSIGN_MIN_VALUE 0 است. این اولین ملکه را در گوشه سمت چپ بالای تخته قرار می دهد.
سپس، حلکننده queens[1] را انتخاب میکند، که اکنون اولین متغیر غیر محدود در queens است. پس از انتشار محدودیت ها، دو ردیف ممکن برای یک ملکه در ستون 1 وجود دارد: ردیف 2 یا ردیف 3. گزینه ASSIGN_MIN_VALUE به حل کننده هدایت می کند تا queens[1] = 2 . (اگر در عوض، IntValueStrategy روی ASSIGN_MAX_VALUE تنظیم کنید، حل کننده queens[1] = 3 )
می توانید بررسی کنید که بقیه جستجوها از همان قوانین پیروی می کند.
با حل کننده تماس بگیرید و نتایج را نمایش دهید
کد زیر حل کننده را اجرا می کند و راه حل را نمایش می دهد.
پایتون
# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
# Displays the solution just computed.
for i in range(board_size):
for j in range(board_size):
if queens[j].Value() == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
num_solutions += 1
solver.EndSearch()C++
// Iterates through the solutions, displaying each.
int num_solutions = 0;
solver.NewSearch(db);
while (solver.NextSolution()) {
// Displays the solution just computed.
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (queens[j]->Value() == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}
solver.EndSearch();جاوا
int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < boardSize; ++i) {
for (int j = 0; j < boardSize; ++j) {
if (queens[j].value() == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != boardSize - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
solver.endSearch();سی شارپ
// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
Console.WriteLine("Solution " + SolutionCount);
for (int i = 0; i < BoardSize; ++i)
{
for (int j = 0; j < BoardSize; ++j)
{
if (queens[j].Value() == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != BoardSize - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount++;
}
solver.EndSearch();در اینجا اولین راه حل یافت شده توسط برنامه برای یک برد 8x8 است.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92 میتوانید با ارسال N بهعنوان آرگومان خط فرمان، مشکل تختهای با اندازه متفاوت را حل کنید. به عنوان مثال، python nqueens_cp.py 6 مشکل یک برد 6x6 را حل می کند.
کل برنامه
برنامه کامل در زیر نشان داده شده است.
پایتون
"""OR-Tools solution to the N-queens problem."""
import sys
from ortools.constraint_solver import pywrapcp
def main(board_size):
# Creates the solver.
solver = pywrapcp.Solver("n-queens")
# Creates the variables.
# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
# Creates the constraints.
# All rows must be different.
solver.Add(solver.AllDifferent(queens))
# No two queens can be on the same diagonal.
solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
# Displays the solution just computed.
for i in range(board_size):
for j in range(board_size):
if queens[j].Value() == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
num_solutions += 1
solver.EndSearch()
# Statistics.
print("\nStatistics")
print(f" failures: {solver.Failures()}")
print(f" branches: {solver.Branches()}")
print(f" wall time: {solver.WallTime()} ms")
print(f" Solutions found: {num_solutions}")
if __name__ == "__main__":
# By default, solve the 8x8 problem.
size = 8
if len(sys.argv) > 1:
size = int(sys.argv[1])
main(size)C++
// OR-Tools solution to the N-queens problem.
#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>
#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"
namespace operations_research {
void NQueensCp(const int board_size) {
// Instantiate the solver.
Solver solver("N-Queens");
std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}
// Define constraints.
// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));
// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));
DecisionBuilder* const db = solver.MakePhase(
queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
// Iterates through the solutions, displaying each.
int num_solutions = 0;
solver.NewSearch(db);
while (solver.NextSolution()) {
// Displays the solution just computed.
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (queens[j]->Value() == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}
solver.EndSearch();
// Statistics.
LOG(INFO) << "Statistics";
LOG(INFO) << " failures: " << solver.failures();
LOG(INFO) << " branches: " << solver.branches();
LOG(INFO) << " wall time: " << solver.wall_time() << " ms";
LOG(INFO) << " Solutions found: " << num_solutions;
}
} // namespace operations_research
int main(int argc, char** argv) {
int board_size = 8;
if (argc > 1) {
board_size = std::atoi(argv[1]);
}
operations_research::NQueensCp(board_size);
return EXIT_SUCCESS;
}جاوا
// OR-Tools solution to the N-queens problem.
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;
/** N-Queens Problem. */
public final class NQueensCp {
public static void main(String[] args) {
Loader.loadNativeLibraries();
// Instantiate the solver.
Solver solver = new Solver("N-Queens");
int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}
// Define constraints.
// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = solver.makeSum(queens[i], i).var();
diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));
// Create the decision builder to search for solutions.
final DecisionBuilder db =
solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < boardSize; ++i) {
for (int j = 0; j < boardSize; ++j) {
if (queens[j].value() == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != boardSize - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
solver.endSearch();
// Statistics.
System.out.println("Statistics");
System.out.println(" failures: " + solver.failures());
System.out.println(" branches: " + solver.branches());
System.out.println(" wall time: " + solver.wallTime() + "ms");
System.out.println(" Solutions found: " + solutionCount);
}
private NQueensCp() {}
}سی شارپ
// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.ConstraintSolver;
public class NQueensCp
{
public static void Main(String[] args)
{
// Instantiate the solver.
Solver solver = new Solver("N-Queens");
const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
}
// Define constraints.
// All rows must be different.
solver.Add(queens.AllDifferent());
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = solver.MakeSum(queens[i], i).Var();
diag2[i] = solver.MakeSum(queens[i], -i).Var();
}
solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());
// Create the decision builder to search for solutions.
DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
Console.WriteLine("Solution " + SolutionCount);
for (int i = 0; i < BoardSize; ++i)
{
for (int j = 0; j < BoardSize; ++j)
{
if (queens[j].Value() == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != BoardSize - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount++;
}
solver.EndSearch();
// Statistics.
Console.WriteLine("Statistics");
Console.WriteLine($" failures: {solver.Failures()}");
Console.WriteLine($" branches: {solver.Branches()}");
Console.WriteLine($" wall time: {solver.WallTime()} ms");
Console.WriteLine($" Solutions found: {SolutionCount}");
}
}تعداد راه حل ها
تعداد راه حل ها تقریباً به صورت تصاعدی با اندازه تخته افزایش می یابد:
| اندازه تخته | راه حل ها | زمان یافتن همه راه حل ها (ms) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
بسیاری از راه حل ها فقط چرخش های دیگر هستند و تکنیکی به نام شکست تقارن می تواند برای کاهش میزان محاسبات مورد نیاز استفاده شود. ما در اینجا از آن استفاده نمی کنیم. راه حل ما در بالا سریع نیست، بلکه ساده است. البته، اگر بخواهیم به جای همه آنها فقط یک راه حل پیدا کنیم، می توانیم آن را بسیار سریعتر کنیم: برای اندازه تخته تا 50 بیشتر از چند میلی ثانیه.

