द एन-क्वींस प्रॉब्लम

नीचे दिए गए सेक्शन में, हम कंस्ट्रेंट प्रोग्रामिंग (सीपी) को शतरंज के खेल पर आधारित संयुक्त समस्या. शतरंज के खेल में रानी अटैक कर सकती है हॉरिज़ॉन्टल, वर्टिकल, और तिरछा. द एन-क्वींस सवाल पूछता है:

N क्वींस को NxN के शतरंज की बोर्ड पर कैसे रखा जा सकता है, ताकि दोनों हमला न करें एक-दूसरे को?

नीचे, N = 4 के लिए N-क्वींस की समस्या का एक संभावित हल देखा जा सकता है.

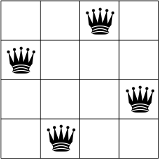
दो रानी एक ही पंक्ति, कॉलम या डायगनल में नहीं होती हैं.

ध्यान दें कि यह ऑप्टिमाइज़ेशन की समस्या नहीं है: हम उन सभी चीज़ों के बारे में जानना चाहते हैं एक इष्टतम समाधान के बजाय समाधान प्रदान करते हैं, जिससे यह एक स्वाभाविक उम्मीदवार बन जाता है कंस्ट्रेंट प्रोग्रामिंग के लिए. इन सेक्शन में एन-क्वींस की समस्या को हल करने के लिए सीपी के तरीके के बारे में बताया गया है और ऐसे प्रोग्राम पेश करते हैं जो CP-SAT सॉल्वर और ओरिजनल CP, दोनों का इस्तेमाल करके सवालों को हल करते हैं सॉल्वर.

एन-क्वींस की समस्या पर सीपी की रणनीति

सीपी सॉल्वर में, व्यवस्थित तरीके से सभी किसी सवाल के वैरिएबल के लिए वैल्यू असाइन करना. समस्या को हल कर सकें. 4-क्वींस की समस्या में, हल सबसे बाईं ओर से शुरू होता है और उसके बाद, हर कॉलम में एक रानी को क्रम से लगाता है. जो पहले किसी रानी ने हमला नहीं किया था.

प्रसार और बैकट्रैकिंग

कंस्ट्रेंट प्रोग्रामिंग सर्च के लिए दो मुख्य एलिमेंट हैं:

• प्रोपेगेशन — हर बार जब सॉल्वर किसी वैरिएबल को कोई वैल्यू असाइन करता है, असाइन नहीं किए गए कंस्ट्रेंट की संभावित वैल्यू पर पाबंदियां लगाती हैं वैरिएबल. ये पाबंदियां, आने वाले वैरिएबल असाइनमेंट में लागू होती हैं. उदाहरण के लिए, 4-क्वींस वाले सवाल में, हर बार जब सॉल्वर किसी रानी को जगह पर रखता है, तो पंक्ति में किसी अन्य रानी को नहीं रखा जा सकता और वर्तमान रानी के डायगनल को डायगनल से ऊपर नहीं रखा जा सकता. प्रचार करने की सुविधा वैरिएबल वैल्यू को सॉल्वर को एक्सप्लोर करना चाहिए.
• बैकट्रैकिंग तब होती है, जब सॉल्वर अगले जब तक सीमाओं की वजह से वैरिएबल सेट नहीं होता या फिर यह कोई समाधान ढूंढ लेता है. दोनों ही मामलों में, सॉल्वर पिछले चरण पर वापस जाता है और वैरिएबल की वैल्यू को बदलकर उस चरण को उस मान पर सेट कर दें जिसे पहले कभी आज़माया नहीं गया है. 4-क्वींस वाले उदाहरण में, इसका मतलब है, रानी को मौजूदा कॉलम के एक नए स्क्वेयर पर ले जाना.

इसके बाद, आपको दिखेगा कि कंस्ट्रेंट प्रोग्रामिंग, 4-क्वींस की समस्या हल करो.

मान लीजिए कि सॉल्वर के ऊपर बाईं ओर एक रानी को रखने से शुरुआत होती है कोना. यह एक तरह की परिकल्पना है; शायद इससे पता चल जाएगा कि कोई हल मौजूद नहीं है जिसके ऊपरी बाएं कोने में रानी है.

इस परिकल्पना को देखते हुए, हम किन सीमाओं का प्रचार कर सकते हैं? एक कंस्ट्रेंट यह है कि एक कॉलम में सिर्फ़ एक क्वीन हो सकती है (नीचे स्लेटी Xs के निशान वाली हैं) और दूसरी कंस्ट्रेंट एक ही डायगनल पर दो रानी को प्रतिबंधित करता है (नीचे लाल X).

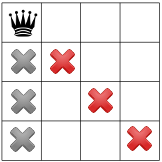
हमारी तीसरी सीमा, एक ही पंक्ति में रानी को प्रतिबंधित करती है:

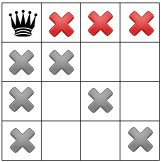
हमारी शर्तें लागू हुईं, तो हम दूसरे अनुमान की जांच कर सकते हैं और किसी बचे हुए स्क्वेयर में से एक में दूसरी क्वीन. हमारा सॉल्वर यह तय कर सकता है कि उसमें दूसरे कॉलम में पहले उपलब्ध वर्ग को डालने के लिए:

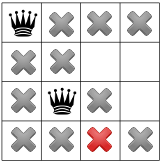
डायगनल कंस्ट्रेंट के आगे बढ़ने के बाद, हमने देखा कि इससे कोई तीसरे कॉलम या आखिरी पंक्ति में उपलब्ध वर्ग:

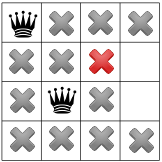
इस स्तर पर कोई समाधान संभव नहीं है और हमें ट्रैक करना होगा. एक विकल्प यह है ताकि सॉल्वर दूसरे कॉलम में मौजूद दूसरा स्क्वेयर चुन सके. हालांकि, कंस्ट्रेंट प्रोपगेशन के बाद, रानी को तीसरा कॉलम, चौथी रानी के लिए कोई मान्य जगह नहीं छोड़ी गई:

इसलिए, सॉल्वर को फिर से वापस जाना होगा. इस बार वह पहली रानी को रखना. हमने दिखाया है कि महारानी को कोई समाधान नहीं मिला सवाल किसी कोने के वर्ग का हिस्सा हो जाएगा.

किसी कोने में कोई क्वीन नहीं हो सकती, क्योंकि सॉल्वर पहले क्वीन को नीचे छोड़ देता है एक-एक करके आगे बढ़ता है और दूसरी रानी के लिए सिर्फ़ एक जगह छोड़ता है:

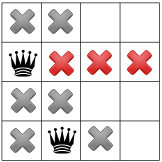
जब फिर से पता चलता है कि तीसरी रानी के लिए सिर्फ़ एक जगह बची है:

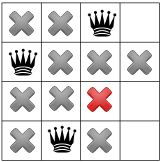
और चौथी और आखिरी रानी के लिए:

हमारे पास अपना पहला समाधान है! अगर हमने अपने सॉल्वर को तो यह यहां खत्म होगा. ऐसा न करने पर, वह फिर से हट जाएगा और पहली क्वीन को पहले कॉलम की तीसरी पंक्ति में रखें.

CP-SAT का इस्तेमाल करके समाधान

एन-क्वीन्स वाले सवाल, कंस्ट्रेंट प्रोग्रामिंग के हिसाब से सही है. इसमें सेक्शन में हम एक छोटे से Python प्रोग्राम के बारे में बताएंगे. इसमें CP-SAT सॉल्वर का इस्तेमाल इन कामों के लिए किया जाता है समस्या के सभी समाधान ढूंढें.

लाइब्रेरी इंपोर्ट करें

यहां दिया गया कोड ज़रूरी लाइब्रेरी इंपोर्ट करता है.

Python

import sys
import time
from ortools.sat.python import cp_model

C++

#include <stdlib.h>

#include <sstream>
#include <string>
#include <vector>

#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;

C#

using System;
using Google.OrTools.Sat;

मॉडल का एलान करना

यहां दिया गया कोड, CP-SAT मॉडल के बारे में बताता है.

Python

model = cp_model.CpModel()

C++

CpModelBuilder cp_model;

Java

CpModel model = new CpModel();

C#

        CpModel model = new CpModel();

        int BoardSize = 8;
        // There are `BoardSize` number of variables, one for a queen in each
        // column of the board. The value of each variable is the row that the
        // queen is in.
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        model.AddAllDifferent(queens);

        // No two queens can be on the same diagonal.
        LinearExpr[] diag1 = new LinearExpr[BoardSize];
        LinearExpr[] diag2 = new LinearExpr[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
            diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
        }

        model.AddAllDifferent(diag1);
        model.AddAllDifferent(diag2);

        // Creates a solver and solves the model.
        CpSolver solver = new CpSolver();
        SolutionPrinter cb = new SolutionPrinter(queens);
        // Search for all solutions.
        solver.StringParameters = "enumerate_all_solutions:true";
        // And solve.
        solver.Solve(model, cb);

        Console.WriteLine("Statistics");
        Console.WriteLine($"  conflicts : {solver.NumConflicts()}");
        Console.WriteLine($"  branches  : {solver.NumBranches()}");
        Console.WriteLine($"  wall time : {solver.WallTime()} s");
        Console.WriteLine($"  number of solutions found: {cb.SolutionCount()}");
    }
}

वैरिएबल बनाना

सॉल्वर, सवाल के लिए वैरिएबल को queens नाम वाले कलेक्शन के तौर पर बनाता है.

Python

# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]

C++

// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
  queens.push_back(
      cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}

Java

int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}

C#

int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}

यहां हम मानते हैं कि queens[j], कॉलम j में क्वीन के लिए पंक्ति की संख्या है. दूसरे शब्दों में, queens[j] = i का मतलब है कि लाइन i और कॉलम j में क्वीन है.

ध्यान दें: किसी हल का डायग्राम बनाते समय, आपको एक अलग तस्वीर मिलेगी पंक्तियों को नीचे से ऊपर की ओर या ऊपर से नीचे की ओर क्रम में लगाया गया है ( साथ ही, कॉलम बाईं से दाईं ओर या इसके उलट भी. हालांकि, क्रम बदलने से, सभी संभावित समाधानों के सेट में कोई बदलाव नहीं होता, बल्कि को डायग्राम में दिखाया गया है.

कंस्ट्रेंट बनाएं

यह कोड समस्या के लिए सीमाएं बनाता है.

Python

# All rows must be different.
model.add_all_different(queens)

# No two queens can be on the same diagonal.
model.add_all_different(queens[i] + i for i in range(board_size))
model.add_all_different(queens[i] - i for i in range(board_size))

C++

// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);

// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  diag_1.push_back(queens[i] + i);
  diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);

Java

// All rows must be different.
model.addAllDifferent(queens);

// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
  diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
  diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);

C#

// All rows must be different.
model.AddAllDifferent(queens);

// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
    diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}

model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);

यह कोड AddAllDifferent तरीके का इस्तेमाल करता है, जिसके लिए सभी एलिमेंट की ज़रूरत होती है वैरिएबल अरे को अलग करें.

चलिए देखते हैं कि इन कंस्ट्रेंट से, एन-क्वींस के लिए तीन स्थितियों की गारंटी कैसे मिलती है समस्या (अलग-अलग पंक्तियों, कॉलम, और डायगनल पर क्वींस).

एक ही पंक्ति में कोई दो क्वींस नहीं हैं

सॉल्वर के AllDifferent तरीके को queens पर लागू करने से, queens[j], हर j के लिए अलग-अलग होगा. इसका मतलब है कि सभी रानी को इसमें होना चाहिए अलग-अलग लाइन में रखें.

एक ही कॉलम पर दो क्वींस नहीं हैं

यह कंस्ट्रेंट, queens की परिभाषा में लागू है. queens के किसी भी दो एलिमेंट का इंडेक्स एक जैसा नहीं हो सकता. इसलिए, कोई भी दो क्वीन नहीं हो सकतीं डालें.

एक ही डायगनल पर दो रानी नहीं होती

डायगनल कंस्ट्रेंट, पंक्ति और कॉलम कंस्ट्रेंट की तुलना में थोड़ा पेचीदा होता है. पहला, अगर दो रानियां एक ही विकर्ण में लेटी हैं, तो नीचे दी गई स्थितियों में से एक सही होना चाहिए:

• दोनों रानी के लिए पंक्ति और कॉलम की संख्या बराबर होती है. दूसरे शब्दों में, दो अलग-अलग इंडेक्स के लिए queens(j) + j की वैल्यू एक जैसी है j.
• दोनों रानी में से हर एक के लिए, पंक्ति की संख्या में से कॉलम की संख्या को घटाने पर मिलने वाली संख्या बराबर होती है. इस मामले में, दो अलग-अलग इंडेक्स j के लिए queens(j) - j की वैल्यू एक जैसी है.

इनमें से एक स्थिति का मतलब है कि रानियां एक ही बढ़ते क्रम में डायगनल ( बाईं से दाईं ओर जा रहे हैं, जबकि दूसरे का मतलब है कि वे एक ही क्रम में घटते क्रम में हैं डायगनल. कौनसी शर्त बढ़ते क्रम में है और कौनसी घटती है पंक्तियों और कॉलम के क्रम पर निर्भर करता है. जैसा कि इसमें बताया गया है पिछला सेक्शन, ऑर्डर करने की प्रोसेस का कोई असर और उन्हें विज़ुअलाइज़ करने के तरीके के आधार पर उन्हें हल करें.

इसलिए डायगनल कंस्ट्रेंट का मतलब है कि queens(j) + j की सभी वैल्यू और queens(j) - j की सभी वैल्यू अलग-अलग होनी चाहिए भिन्न j.

queens(j) + j पर AddAllDifferent तरीका लागू करने के लिए, हम N इंस्टेंस डालते हैं वैरिएबल को j के लिए 0 से N-1 तक, diag1 की कलेक्शन में, इस तरह से दिखाया गया है:

q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i)
diag1.append(q1)
model.Add(q1 == queens[j] + j)

इसके बाद, हम diag1 पर AddAllDifferent लागू करते हैं.

model.AddAllDifferent(diag1)

queens(j) - j के लिए कंस्ट्रेंट इसी तरह बनाया गया है.

सलूशन प्रिंटर बनाएं

N-क्वींस समस्या के सभी समाधान प्रिंट करने के लिए, आपको एक कॉलबैक पास करना होगा, सॉलूशन प्रिंटर भी कहा जाता है. कॉलबैक हर एक को प्रिंट करता है मिल जाता है. यह कोड एक समाधान बनाता है प्रिंटर.

Python

class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
    """Print intermediate solutions."""

    def __init__(self, queens: list[cp_model.IntVar]):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__queens = queens
        self.__solution_count = 0
        self.__start_time = time.time()

    @property
    def solution_count(self) -> int:
        return self.__solution_count

    def on_solution_callback(self):
        current_time = time.time()
        print(
            f"Solution {self.__solution_count}, "
            f"time = {current_time - self.__start_time} s"
        )
        self.__solution_count += 1

        all_queens = range(len(self.__queens))
        for i in all_queens:
            for j in all_queens:
                if self.value(self.__queens[j]) == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()

C++

int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
  LOG(INFO) << "Solution " << num_solutions;
  for (int i = 0; i < board_size; ++i) {
    std::stringstream ss;
    for (int j = 0; j < board_size; ++j) {
      if (SolutionIntegerValue(response, queens[j]) == i) {
        // There is a queen in column j, row i.
        ss << "Q";
      } else {
        ss << "_";
      }
      if (j != board_size - 1) ss << " ";
    }
    LOG(INFO) << ss.str();
  }
  num_solutions++;
}));

Java

static class SolutionPrinter extends CpSolverSolutionCallback {
  public SolutionPrinter(IntVar[] queensIn) {
    solutionCount = 0;
    queens = queensIn;
  }

  @Override
  public void onSolutionCallback() {
    System.out.println("Solution " + solutionCount);
    for (int i = 0; i < queens.length; ++i) {
      for (int j = 0; j < queens.length; ++j) {
        if (value(queens[j]) == i) {
          System.out.print("Q");
        } else {
          System.out.print("_");
        }
        if (j != queens.length - 1) {
          System.out.print(" ");
        }
      }
      System.out.println();
    }
    solutionCount++;
  }

  public int getSolutionCount() {
    return solutionCount;
  }

  private int solutionCount;
  private final IntVar[] queens;
}

C#

public class SolutionPrinter : CpSolverSolutionCallback
{
    public SolutionPrinter(IntVar[] queens)
    {
        queens_ = queens;
    }

    public override void OnSolutionCallback()
    {
        Console.WriteLine($"Solution {SolutionCount_}");
        for (int i = 0; i < queens_.Length; ++i)
        {
            for (int j = 0; j < queens_.Length; ++j)
            {
                if (Value(queens_[j]) == i)
                {
                    Console.Write("Q");
                }
                else
                {
                    Console.Write("_");
                }
                if (j != queens_.Length - 1)
                    Console.Write(" ");
            }
            Console.WriteLine("");
        }
        SolutionCount_++;
    }

    public int SolutionCount()
    {
        return SolutionCount_;
    }

    private int SolutionCount_;
    private IntVar[] queens_;
}

ध्यान दें कि सलूशन प्रिंटर को Python क्लास के तौर पर लिखा जाना चाहिए, क्योंकि C++ सॉल्वर में Python इंटरफ़ेस.

सलूशन प्रिंटर में, नीचे दी गई लाइनों की मदद से समाधान प्रिंट किए जाते हैं.

for v in self.__variables:
print('%s = %i' % (v, self.Value(v)), end = ' ')

इस उदाहरण में, self.__variables वैरिएबल queens है और हर v queens की आठ एंट्री में से किसी एक के मुताबिक है. यह निम्न फ़ॉर्म: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) जहां xi, i पंक्ति में क्वीन का कॉलम नंबर है.

अगले सेक्शन में, समाधान का एक उदाहरण दिया गया है.

सॉल्वर को कॉल करें और नतीजे देखें

यहां दिया गया कोड, सॉल्वर को चलाता है और उसे हल करता है.

Python

solver = cp_model.CpSolver()
solution_printer = NQueenSolutionPrinter(queens)
solver.parameters.enumerate_all_solutions = True
solver.solve(model, solution_printer)

C++

// Tell the solver to enumerate all solutions.
SatParameters parameters;
parameters.set_enumerate_all_solutions(true);
model.Add(NewSatParameters(parameters));

const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
LOG(INFO) << "Number of solutions found: " << num_solutions;

Java

CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Tell the solver to enumerate all solutions.
solver.getParameters().setEnumerateAllSolutions(true);
// And solve.
solver.solve(model, cb);

C#

// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);

इस प्रोग्राम के तहत, 8x8 बोर्ड के लिए 92 अलग-अलग समाधान ढूंढे जाते हैं. यह रहा पहला सवाल।

        Q _ _ _ _ _ _ _
        _ _ _ _ _ _ Q _
        _ _ _ _ Q _ _ _
        _ _ _ _ _ _ _ Q
        _ Q _ _ _ _ _ _
        _ _ _ Q _ _ _ _
        _ _ _ _ _ Q _ _
        _ _ Q _ _ _ _ _
        ...91 other solutions displayed...
        Solutions found: 92

आप किसी दूसरे आकार के बोर्ड के लिए सवाल को हल करने के लिए, कमांड लाइन आर्ग्युमेंट. उदाहरण के लिए, अगर प्रोग्राम का नाम queens है, python nqueens_sat.py 6 6x6 बोर्ड के लिए सवाल हल करता है.

पूरा प्रोग्राम

एन-क्वींस प्रोग्राम का पूरा प्रोग्राम यहां दिया गया है.

Python

"""OR-Tools solution to the N-queens problem."""
import sys
import time
from ortools.sat.python import cp_model


class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
    """Print intermediate solutions."""

    def __init__(self, queens: list[cp_model.IntVar]):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__queens = queens
        self.__solution_count = 0
        self.__start_time = time.time()

    @property
    def solution_count(self) -> int:
        return self.__solution_count

    def on_solution_callback(self):
        current_time = time.time()
        print(
            f"Solution {self.__solution_count}, "
            f"time = {current_time - self.__start_time} s"
        )
        self.__solution_count += 1

        all_queens = range(len(self.__queens))
        for i in all_queens:
            for j in all_queens:
                if self.value(self.__queens[j]) == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()



def main(board_size: int) -> None:
    # Creates the solver.
    model = cp_model.CpModel()

    # Creates the variables.
    # There are `board_size` number of variables, one for a queen in each column
    # of the board. The value of each variable is the row that the queen is in.
    queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]

    # Creates the constraints.
    # All rows must be different.
    model.add_all_different(queens)

    # No two queens can be on the same diagonal.
    model.add_all_different(queens[i] + i for i in range(board_size))
    model.add_all_different(queens[i] - i for i in range(board_size))

    # Solve the model.
    solver = cp_model.CpSolver()
    solution_printer = NQueenSolutionPrinter(queens)
    solver.parameters.enumerate_all_solutions = True
    solver.solve(model, solution_printer)

    # Statistics.
    print("\nStatistics")
    print(f"  conflicts      : {solver.num_conflicts}")
    print(f"  branches       : {solver.num_branches}")
    print(f"  wall time      : {solver.wall_time} s")
    print(f"  solutions found: {solution_printer.solution_count}")


if __name__ == "__main__":
    # By default, solve the 8x8 problem.
    size = 8
    if len(sys.argv) > 1:
        size = int(sys.argv[1])
    main(size)

C++

// OR-Tools solution to the N-queens problem.
#include <stdlib.h>

#include <sstream>
#include <string>
#include <vector>

#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"

namespace operations_research {
namespace sat {

void NQueensSat(const int board_size) {
  // Instantiate the solver.
  CpModelBuilder cp_model;

  // There are `board_size` number of variables, one for a queen in each column
  // of the board. The value of each variable is the row that the queen is in.
  std::vector<IntVar> queens;
  queens.reserve(board_size);
  Domain range(0, board_size - 1);
  for (int i = 0; i < board_size; ++i) {
    queens.push_back(
        cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
  }

  // Define constraints.
  // The following sets the constraint that all queens are in different rows.
  cp_model.AddAllDifferent(queens);

  // No two queens can be on the same diagonal.
  std::vector<LinearExpr> diag_1;
  diag_1.reserve(board_size);
  std::vector<LinearExpr> diag_2;
  diag_2.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    diag_1.push_back(queens[i] + i);
    diag_2.push_back(queens[i] - i);
  }
  cp_model.AddAllDifferent(diag_1);
  cp_model.AddAllDifferent(diag_2);

  int num_solutions = 0;
  Model model;
  model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
    LOG(INFO) << "Solution " << num_solutions;
    for (int i = 0; i < board_size; ++i) {
      std::stringstream ss;
      for (int j = 0; j < board_size; ++j) {
        if (SolutionIntegerValue(response, queens[j]) == i) {
          // There is a queen in column j, row i.
          ss << "Q";
        } else {
          ss << "_";
        }
        if (j != board_size - 1) ss << " ";
      }
      LOG(INFO) << ss.str();
    }
    num_solutions++;
  }));

  // Tell the solver to enumerate all solutions.
  SatParameters parameters;
  parameters.set_enumerate_all_solutions(true);
  model.Add(NewSatParameters(parameters));

  const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
  LOG(INFO) << "Number of solutions found: " << num_solutions;

  // Statistics.
  LOG(INFO) << "Statistics";
  LOG(INFO) << CpSolverResponseStats(response);
}

}  // namespace sat
}  // namespace operations_research

int main(int argc, char** argv) {
  int board_size = 8;
  if (argc > 1) {
    if (!absl::SimpleAtoi(argv[1], &board_size)) {
      LOG(INFO) << "Cannot parse '" << argv[1]
                << "', using the default value of 8.";
      board_size = 8;
    }
  }
  operations_research::sat::NQueensSat(board_size);
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.sat.samples;
import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;

/** OR-Tools solution to the N-queens problem. */
public final class NQueensSat {
  static class SolutionPrinter extends CpSolverSolutionCallback {
    public SolutionPrinter(IntVar[] queensIn) {
      solutionCount = 0;
      queens = queensIn;
    }

    @Override
    public void onSolutionCallback() {
      System.out.println("Solution " + solutionCount);
      for (int i = 0; i < queens.length; ++i) {
        for (int j = 0; j < queens.length; ++j) {
          if (value(queens[j]) == i) {
            System.out.print("Q");
          } else {
            System.out.print("_");
          }
          if (j != queens.length - 1) {
            System.out.print(" ");
          }
        }
        System.out.println();
      }
      solutionCount++;
    }

    public int getSolutionCount() {
      return solutionCount;
    }

    private int solutionCount;
    private final IntVar[] queens;
  }

  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Create the model.
    CpModel model = new CpModel();

    int boardSize = 8;
    // There are `BoardSize` number of variables, one for a queen in each column of the board. The
    // value of each variable is the row that the queen is in.
    IntVar[] queens = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
    }

    // Define constraints.
    // All rows must be different.
    model.addAllDifferent(queens);

    // No two queens can be on the same diagonal.
    LinearExpr[] diag1 = new LinearExpr[boardSize];
    LinearExpr[] diag2 = new LinearExpr[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
      diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
    }
    model.addAllDifferent(diag1);
    model.addAllDifferent(diag2);

    // Create a solver and solve the model.
    CpSolver solver = new CpSolver();
    SolutionPrinter cb = new SolutionPrinter(queens);
    // Tell the solver to enumerate all solutions.
    solver.getParameters().setEnumerateAllSolutions(true);
    // And solve.
    solver.solve(model, cb);

    // Statistics.
    System.out.println("Statistics");
    System.out.println("  conflicts : " + solver.numConflicts());
    System.out.println("  branches  : " + solver.numBranches());
    System.out.println("  wall time : " + solver.wallTime() + " s");
    System.out.println("  solutions : " + cb.getSolutionCount());
  }

  private NQueensSat() {}
}

C#

// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.Sat;

public class NQueensSat
{
    public class SolutionPrinter : CpSolverSolutionCallback
    {
        public SolutionPrinter(IntVar[] queens)
        {
            queens_ = queens;
        }

        public override void OnSolutionCallback()
        {
            Console.WriteLine($"Solution {SolutionCount_}");
            for (int i = 0; i < queens_.Length; ++i)
            {
                for (int j = 0; j < queens_.Length; ++j)
                {
                    if (Value(queens_[j]) == i)
                    {
                        Console.Write("Q");
                    }
                    else
                    {
                        Console.Write("_");
                    }
                    if (j != queens_.Length - 1)
                        Console.Write(" ");
                }
                Console.WriteLine("");
            }
            SolutionCount_++;
        }

        public int SolutionCount()
        {
            return SolutionCount_;
        }

        private int SolutionCount_;
        private IntVar[] queens_;
    }

    static void Main()
    {
        // Constraint programming engine
        CpModel model = new CpModel();

        int BoardSize = 8;
        // There are `BoardSize` number of variables, one for a queen in each
        // column of the board. The value of each variable is the row that the
        // queen is in.
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        model.AddAllDifferent(queens);

        // No two queens can be on the same diagonal.
        LinearExpr[] diag1 = new LinearExpr[BoardSize];
        LinearExpr[] diag2 = new LinearExpr[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
            diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
        }

        model.AddAllDifferent(diag1);
        model.AddAllDifferent(diag2);

        // Creates a solver and solves the model.
        CpSolver solver = new CpSolver();
        SolutionPrinter cb = new SolutionPrinter(queens);
        // Search for all solutions.
        solver.StringParameters = "enumerate_all_solutions:true";
        // And solve.
        solver.Solve(model, cb);

        Console.WriteLine("Statistics");
        Console.WriteLine($"  conflicts : {solver.NumConflicts()}");
        Console.WriteLine($"  branches  : {solver.NumBranches()}");
        Console.WriteLine($"  wall time : {solver.WallTime()} s");
        Console.WriteLine($"  number of solutions found: {cb.SolutionCount()}");
    }
}

ओरिजनल सीपी सॉल्वर की मदद से समाधान

नीचे दिए गए सेक्शन में एक Python प्रोग्राम दिखाया गया है, जो ओरिजनल सीपी सॉल्वर की जानकारी देंगे. हालांकि, हमारा सुझाव है कि आप नया CP-SAT सॉल्वर इस्तेमाल करें)

लाइब्रेरी इंपोर्ट करें

यहां दिया गया कोड ज़रूरी लाइब्रेरी इंपोर्ट करता है.

Python

import sys
from ortools.constraint_solver import pywrapcp

C++

#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>

#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;

C#

using System;
using Google.OrTools.ConstraintSolver;

सॉल्वर के बारे में बताओ

यहां दिया गया कोड, ओरिजनल सीपी सॉल्वर के बारे में बताता है.

Python

solver = pywrapcp.Solver("n-queens")

C++

Solver solver("N-Queens");

Java

Solver solver = new Solver("N-Queens");

C#

Solver solver = new Solver("N-Queens");

वैरिएबल बनाना

सॉल्वर का IntVar तरीका, सवाल के अरे के तौर पर वैरिएबल बनाता है queens नाम दिया गया है.

Python

# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]

C++

std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  queens.push_back(
      solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}

Java

int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}

C#

const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
}

किसी भी हल के लिए, queens[j] = i का मतलब है कि कॉलम j और पंक्ति में एक क्वीन है i.

कंस्ट्रेंट बनाएं

यह कोड समस्या के लिए सीमाएं बनाता है.

Python

# All rows must be different.
solver.Add(solver.AllDifferent(queens))

# No two queens can be on the same diagonal.
solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))

C++

// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));

// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
  diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));

Java

// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));

// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  diag1[i] = solver.makeSum(queens[i], i).var();
  diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));

C#

// All rows must be different.
solver.Add(queens.AllDifferent());

// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    diag1[i] = solver.MakeSum(queens[i], i).Var();
    diag2[i] = solver.MakeSum(queens[i], -i).Var();
}

solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());

ये कंस्ट्रेंट, एन-क्वीन्स की समस्या ( क्वींस के लिए अलग-अलग लाइन, कॉलम, और डायगनल बनाए जा सकते हैं.

एक ही पंक्ति में कोई दो क्वींस नहीं हैं

सॉल्वर के AllDifferent तरीके को queens पर लागू करने से, queens[j], हर j के लिए अलग-अलग होगा. इसका मतलब है कि सभी रानी को इसमें होना चाहिए अलग-अलग लाइन में रखें.

एक ही कॉलम पर दो क्वींस नहीं हैं

यह कंस्ट्रेंट, queens की परिभाषा में लागू है. queens के किसी भी दो एलिमेंट का इंडेक्स एक जैसा नहीं हो सकता. इसलिए, कोई भी दो क्वीन नहीं हो सकतीं डालें.

एक ही डायगनल पर दो रानी नहीं होती

डायगनल कंस्ट्रेंट, पंक्ति और कॉलम कंस्ट्रेंट की तुलना में थोड़ा पेचीदा होता है. पहला, अगर दो रानी एक ही डायगनल पर लेटी हैं, तो इन चीज़ों में से कोई एक सही होनी चाहिए:

• अगर डायगनल घटते क्रम में (बाएं से दाएं की तरफ़ जा रहा है), तो पंक्ति की संख्या दोनों रानी के कॉलम की संख्या बराबर है. इसलिए, queens(i) + i के पास दो अलग-अलग इंडेक्स i के लिए एक ही मान है.
• अगर डायगनल आरोही है, तो पंक्ति की संख्या में से हर एक के लिए कॉलम की संख्या घटाएं दो रानियों में से एक बराबर है. इस मामले में, queens(i) - i की वैल्यू एक जैसी है दो अलग-अलग इंडेक्स के लिए, i.

इसलिए डायगनल कंस्ट्रेंट का मतलब है कि queens(i) + i की सभी वैल्यू और queens(i) - i की सभी वैल्यू अलग-अलग होनी चाहिए. भिन्न i.

ऊपर दिया गया कोड AllDifferent queens[j] + j और queens[j] - j के लिए, हर i का तरीका.

डिसिज़न बिल्डर जोड़ना

अगला चरण डिसिज़न बिल्डर बनाना है, जिससे सर्च स्ट्रेटजी सेट हो जाएगी समस्या हल करने के लिए. खोज की रणनीति, खोज के समय पर बड़ा असर डाल सकती है. पाबंदियों के लागू होने की वजह से होता है. इससे वैरिएबल वैल्यू की संख्या कम हो जाती है सॉल्वर को एक्सप्लोर करना होगा. आपने पहले ही यहां इसका उदाहरण देखा है: 4-क्वींस का उदाहरण.

यहां दिया गया कोड, सॉल्वर के तरीके का इस्तेमाल करके डिसिज़न बिल्डर बनाता है Phase तरीका.

Python

db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

C++

DecisionBuilder* const db = solver.MakePhase(
    queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);

Java

// Create the decision builder to search for solutions.
final DecisionBuilder db =
    solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

C#

// Create the decision builder to search for solutions.
DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

इस बारे में जानकारी के लिए, डिसिज़न बिल्डर देखें Phase तरीके में इनपुट के लिए तर्क डालें.

4-क्वींस के उदाहरण में डिसिज़न बिल्डर कैसे काम करता है

चलिए, देखते हैं कि डिसिज़न बिल्डर, खोज के नतीजों को 4-क्वींस का उदाहरण. सॉल्वर की शुरुआत queens[0] से होती है. यह निर्देशों के मुताबिक, अरे में पहला वैरिएबल होता है CHOOSE_FIRST_UNBOUND ने. इसके बाद, सॉल्वर, सबसे छोटी वैल्यू queens[0] को असाइन करता है वह मान जिसे पहले कभी आज़माया नहीं गया है, जो इस चरण में 0 है, जैसा कि इसके निर्देशित है ASSIGN_MIN_VALUE. यह स्थान के ऊपरी बाएं कोने में पहली रानी को जगह देता है बोर्ड.

इसके बाद, सॉल्वर queens[1] को चुनता है, जो अब इसमें पहला अनबाउंड वैरिएबल है queens. कंस्ट्रेंट लागू होने के बाद, दो लाइनें हो सकती हैं: कॉलम 1 में क्वीन: पंक्ति 2 या पंक्ति 3. ASSIGN_MIN_VALUE विकल्प, सॉल्वर का इस्तेमाल करके, queens[1] = 2 असाइन करें. (अगर इसके बजाय, आपने IntValueStrategy को ASSIGN_MAX_VALUE, सॉल्वर queens[1] = 3 असाइन करेगा.)

यह देखा जा सकता है कि अन्य सभी खोज के लिए, एक जैसे नियमों का पालन किया गया है या नहीं.

सॉल्वर को कॉल करें और नतीजे देखें

यहां दिया गया कोड, सॉल्वर को चलाता है और उसे हल करता है.

Python

# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
    # Displays the solution just computed.
    for i in range(board_size):
        for j in range(board_size):
            if queens[j].Value() == i:
                # There is a queen in column j, row i.
                print("Q", end=" ")
            else:
                print("_", end=" ")
        print()
    print()
    num_solutions += 1
solver.EndSearch()

C++

// Iterates through the solutions, displaying each.
int num_solutions = 0;

solver.NewSearch(db);
while (solver.NextSolution()) {
  // Displays the solution just computed.
  LOG(INFO) << "Solution " << num_solutions;
  for (int i = 0; i < board_size; ++i) {
    std::stringstream ss;
    for (int j = 0; j < board_size; ++j) {
      if (queens[j]->Value() == i) {
        // There is a queen in column j, row i.
        ss << "Q";
      } else {
        ss << "_";
      }
      if (j != board_size - 1) ss << " ";
    }
    LOG(INFO) << ss.str();
  }
  num_solutions++;
}
solver.EndSearch();

Java

int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
  System.out.println("Solution " + solutionCount);
  for (int i = 0; i < boardSize; ++i) {
    for (int j = 0; j < boardSize; ++j) {
      if (queens[j].value() == i) {
        System.out.print("Q");
      } else {
        System.out.print("_");
      }
      if (j != boardSize - 1) {
        System.out.print(" ");
      }
    }
    System.out.println();
  }
  solutionCount++;
}
solver.endSearch();

C#

// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
    Console.WriteLine("Solution " + SolutionCount);
    for (int i = 0; i < BoardSize; ++i)
    {
        for (int j = 0; j < BoardSize; ++j)
        {
            if (queens[j].Value() == i)
            {
                Console.Write("Q");
            }
            else
            {
                Console.Write("_");
            }
            if (j != BoardSize - 1)
                Console.Write(" ");
        }
        Console.WriteLine("");
    }
    SolutionCount++;
}
solver.EndSearch();

8x8 बोर्ड के लिए प्रोग्राम से मिला पहला समाधान यहां दिया गया है.

        Q _ _ _ _ _ _ _
        _ _ _ _ _ _ Q _
        _ _ _ _ Q _ _ _
        _ _ _ _ _ _ _ Q
        _ Q _ _ _ _ _ _
        _ _ _ Q _ _ _ _
        _ _ _ _ _ Q _ _
        _ _ Q _ _ _ _ _
        ...91 other solutions displayed...
        Statistics
        failures: 304
        branches: 790
        wall time: 5 ms
        Solutions found: 92

आप किसी दूसरे आकार के बोर्ड के लिए सवाल को हल करने के लिए, कमांड लाइन आर्ग्युमेंट. उदाहरण के लिए, python nqueens_cp.py 6 से सवाल हल हो जाता है 6x6 बोर्ड के लिए.

पूरा प्रोग्राम

पूरा प्रोग्राम नीचे दिखाया गया है.

Python

"""OR-Tools solution to the N-queens problem."""
import sys
from ortools.constraint_solver import pywrapcp


def main(board_size):
    # Creates the solver.
    solver = pywrapcp.Solver("n-queens")

    # Creates the variables.
    # The array index is the column, and the value is the row.
    queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]

    # Creates the constraints.
    # All rows must be different.
    solver.Add(solver.AllDifferent(queens))

    # No two queens can be on the same diagonal.
    solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
    solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))

    db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

    # Iterates through the solutions, displaying each.
    num_solutions = 0
    solver.NewSearch(db)
    while solver.NextSolution():
        # Displays the solution just computed.
        for i in range(board_size):
            for j in range(board_size):
                if queens[j].Value() == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()
        num_solutions += 1
    solver.EndSearch()

    # Statistics.
    print("\nStatistics")
    print(f"  failures: {solver.Failures()}")
    print(f"  branches: {solver.Branches()}")
    print(f"  wall time: {solver.WallTime()} ms")
    print(f"  Solutions found: {num_solutions}")


if __name__ == "__main__":
    # By default, solve the 8x8 problem.
    size = 8
    if len(sys.argv) > 1:
        size = int(sys.argv[1])
    main(size)

C++

// OR-Tools solution to the N-queens problem.
#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>

#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"

namespace operations_research {

void NQueensCp(const int board_size) {
  // Instantiate the solver.
  Solver solver("N-Queens");

  std::vector<IntVar*> queens;
  queens.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    queens.push_back(
        solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
  }

  // Define constraints.
  // The following sets the constraint that all queens are in different rows.
  solver.AddConstraint(solver.MakeAllDifferent(queens));

  // All columns must be different because the indices of queens are all
  // different. No two queens can be on the same diagonal.
  std::vector<IntVar*> diag_1;
  diag_1.reserve(board_size);
  std::vector<IntVar*> diag_2;
  diag_2.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
    diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
  }
  solver.AddConstraint(solver.MakeAllDifferent(diag_1));
  solver.AddConstraint(solver.MakeAllDifferent(diag_2));

  DecisionBuilder* const db = solver.MakePhase(
      queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);

  // Iterates through the solutions, displaying each.
  int num_solutions = 0;

  solver.NewSearch(db);
  while (solver.NextSolution()) {
    // Displays the solution just computed.
    LOG(INFO) << "Solution " << num_solutions;
    for (int i = 0; i < board_size; ++i) {
      std::stringstream ss;
      for (int j = 0; j < board_size; ++j) {
        if (queens[j]->Value() == i) {
          // There is a queen in column j, row i.
          ss << "Q";
        } else {
          ss << "_";
        }
        if (j != board_size - 1) ss << " ";
      }
      LOG(INFO) << ss.str();
    }
    num_solutions++;
  }
  solver.EndSearch();

  // Statistics.
  LOG(INFO) << "Statistics";
  LOG(INFO) << "  failures: " << solver.failures();
  LOG(INFO) << "  branches: " << solver.branches();
  LOG(INFO) << "  wall time: " << solver.wall_time() << " ms";
  LOG(INFO) << "  Solutions found: " << num_solutions;
}

}  // namespace operations_research

int main(int argc, char** argv) {
  int board_size = 8;
  if (argc > 1) {
    board_size = std::atoi(argv[1]);
  }
  operations_research::NQueensCp(board_size);
  return EXIT_SUCCESS;
}

Java

// OR-Tools solution to the N-queens problem.
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;

/** N-Queens Problem. */
public final class NQueensCp {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Instantiate the solver.
    Solver solver = new Solver("N-Queens");

    int boardSize = 8;
    IntVar[] queens = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
    }

    // Define constraints.
    // All rows must be different.
    solver.addConstraint(solver.makeAllDifferent(queens));

    // All columns must be different because the indices of queens are all different.
    // No two queens can be on the same diagonal.
    IntVar[] diag1 = new IntVar[boardSize];
    IntVar[] diag2 = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      diag1[i] = solver.makeSum(queens[i], i).var();
      diag2[i] = solver.makeSum(queens[i], -i).var();
    }
    solver.addConstraint(solver.makeAllDifferent(diag1));
    solver.addConstraint(solver.makeAllDifferent(diag2));

    // Create the decision builder to search for solutions.
    final DecisionBuilder db =
        solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

    int solutionCount = 0;
    solver.newSearch(db);
    while (solver.nextSolution()) {
      System.out.println("Solution " + solutionCount);
      for (int i = 0; i < boardSize; ++i) {
        for (int j = 0; j < boardSize; ++j) {
          if (queens[j].value() == i) {
            System.out.print("Q");
          } else {
            System.out.print("_");
          }
          if (j != boardSize - 1) {
            System.out.print(" ");
          }
        }
        System.out.println();
      }
      solutionCount++;
    }
    solver.endSearch();

    // Statistics.
    System.out.println("Statistics");
    System.out.println("  failures: " + solver.failures());
    System.out.println("  branches: " + solver.branches());
    System.out.println("  wall time: " + solver.wallTime() + "ms");
    System.out.println("  Solutions found: " + solutionCount);
  }

  private NQueensCp() {}
}

C#

// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.ConstraintSolver;

public class NQueensCp
{
    public static void Main(String[] args)
    {
        // Instantiate the solver.
        Solver solver = new Solver("N-Queens");

        const int BoardSize = 8;
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        solver.Add(queens.AllDifferent());

        // All columns must be different because the indices of queens are all different.
        // No two queens can be on the same diagonal.
        IntVar[] diag1 = new IntVar[BoardSize];
        IntVar[] diag2 = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = solver.MakeSum(queens[i], i).Var();
            diag2[i] = solver.MakeSum(queens[i], -i).Var();
        }

        solver.Add(diag1.AllDifferent());
        solver.Add(diag2.AllDifferent());

        // Create the decision builder to search for solutions.
        DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

        // Iterates through the solutions, displaying each.
        int SolutionCount = 0;
        solver.NewSearch(db);
        while (solver.NextSolution())
        {
            Console.WriteLine("Solution " + SolutionCount);
            for (int i = 0; i < BoardSize; ++i)
            {
                for (int j = 0; j < BoardSize; ++j)
                {
                    if (queens[j].Value() == i)
                    {
                        Console.Write("Q");
                    }
                    else
                    {
                        Console.Write("_");
                    }
                    if (j != BoardSize - 1)
                        Console.Write(" ");
                }
                Console.WriteLine("");
            }
            SolutionCount++;
        }
        solver.EndSearch();

        // Statistics.
        Console.WriteLine("Statistics");
        Console.WriteLine($"  failures: {solver.Failures()}");
        Console.WriteLine($"  branches: {solver.Branches()}");
        Console.WriteLine($"  wall time: {solver.WallTime()} ms");
        Console.WriteLine($"  Solutions found: {SolutionCount}");
    }
}

समाधानों की संख्या

बोर्ड के आकार के साथ सलूशन की संख्या करीब-करीब तेज़ी से बढ़ जाती है:

बोर्ड का साइज़	समाधान	सभी समाधान ढूंढ़ने में लगने वाला समय (मि॰से॰)
1	1	0
2	0	0
3	0	0
4	2	0
5	10	0
6	4	0
7	40	3
8	92	9
9	352	35
10	724	95
11	2680	378
12	14200	2198
13	73712	11628
14	365596	62427
15	2279184	410701

कई समाधान दूसरों का सिर्फ़ रोटेशन होते हैं और सिमेट्री नाम की एक तकनीक को कहते हैं कन्वर्ज़न की संख्या को कम करने के लिए, ब्रेकिंग का इस्तेमाल किया जा सकता है. हम इसका इस्तेमाल नहीं करते उसे यहां; ऊपर दिया गया हमारा समाधान तेज़ नहीं, बस आसान है. बेशक, अगर हमें हर समस्या का हल निकालना हो, तो इस काम को सभी साइज़: 50 तक के बोर्ड साइज़ के लिए, कुछ मिलीसेकंड से ज़्यादा नहीं.